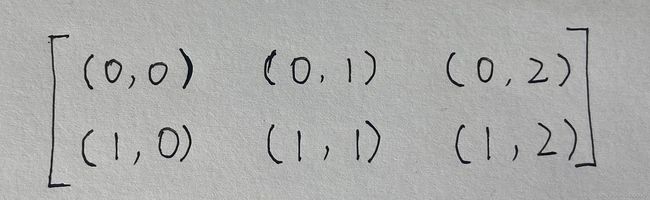np.meshgrid()函数 以及 三维空间中的坐标位置生成 以及 numpy.repeat()函数介绍
一、np.meshgrid()函数
1、np.meshgrid()介绍
X, Y = np.meshgrid(x, y) 代表的是将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的
下面是官方文档,官方文档写的也很抽象,可以不读,直接看【2、np.meshgrid()生成坐标位置】中的例子
numpy.meshgrid(*xi, copy=True, sparse=False, indexing='xy')
Return coordinate matrices from coordinate vectors.
Make N-D coordinate arrays for vectorized evaluations of N-D scalar/vector fields over N-D grids, given one-dimensional coordinate arrays x1, x2,…, xn.
2、np.meshgrid()生成坐标位置
①其实np.meshgrid()生成的并不是二维空间中的坐标,还需要把对应位置的两个值合并在一起,才是坐标位置:
例如:
import numpy as np
x = np.linspace(0, 2, 3)
y = np.linspace(0, 1, 2)
X, Y = np.meshgrid(x, y)
coors = np.concatenate((X[:, :, None], Y[:, :, None]), axis=-1)
print(X)
print(Y)
print(X[:, :, None])
print(Y[:, :, None])
print(coors)返回值:
# X
[[0. 1. 2.]
[0. 1. 2.]]
# Y
[[0. 0. 0.]
[1. 1. 1.]]
# X[:, :, None]
[[[0.]
[1.]
[2.]]
[[0.]
[1.]
[2.]]]
# Y[:, :, None]
[[[0.]
[0.]
[0.]]
[[1.]
[1.]
[1.]]]
# !!!!coors
[[[0. 0.]
[1. 0.]
[2. 0.]]
[[0. 1.]
[1. 1.]
[2. 1.]]]可以看到,np.meshgrid()生成的值,要再经过一次np.concatenate()才是坐标。
重点来了:
从上面例子的coors的输出值,可以看出:在生成坐标位置的矩阵时,是以最后一维的向量作为元素的,所以,其第-2维才是第真正的-1维,第-3维才是真正的-2维。
如下图所示:
② np.meshgrid()也可以生成三维及以上维度的坐标
import numpy as np
x = np.linspace(0, 2, 3)
y = np.linspace(0, 1, 2)
z = np.linspace(0, 3, 4)
X, Y, Z = np.meshgrid(x, y, z)
coors = np.concatenate((X[:, :, :, None], Y[:, :, :, None], Z[:, :, :, None]), axis=-1) # 注意这里是三个冒号
print(X)
print(Y)
print(Z)
print(coors)返回值:
# X
[[[0. 0. 0. 0.]
[1. 1. 1. 1.]
[2. 2. 2. 2.]]
[[0. 0. 0. 0.]
[1. 1. 1. 1.]
[2. 2. 2. 2.]]]
# Y
[[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
# Z
[[[0. 1. 2. 3.]
[0. 1. 2. 3.]
[0. 1. 2. 3.]]
[[0. 1. 2. 3.]
[0. 1. 2. 3.]
[0. 1. 2. 3.]]]
# coors
[[[[0. 0. 0.]
[0. 0. 1.]
[0. 0. 2.]
[0. 0. 3.]]
[[1. 0. 0.]
[1. 0. 1.]
[1. 0. 2.]
[1. 0. 3.]]
[[2. 0. 0.]
[2. 0. 1.]
[2. 0. 2.]
[2. 0. 3.]]]
[[[0. 1. 0.]
[0. 1. 1.]
[0. 1. 2.]
[0. 1. 3.]]
[[1. 1. 0.]
[1. 1. 1.]
[1. 1. 2.]
[1. 1. 3.]]
[[2. 1. 0.]
[2. 1. 1.]
[2. 1. 2.]
[2. 1. 3.]]]]但是,np.meshgrid()生成三维坐标位置也是有很大问题的:
无论怎么修改np.meshgrid()中x、y、z的顺序,都无法实现对x,y,z中的值都实现从小到大,而且先x从到大,然后y从小到大,最后z从小到大,见【二、1、】中例子的输出结果
二、不使用np.meshgrid()生成三维坐标位置
1、使用np.repeat()实现
numpy.repeat(a, repeats, axis=None)
Repeat elements of an array.
Parameters:
a:array_like
Input array.
repeats:int or array of ints
The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis.
axis:int, optional
The axis along which to repeat values. By default, use the flattened input array, and return a flat output array.
Returns
repeated_array:ndarray
Output array which has the same shape as a, except along the given axis.
例子:
>>> np.repeat(3, 4) array([3, 3, 3, 3]) >>> x = np.array([[1,2],[3,4]]) >>> np.repeat(x, 2) # 如果没写维度,就是flatten以后再repeat array([1, 1, 2, 2, 3, 3, 4, 4]) >>> np.repeat(x, 3, axis=1) array([[1, 1, 1, 2, 2, 2], [3, 3, 3, 4, 4, 4]]) >>> np.repeat(x, [1, 2], axis=0) # 在axis=0这个维度上,第一行重复1次,第二行重复2次 array([[1, 2], [3, 4], [3, 4]])
生成三维坐标位置:
(这个方式是我比较推荐的方式)
import numpy as np
x = np.linspace(0, 2, 3)
y = np.linspace(0, 1, 2)
z = np.linspace(0, 3, 4)
xx = np.repeat(x[None, :], len(y), axis=0) # 第一个None对应Z,第二个None对应Y;所以后面是(len(z), len(y))
xxx = np.repeat(xx[None, :, :], len(z), axis=0)
yy = np.repeat(y[:, None], len(x), axis=1)
yyy = np.repeat(yy[None, :, :], len(z), axis=0)
zz = np.repeat(z[:, None], len(y), axis=1)
zzz = np.repeat(zz[:, :, None], len(x), axis=2)
# 这里zzz, yyy, xxx的顺序别错了,不然不好理解
coors = np.concatenate((zzz[:, :, :, None], yyy[:, :, :, None], xxx[:, :, :, None]), axis=-1) # 这里zzz, yyy, xxx的顺序别错了,不然不好理解
print(coors)返回值:
[[[[0. 0. 0.]
[0. 0. 1.]
[0. 0. 2.]]
[[0. 1. 0.]
[0. 1. 1.]
[0. 1. 2.]]]
[[[1. 0. 0.]
[1. 0. 1.]
[1. 0. 2.]]
[[1. 1. 0.]
[1. 1. 1.]
[1. 1. 2.]]]
[[[2. 0. 0.]
[2. 0. 1.]
[2. 0. 2.]]
[[2. 1. 0.]
[2. 1. 1.]
[2. 1. 2.]]]
[[[3. 0. 0.]
[3. 0. 1.]
[3. 0. 2.]]
[[3. 1. 0.]
[3. 1. 1.]
[3. 1. 2.]]]]2、通过np.where()获得坐标位置
也是比较推荐的方法之一
zeros = np.zeros((4, 2, 3))
zzz, yyy, xxx = np.where(zeros==0)
print(zzz)
print(yyy)
print(xxx)
zzz = np.reshape(zzz, (4, 2, 3))
yyy = np.reshape(yyy, (4, 2, 3))
xxx = np.reshape(xxx, (4, 2, 3))
coors = np.concatenate((zzz[:, :, :, None], yyy[:, :, :, None], xxx[:, :, :, None]), axis=-1) # 这里zzz, yyy, xxx的顺序别错了,不然不好理解
print(coors)返回值:
# zzz
[0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3]
# yyy
[0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1]
# xxx
[0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2]
# coors
[[[[0 0 0]
[0 0 1]
[0 0 2]]
[[0 1 0]
[0 1 1]
[0 1 2]]]
[[[1 0 0]
[1 0 1]
[1 0 2]]
[[1 1 0]
[1 1 1]
[1 1 2]]]
[[[2 0 0]
[2 0 1]
[2 0 2]]
[[2 1 0]
[2 1 1]
[2 1 2]]]
[[[3 0 0]
[3 0 1]
[3 0 2]]
[[3 1 0]
[3 1 1]
[3 1 2]]]]