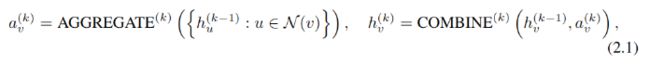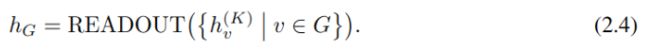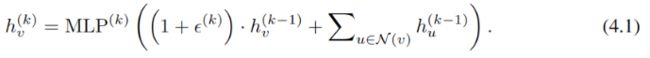论文阅读_图神经网络GIN
英文题目:How Powerful are Graph Neural Networks?
中文题目:图神经网络有多强大?
论文地址:https://arxiv.org/pdf/1810.00826.pdf
领域:图神经网络,知识表示
发表时间:2018
作者:Keyulu Xu等,MIT,斯坦福大学
出处:ICLR
被引量:1506
阅读时间:22.06.11
读后感
这也是一篇引用量很大的图神经网络精典论文。之前研究方法着重于表示节点,引文着眼于表征图的结构。作者认为之前方法难以区分不同的图结构,并提出了一种基于GNN的方法GIN,它的区分效果与WL-Test效果相当。
介绍
一般情况下一个节点的表式通过聚合它k跳之内的邻近节点计算,而全图的表示则通过对所有节点的池化计算。
近年来新型GNN的设计主要基于经验直觉、启发式和实验试错法,而对神经网络的性质和局限性的理论较少。文中提出理论框架来分析GNN的能力,这里主要是评价模型是否能够区分网络结构。
文中使用了WL-test方法,即图同构测试,它是一个区分网络结构的强效方法,也是通过迭代聚合邻居的方法来更新节点,它的强大在于使用了injective(见后)聚合更新方法。而这里要评测GNN是否能达到类似WL-test的效果。
文中还使用了多合集multiset的概念,指可能包含重复元素的集合。
论文主要贡献如下:
- 展示了GNN模型可达到与WL-test类似的图结构区分效果
- 设计了聚合函数和Readout函数,使GNN能达到更好的区分效果
- 发现GCN及GraphSAGE无法很好表达图结构,而GNN可以
- 开发了简单的网络结构GIN(图同构网络),它的区分和表示能力与WL-test类似。
预备知识
图表征
论文主要关注两种任务:一种是对图中节点的分类,通过学习节点表示,以预测节点的类别;另一种是根据图结构分类,通过学习对整个图的表示,预测整图的类别。
这里涉及节点的表示和整图的表示。各节点往往通过它的邻居节点聚合计算,通过k轮迭代后,节点的表示隐式的包含了图的结构信息。GNN第k层计算方法如下:
其中a表示聚合节点v邻近特征的方法,h是特征向量。简单说就是先聚合节点v邻居节点上一层的表示,再与节点v自身上一层的表示相结合。
算法重点在于AGGREGATE和COMBINE的具体算法。比如AGGREGATE常使用乘参数再做池化的方法,而COMBINE常使用串联方法。
对于整图分类任务,使用READOUT函数来聚合节点特征最后一次迭代的结果,生成向量来表征整个图,聚合方法也是可简可繁。
WL-test
WL-test用于比较两图的拓扑结构是否相同。
原理如图所示:(a)对于图G与G’,其中每个节点属于某种元素(标签)一共五种元素;(b)利用其邻近节点的标签组合表示当前节点;©生成新标签;(d)用新标签表示节点;依照此逻辑不断迭代。最终生成右图中的特征向量用于表征图G和G’。颜色表示标签,数值表示该标签在图中的出现次数。当两图表征不一致时,则认为两图异构。
理论框架
如图-1所示,有一个图(左图),如果想表征其中的蓝色节点,且只考虑两跳;计算方法如中图所示(子树); 通过迭代,变成了右图所示,每个节点只考虑其邻居,计算邻居时,再考虑邻居的邻居。
算法需要满足injective,injective可译为内射,即可把不同的元素映射成不同输出,在图结构中,不同的邻居结构需要生成不同的节点表征,而max,mean池化显然都不是injective的(后详述)。
建立强大的图神经网络
任何基于聚合的GNN最多与WL-test一样强大,我们要让GNN尽量逼近它,证明请见附录。
GNN公式如下:
其中f用于处理邻居节点,φ 用于内射。另外,readout也需要具有内射的性质。
除了区分不同的图之外,GNN相对于WL-test还有一个优势是它能将相似的图结构映射到相似的嵌入,并捕获图结构之间的依赖关系。而WL-test只是one-hot编码。
GIN网络
GIN网络,即图同构网络。为了在建模时实现内射,使用加和作为聚合函数,理论上多层感知机可以模拟函数的组合,用以下方法更新GIN的节点表示:
GIN的整图表征
整图分类任务,需要使用readout根据节点嵌入计算整图嵌入。计算方法如下:
用串联的方法连接了节点所有迭代步的表示,使用所有迭代是因为,随着迭代次数增加,节点能实现更加全局和精炼的表示,而早期迭代的结果则更容易泛化。
功能较弱的GNN
使用消融实验对比,展示上述公式的有效性。
单层感知机与多层感知机
单层感知机不能充分地捕获结构相似性,具体见实验结果。
平均池化和最大池化不能区分结构
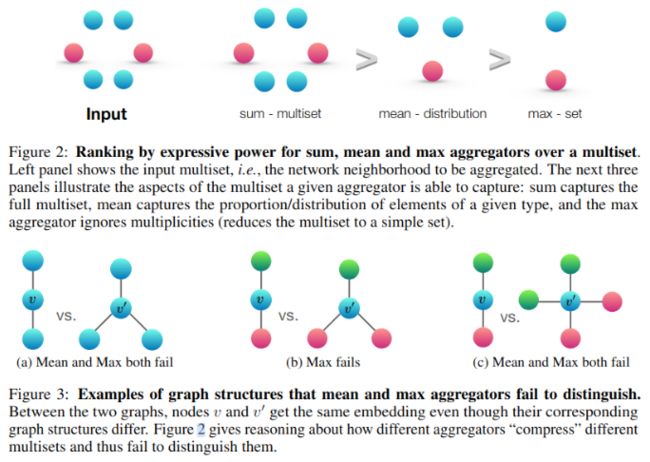
平均池化和最大池化都不是内射的,如图-2,图-3 所示:
图-2展示了在多合集情况下,sum的效果最好,mean次之,max最差。
图-3中不同颜色表示不同实体,其中图2-a中两图结构不同,但平均池化和最大池化不能加以区分,而求和可以区分;图-2b中平均池化可区分两图,但最大池化取红与绿中最大值不能区分两图;同理,使用平均池化和最大池化也不能区分图-3c中的两个图。
平均池化学习分布
平均池化不能识别某一元素出现的次数,因此,它可以捕捉实体的特征分布,但不能精确描述多合集。平均池化比较适合只看有没有,不看有多少的任务,或者特征多,重复少的任务。
最大池化学习不同元素的集合
最大池化适合捕捉具有代表性的元素或“骨架”,而不是区分确切的结构或分布的任务。
其它池化方法
还有其它池化方法,如:加权平均,LSTM池化等,而对判断同构问题来说文中使用的求和方法具有足够的表征能力。
实验
数据集
实验使用了9个数据集,其中五个生物医疗,四个社会网络,主要以捕捉结构为主。
实验结果如图-4所示: