机器学习——详解经典聚类算法Kmeans

本文始发于个人公众号：TechFlow，原创不易，求个关注

今天是机器学习专题的第12篇文章，我们一起来看下Kmeans聚类算法。

在上一篇文章当中我们讨论了KNN算法，KNN算法非常形象，通过距离公式找到最近的K个邻居，通过邻居的结果来推测当前的结果。今天我们要来看的算法同样非常直观，也是最经典的聚类算法之一，它就是Kmeans。

我们都知道，在英文当中Means是平均的意思，所以也有将它翻译成K-均值算法的。当然，含义是一样的，都是通过求均值的方式来获取样本的类簇。

既然知道Kmeans算法和均值和类簇有关，那么剩下的问题就只有两个：首先，我们应该怎么来计算均值，其次当我们获取了均值之后，又是怎么来聚类的呢？

聚类算法

上面的两个问题我们先放一放，我们先来看一个例子，假设我们有一系列用户的收入样本，我们想要将这批用户根据他们的收入、居住地以及消费情况分成富人阶级、中产阶级和工薪阶级。

在这个问题当中，我们只知道我们希望把样本分成三类，但是怎么来分，我们并不清楚，这是我们希望模型替我们完成的。也就是说我们希望模型能够自动识别这些样本之间的关联性，把关联性强的样本聚在一起，成为一个类簇。在这个问题当中，我们希望模型替我们把数据分成三个类别。

如果让我们人工来划分这个问题当然很简单，我们直接根据这些用户的收入来分。直接将用户的收入画一个折线图，然后来寻找最佳的两个切分点，三下五除二很快就搞定了。但如果我们的特征当中没有用户的收入呢？如果我们能知道用户有没有车，有没有房，家里的存款和所有外债，这就没那么直观了，不过也容易，我们简单地建模也容易解决。再如果我们连车房的信息都没有，只能拿到用户在哪里上班，用户住在哪里呢？这个问题是不是就更抽象了？

在特征比较抽象和隐晦的时候，我们想直接划分往往不太容易，由于不知道真实的标签，我们也没有办法用上监督模型。为了解决问题，Kmeans只能反其道而行之，我们不再对数据进行划分了，而让比较接近的数据自己聚集在一起。Kmeans算法正是基于这一思想而生，让数据通过某种算法聚集，不再进行划分的方法称为聚类算法。

在聚类问题当中，一系列样本被模型根据数据的属性聚合在了一起，成为了同一个类别。这里的类别就称为这些样本的类簇(cluster)。每一个簇的中心点称为簇中心。所以，KMeans算法，顾名思义，就是将样本根据用户设置的K值，一共聚类成K个类簇。

Kmeans原理

不知道大家有没有听说过这么一个理论，人类和计算机其实是相反的。一些对于人类来说困难的问题，对于计算机非常简单。比如记忆，人类很难瞬间记忆大量的东西，而计算机不是，只要带宽和容量足够，再多的数据都能记住。不但能记住，而且绝不会出错。再比如计算，人类很难快速计算复杂的公式，基本上两位数以上的乘除就必须要借助工具了。但计算机不是，只要CPU资源足够，再大量的计算都可以进行。

但是呢，人类觉得很简单的东西，对计算机来说非常困难。比如视觉，我们人类可以很轻易地分辨图片上的猫和狗，但是计算机不行。即使是深度学习和AI大行其道的今天，我们也要专门设计复杂的模型和大量数据进行训练才能让计算机学会分辨图片的内容。再比如创作，人类可以创作出前人没有的东西，计算机则不能，所谓的计算机谱曲、写作只不过是程序按照固定的模式加上一些随机波动的值综合作用的结果而已。再比如思考，人类可以思考之前从未见过的问题，计算机显然不能。

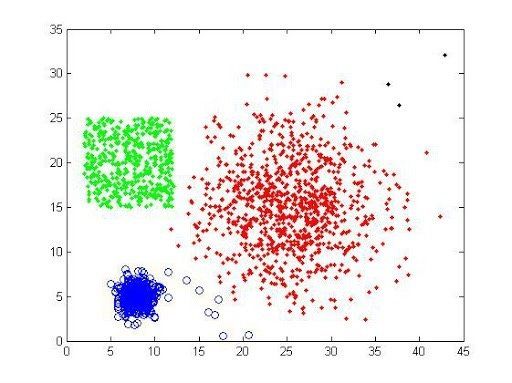
比如上图，我们人类一眼看去这是三个类别，但是计算机不行。数据在计算机当中是离散的，计算机也没有视觉，看不到数据之间的联系。所以我们看着简单的问题，其实并没有那么简单，但其实刚才的分析当中我们已经道出了本质：既然计算机看不到联系，那么我们就要想办法让它能够“看到”，说看到应该不够准确，准确地说是算到。

回想一下，我们刚才是怎么快速分辨出图上有三个类别的？你会说很简单嘛，因为三个区域内点最多啊。这个说法很正确，但是不够量化，如果我们量化一下，应该是存在三个区域密度最大。一旦量化表达以后，问题就清楚了，我们正是要通过密度来进行聚类。Kmeans正是基于这一朴素的思想，但是它过于朴素，并没有设计计算类簇数量的算法，所以这个类别数量K，是要用户提供的。

也就是说算法并不知道要聚成几类，我们说是几类就是几类。

我们忽略这一细节，假设我们通过某种奇怪的方法知道了数据一共分成三类，那么Kmeans怎么进行划分呢？

我们深入思考会发现我们虽然说是要量化密度，但是密度很难量化。因为密度的定义本身就是基于聚类之后的结果的，我们肯定是已经知道了这样一批数据聚集在了一起才能算它们的密度，而不是相反。所以这个思路是靠谱的，但是直接这么做是不行的。但是直接做不行，不意味着倒着不可以，这个思路在数学上很常见，在这里我们又遇到了。

既然我们通过密度来聚类不行，那么我们能不能先聚类再算密度，根据密度的结果调整呢？

我Google了好久也没找到Kmeans原作者的信息，但我想能想出这么天才想法的人，他一定很机智。Kmeans正是基于这么朴素又机智的思路衍生的。

初始化

在算法运行的伊始，Kmeans会在数据集的范围当中随机选择K个中心点，然后依据这K个中心点进行聚类。中心点有了聚类其实很容易，对于每一个样本来说我们只需要计算一下它和所有中心的距离，选择最近的那个就好了。

当然，这样得到的结果肯定很不准，但是没关系，即使依据不靠谱的中心，我们也可以完成聚类，我们把随机到的中心点的位置和最后的聚类结果都画在一张图上，可以看到虽然一开始选的位置看起来不是那么靠谱，但是我们一样可以达成一个不错的结果。

初始的聚类结果肯定是不准的，但是没有关系，我们不怕不准，就怕没有结果。有了结果就好办了，我们可以针对这个结果进行分析来查看优化的方向。有了优化的方向就可以让结果变得越来越准，就好像在线性回归当中，我们也不是第一下就搞定最佳参数的选值的，也是通过梯度下降一点一点迭代出来的。

迭代

在我们介绍具体的迭代方法之前，先来分析下情况。显然由于随机选取的关系，聚类的结果肯定是不准的，不准的原因是由于我们随机选取的中心和类簇距离太远导致的。也就是说我们要想办法让中心向着类簇靠近。

那怎么才能靠近呢，我们先来看一下完美聚类之后的情况。

我们来观察一下，完美聚类时中心点和类簇重叠。那么这个中心点有什么性质呢？如果对物理熟悉的话，应该能联想到，这个中心点应该是这个类样本的质心。即使不熟悉这个概念也没关系，我们通过上图可以观察出来，样本点均匀地分散在中心的四周。均匀地分散会有一个什么特点？也容易想到，就是出现在中心点左侧和右侧，上侧和下侧，以及其他各个方向上的点数量和分布都差不多。我们量化一下这个概念，可以得到类别当中所有点的坐标均值就是中心点的位置。

那么问题来了，在一个聚类错误的情况下，样本坐标的均值（即质心）和我们选取的中心点会重合吗？如果不重合会有怎样的偏差呢？

我们从上图其实可以猜出来，由于我们选的中心点位置不对，所以它和聚类之后样本的质心肯定是不重合的。两者偏差的方向，就是它距离质心的方向。

这个结论也很朴素，因为距离真实的类簇越近，点越密集，那么算出来的质心显然会更靠近真实类簇的方向。有了这个结论，就很简单了，我们只要每次聚类之后计算一下各个类的质心，然后将算出来的质心作为下一次聚类的中心点重新聚类，一直重复上面的过程就行了。当聚类之前的中心和聚类之后的质心重叠的时候，就说明聚类收敛，我们找到了类簇。

下图展现了一个类别中心随着迭代而变化的情况，我们可以很直观地看到，随着我们的迭代，我们的类中心距离真正的簇中心越来越近，经过了三次迭代，就已经非常接近最后的结果了。所以这个结论是正确的，用质心来作为新的中心来迭代的思路是可行的。

代码实现

Kmeans的原理以及牵引侯贵搞清楚了之后，用Python实现就变得很简单了。

我们当然可以自己编写生成数据的逻辑，但sklearn库当中为我们提供了创造数据的API，通过调用API我们可以很轻松地创造我们想要的数据。我们可以使用dataset.make_blobs创造聚类数据。传入样本的数量和特征的数量，真实类簇的坐标以及样本的标准差，就可以得到一批相应的样本。

def createData():
    X, y = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1],[1,1],[2,2]], cluster_std=[0.2,0.3,0.4])
    return X, y

创建完数据之后，下面我们就可以开始算法的实现了。

首先，我们先开发整个算法的基础方法，来简化后续的开发。在KMeans问题当中，我们已经知道我们是通过向量和各类簇中心在样本空间的距离来调整样本的所属类别。所以，我们先开发向量之间距离的计算方法。

使用numpy，整个的计算过程会变得非常简单：

def calculateDistance(vecA, vecB):
    return np.sqrt(np.sum(np.square(vecA - vecB)))

在这一行代码当中，我们先计算了两个向量的差向量。然后我们对这个差向量的每一项求平方和再开方，这样就得到了向量A和B的欧氏距离。

接着，我们需要随机K个类簇的中心点的坐标。虽然在KMeans算法当中类簇的选择是随机的，但是需要注意的是，我们的随机的范围并不是无限的。因为聚类是为了寻找样本密集度最高的K个位置，没有样本分布的地方自然也是不可能找到合法的类簇的。所以我们可以将随机的范围限制在样本的分布范围内，这样可以大大简化计算量。

def randomCenter(samples, K):
    m,n = np.shape(samples)
    centers = np.mat(np.zeros((K, n)))
    for i in range(n):
		    # 通过np.max获取i列最大值
        mxi = np.max(samples[:, i])
		    # 通过np.min获取i列最小值
        mni = np.min(samples[:, i])
        rangeI = mxi - mni
		    # 为簇中心第i列赋值
        centers[:, i] = np.mat(mni + rangeI * np.random.rand(K, 1))
    return centers

上面的逻辑不难理解，我们首先为K个簇中心创建坐标矩阵并初始化为0，这里的n是样本的维度数。接着，我们遍历这n个维度，查找样本当中每个维度的最大值和最小值。有了这两个值，我们就知道了簇中心在每个样本维度上的取值范围。最后，我们再调用random.rand方法随机出具体的坐标即可。

到这里，算法需要的两个基本工具都已经开发完了。接下来只要实现迭代的流程，整个KMeans就算是完成了。

在我们继续往下开发之前，我们先来测试一下我们开发好的这两个接口。

首先，我们先生成数据：

看到有数据产出，说明我们的数据已经生成好了，接下来根据生成的数据，随机选出K个簇中心。

我们在生成数据的时候传入的样本中心点有三个，所以簇中心数量就是3，也就是说我们的K就是3，那么我们接着调用randomCenter方法，查看结果。

果然，我们生成了3个点。为了保险，我们需要输出样本的范围，检查我们生成的点的坐标是否在我们样本的范围当中。

使用numpy的max和min方法，结合Python语言的切片操作，我们可以非常方便地求解这四个值。很明显，我们的簇中心都在范围当中。我们的代码没有问题。

这两个方法没问题之后，我们就可以着手开发KMeans的核心逻辑了，也就是聚类的计算逻辑。

根据我们之前列出来的伪代码，我们先随机出簇中心。然后根据簇中心给各个样本标记上类别。最后再根据标记好的样本更新簇中心的位置，整个逻辑其实非常简单，写成代码也不复杂：

def KMeans(dataset, k):
    m, n = np.shape(dataset)
    # 最后的返回结果，一共两维，第一维是所属类别，第二维是到簇中心的距离
    clusterPos = np.zeros((m, 2))
    
    centers = randCenter(dataset, k)
    clusterChange = True
    while clusterChange:
        clusterChange = False
        # 遍历所有样本
        for i in range(m):
            minD = inf
            idx = -1
            # 遍历到各个簇中心的距离
            for j in range(k):
                dis = calculateDistance(centers[j,:], dataset[i, :])
                if dis < minD:
                    minD = dis
                    idx = j
            # 如果所属类别发生变化
            if clusterPos[i,0] != idx:
                clusterChange = True
            # 更新样本聚类结果
            clusterPos[i,:] = idx, minD
        # 更新簇中心的坐标
        for i in range(k):
            nxtClust = dataset[np.nonzero(clusterPos[:,0] == i)[0]]
            centers[i,:] = np.mean(nxtClust, axis=0)
    return centers, clusterPos

下面，我们来测试一下我们的代码，看看能不能聚类出正确的结果。

centers, clusterRet = KMeans(x, 3)
plt.scatter(x[:,0],x[:,1],c=clusterRet[:,0] ,s=3,marker='o')
plt.scatter(centers[:, 0].A, centers[:, 1].A, c='red', s=100, marker='x')
plt.show()

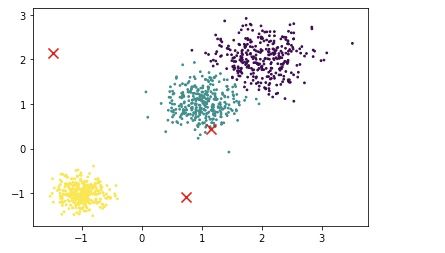
我们把样本当中的所有点根据聚类之后的结果进行绘制，再在同一张图上标记出簇中心的位置，得到的结果如下。

不难看出，在上图当中，无论是簇中心的位置还是最后的聚类结果，基本上和我们人工估计的结果一样。说明我们写的KMeans算法成功运行，并输出了正确的结果。

总结

到这里，关于Kmeans算法的原理和代码就都介绍完了。不知道大家有什么感觉，我当时初学这个算法的时候，最大的感受就是简单，这个算法也太“儿戏”了，理解起来也很容易，没有什么弯弯绕或者是复杂的东西，所有问题和思路都直来直去。

算法简单我们学习起来就容易，但是往往太简单的算法都会留下短板。Kmeans的短板也很明显，相信大家也都感受到了。我们每次迭代的时候，都需要对所有的样本计算所属的类别，这可是一次全量的计算。而由于我们初始的中心点是随机选取的，这也导致了一开始中心的位置和最后的类簇可能相去甚远，距离越远显然需要的迭代次数也就越多，那么带来的计算消耗自然也就越大。

那么，针对kmeans效率的问题有没有什么提升的方法呢？

大家可以先思考一下这个问题，我将会在下周的机器学习专题当中和大家讨论相关内容。

同样，由于Kmeans算法原理简单，实现容易，所以它经常出现在各大公司的招聘笔试题当中。据我所知，阿里巴巴有好几年的笔试题就是让选手手写一个kmeans聚类。所以虽然这个算法简单，但是我们也不能掉以轻心。另外，对于算法也不能满足于了解原理，凡事可以多想一想多问一问，这样理解才更加深入，以后应对面试才更加灵活。

今天的文章就是这些，如果觉得有所收获，请顺手点个关注或者转发吧，你们的举手之劳对我来说很重要。