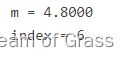【数模】选址问题 7个居民点中建设银行(多目标,NP-Hard)
选址问题
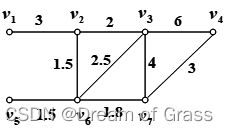
现准备在7个居民点中设置一银行,路线与距离如下图,问设在哪个点,可使最大服务距离最小?若设两个点呢?
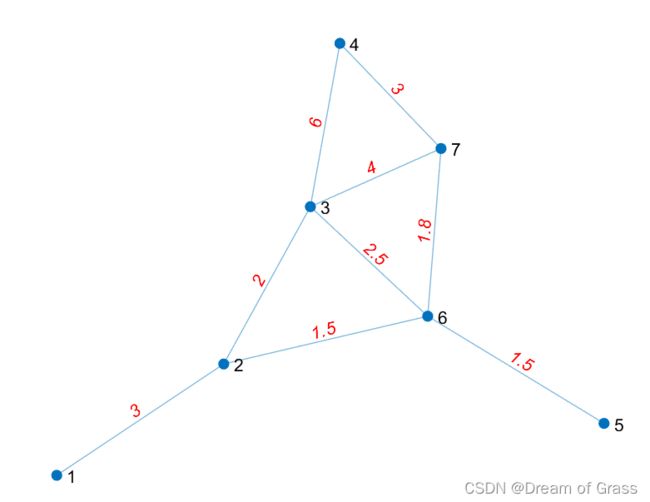
在matlab中把图给画出来
s = [1 2 2 3 3 3 4 5 6];
t = [2 3 6 4 6 7 7 6 7];
weights = [3 2 1.5 6 2.5 4 3 1.5 1.8];
G = graph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight,"EdgeLabelColor",'r')
算出每个点到其他点的最小加权距离
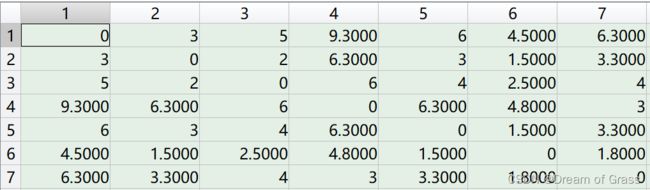
总共有7个节点,算出每个点到其他点最短加权路径之和,最终得到一个对称的矩阵,其中每个点表示i到j的距离。
% 总共有7个节点
% 算出每个点到其他点最短加权路径之和
% 最终得到一个对称的矩阵,其中每个点表示i到j的距离
D=zeros(7,7);
for i=1:7
for j=1:7
[ ~,D(i,j)] = shortestpath(G,i,j);
end
end
计算每个点作为银行建设点的最大服务距离
% 看看哪个覆盖范围最大
[m,index]=min(max(D'))
最后结果是6号点,最大服务距离为4.8
第二问
第二问要求建两个银行,主要思想就是,把所有建银行的可能情况都列出来,然后计算,每个点到这两个银行距离的最小值作为该点到银行的距离,之后把这些距离的最大值作为该店建银行的最大服务距离,最后找到这些最大服务距离的最小值即可得到结果。
列出所有的选两个点的情况
% 第二问
% 列出所有的选两个点的情况
tp=zeros(21,11);
tt=1;
for i=1:7
for j=i+1:7
tp(tt,1)=i;
tp(tt,2)=j;
tt=tt+1;
end
end
| 点1 | 点2 |
|---|---|
| 1 | 2 |
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 1 | 6 |
| 1 | 7 |
| 2 | 3 |
| 2 | 4 |
| 2 | 5 |
| 2 | 6 |
| 2 | 7 |
| 3 | 4 |
| 3 | 5 |
| 3 | 6 |
| 3 | 7 |
| 4 | 5 |
| 4 | 6 |
| 4 | 7 |
| 5 | 6 |
| 5 | 7 |
| 6 | 7 |
D2=zeros(7,1);
for i=1:length(tp)
for j=1:7
[ ~,temp1] = shortestpath(G,j,tp(i,1));
[ ~,temp2] = shortestpath(G,j,tp(i,2));
tp(i,j+2) = min([temp1 temp2]);
end
end
tp(:,10) = sum(tp(:,3:9),2);
tp(:,11) = max(tp(:,3:9),[],2);
% [m,index]=min(tp(:,11))
% 因为会有多个最小的,故用find函数找
res=tp(find(tp(:,11)==min(tp(:,11))),1:2)
最终结果是在2、4或者2、7建银行。
变题
这个题目是让我们求设在哪个点,可使最大服务距离最小,其实,如果把问题改成设在哪个点,可使其他点离银行的总距离最小。
思路
思路其实很简单,就是在之前的基础上,把每个点到银行的距离加起来,然后找到建银行距离总和最小的点。
变题第一问
最后看看哪个点的路径之和最小
[m,index]=min(sum(D))
最后结果也是6号点,距离其他点的总距离是16.6
变题第二问
D2=zeros(7,1);
for i=1:length(tp)
for j=1:7
[ ~,temp1] = shortestpath(G,j,tp(i,1));
[ ~,temp2] = shortestpath(G,j,tp(i,2));
tp(i,j+2) = min([temp1 temp2]);
end
end
tp(:,10) = sum(tp(:,3:9),2);
tp(:,11) = max(tp(:,3:9),[],2);
% [m,index]=min(tp(:,11))
% 因为会有多个最小的,故用find函数找
res=tp(find(tp(:,11)==min(tp(:,11))),1:2)
res2=tp(find(tp(:,10)==min(tp(:,10))),1:2)
最后结果是在4、6建银行会让总距离最小。
结语
由此可见,让最大服务距离最小的时候不一定总距离会最小。
下表是问题2的总结果
| 第一个点 | 第二个点 | 点1距银行的距离 | 点2距银行的距离 | 点3距银行的距离 | 点4距银行的距离 | 点5距银行的距离 | 点6距银行的距离 | 点7距银行的距离 | 距离之和 | 最大距离 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 0 | 2 | 6.3 | 3 | 1.5 | 3.3 | 16.1 | 6.3 |
| 1 | 3 | 0 | 2 | 0 | 6 | 4 | 2.5 | 4 | 18.5 | 6 |
| 1 | 4 | 0 | 3 | 5 | 0 | 6 | 4.5 | 3 | 21.5 | 6 |
| 1 | 5 | 0 | 3 | 4 | 6.3 | 0 | 1.5 | 3.3 | 18.1 | 6.3 |
| 1 | 6 | 0 | 1.5 | 2.5 | 4.8 | 1.5 | 0 | 1.8 | 12.1 | 4.8 |
| 1 | 7 | 0 | 3 | 4 | 3 | 3.3 | 1.8 | 0 | 15.1 | 4 |
| 2 | 3 | 3 | 0 | 0 | 6 | 3 | 1.5 | 3.3 | 16.8 | 6 |
| 2 | 4 | 3 | 0 | 2 | 0 | 3 | 1.5 | 3 | 12.5 | 3 |
| 2 | 5 | 3 | 0 | 2 | 6.3 | 0 | 1.5 | 3.3 | 16.1 | 6.3 |
| 2 | 6 | 3 | 0 | 2 | 4.8 | 1.5 | 0 | 1.8 | 13.1 | 4.8 |
| 2 | 7 | 3 | 0 | 2 | 3 | 3 | 1.5 | 0 | 12.5 | 3 |
| 3 | 4 | 5 | 2 | 0 | 0 | 4 | 2.5 | 3 | 16.5 | 5 |
| 3 | 5 | 5 | 2 | 0 | 6 | 0 | 1.5 | 3.3 | 17.8 | 6 |
| 3 | 6 | 4.5 | 1.5 | 0 | 4.8 | 1.5 | 0 | 1.8 | 14.1 | 4.8 |
| 3 | 7 | 5 | 2 | 0 | 3 | 3.3 | 1.8 | 0 | 15.1 | 5 |
| 4 | 5 | 6 | 3 | 4 | 0 | 0 | 1.5 | 3 | 17.5 | 6 |
| 4 | 6 | 4.5 | 1.5 | 2.5 | 0 | 1.5 | 0 | 1.8 | 11.8 | 4.5 |
| 4 | 7 | 6.3 | 3.3 | 4 | 0 | 3.3 | 1.8 | 0 | 18.7 | 6.3 |
| 5 | 6 | 4.5 | 1.5 | 2.5 | 4.8 | 0 | 0 | 1.8 | 15.1 | 4.8 |
| 5 | 7 | 6 | 3 | 4 | 3 | 0 | 1.5 | 0 | 17.5 | 6 |
| 6 | 7 | 4.5 | 1.5 | 2.5 | 3 | 1.5 | 0 | 0 | 13 | 4.5 |