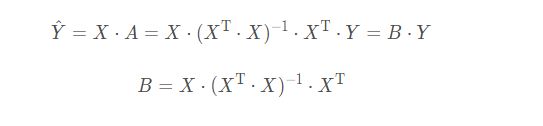文献阅读(SG滤波器—(LSTM)编码器与解码器模型,预测水质)—OrdinaryKriging模型
文章目录
- 摘要
- 一.Large-scale water quality prediction with integrated deep neural network(基于集成深度神经网络的大规模水质预测)
-
- 1.1 论文摘要
- 1.2 问题描述
- 1.3 模型设计
-
- 1.3.1 SG filter
- 1.3.2 SE-LSTM
- 1.4 评估标准
- 1.5 实验特点
- 1.6 思考点
- 补充点(SG滤波器的原理)
- 二. 深度学习方面
- 三. 工程项目
- 四. 本科毕设
摘要
本周一是阅读了基于集成深度神经网络的大规模水质预测的论文,其首先是应用SG滤波器去实现水质数据平滑去噪,再将预处理后的数据,输入给基于LSTM的编码器-解码器神经网络模型去提取水质数据的特征,。对SG滤波器的原理的理解与基于python简单实现SG滤波器的平滑去噪处理,并在滤除噪声的同时可以确保信号的形状、宽度不变。
二是对用OrdinaryKriging模型,去简单实现克里金的空间插值。
文献阅读
一.Large-scale water quality prediction with integrated deep neural network(基于集成深度神经网络的大规模水质预测)
作者:Jing Bi, Yongze Lin, Quanxi Dong, Haitao Yuan.
参与单位:北京工业大学信息技术学院软件工程学院
中国北京航空航天大学自动化科学与电气工程学院
中国电子与计算机工程系,新泽西理工学院(2021.4.11日最终版)
1.1 论文摘要
水环境时间序列预测是水资源有效管理的重要内容。传统的水质预测主要基于线性模型。然而,由于水环境条件复杂,水质时间序列中存在大量噪声,严重影响水质预测的准确性。另外,线性模型难以处理时间序列数据的非线性关系。为了应对这一挑战,本文提出了一种基于长-短记忆编码-解码神经网络和Savitzky-Golay滤波器的混合模型。其中,Savitzky-Golay滤波器可以消除水质时间序列中的潜在噪声,长-短记忆可以研究复杂水环境中的非线性特征。通过这种方式,提出了一个综合模型,有效地获得了统计特征。基于真实数据的实验证明,它的预测性能优于几种最先进的同行。
1.2 问题描述
为了精准预测DO(溶氧量)与CODMN(化学需要量)等重要水质指标,改善水环境的管理。各种水质指标往往随时间动态变化。准确的水质预测可以帮助水环境管理部门做出决策,从而确保水质值在合理范围内。预测方法:从线性方法(ARIMA,MA)等,到(SVM,ANN,auto-encode,BPNN )等非线性方法,或者有线性与非线性方法的组合。本文引入LSTM可以更好的捕获水质数据的特征,并由于数据中存在噪声,预测模型往往存在过度拟合问题。Savitzky-Golay(SG)滤波器(过滤掉不想要的信号波,杂波)可以减少时间序列的噪声干扰,提高上述模型的预测精度。
-
Li等人结合LSTM和稀疏自动编码器设计了一种混合预测模型。由稀疏自动编码器预训练的隐藏层中的数据包含水质的潜在特征。该深度模型有效地提高了多步预测的精度。Dong等人采用基本的LSTM模型来预测水质。Bi等人采用注意机制来预测水质。然而,这些模型未能改善LSTM的网络结构。与上述模型不同,我们提出的模型改进了编解码网络结构,使其更好地适应多步时间序列预测。同时,为了解决时间序列数据的降噪问题,本文采用SG滤波器对原始数据进行去噪。
-
本文设计了一个基于LSTM的编码器-解码器神经网络和SG滤波器(SELSTM)的混合模型来预测未来的水质。(SG滤波器可以在去除噪声的同时有效地保留时间序列的特性)
1.3 模型设计
1.3.1 SG filter
为了消除水质的频繁变化,我们使用SG过滤器来减少噪声的干扰。该滤波器在去噪过程中保留了数据的有效信息。然后,通过线性最小二乘法对每个数据子序列进行拟合。
1.3.2 SE-LSTM
为了获得更好的预测精度,本工作提出了一种新的编码器-解码器神经网络,其结构如图:

训练模型:
输入:水质序列{ x 1 ; x 2 ; . . . ; x T x_1;x_2;...;x_T x1;x2;...;xT}
输出:预测序列{ y 1 ; y 2 ; . . . ; y 涛 t y_1;y_2;...;y_涛t y1;y2;...;y涛t}
- 初始化窗口大小(m)、多项式次数(k)、学习速率:(lr)、输入步数(T)、(多步预测)预测步数(涛t)、隐藏状态(p=q)。
- ️ℭ从1到T:
- 如上述SG滤波器公式,获取到滤波后的数据序列。
- 对于每一次迭代:
- t 从1到T:
- 输入 x t x_t xt和 h ( t − 1 ) h_(t - 1) h(t−1),通过(6)-(9)中LSTM的编码器生成 h t h_t ht和 c t c_t ct.(直到最后)
- t’从1到 涛t:(涛t为预测步长)
- 输入 c T c_T cT和 d ( t ′ − 1 ) d_(t'-1) d(t′−1),通过(6)-(9)中的LSTM的解码器生成,得出 d ( t ′ ) d_(t') d(t′),并生成 y t ′ y'_t yt′.(直到最后)
- 根据损失函数计算Loss
- 应用BPTT反向传播梯度
- 用Adam优化器对模型进行最小化损失训练
1.4 评估标准
为了证明SE-LSTM的预测性能,采用三个指标来评价其预测精度。
三个评估标准公式如下:
1.5 实验特点
数据来源:
水环境实验数据集采集自中国北京市古北口。该数据每4小时收集一次,从2014年4月到2018年10月共收集了超过1万条数据。然后,数据集被分成两个部分,包括训练集和测试集,比例为9:1。所有预测模型均采用DO和CODMn作为实验数据。
- 对数据预处理,采用SG滤波器平滑处理数据,并通过实验与MM、SG和MA过滤器得出最佳滤波器是SG,计算实验(均方根误差)RSME的大小,选出最合适的窗口大小。
- 为了获得更好的SG滤波器,我们给出了不同的参数设置,通过实验结果对比,设置窗口大小m与多项式K次的大小值;过大的窗口大小会去除时间特征,而过小的窗口大小则不能用来减少噪声。同样,太大K会导致最小二乘的过拟合,太小K会导致拟合不足。
- 本实验在超参数的设置上,也是设计的较为科学合理,如m,k,的设置与特别是在输入时间步长T,隐藏状态p=q,的设置上,都是通过实验对比。
- 为了更好地评价模型的多步预测,本实验将预测步长(涛t)从1到5,分别在不同的模型下,不同的预测步长下,进行对比分析,发现LSTM和SE-LSTM在多步拟合中的表现更优。
- 从线性方法,到传统神经网络模型,到深度学习LSTM等,都一一详尽的做了实验对比,此外,加入SG滤波器后,所有模型的预测精度都得到了显著提高,从而更有道理的论述了该SE-LSTM模型的独特之处。
1.6 思考点
- 采用Savitzky-Golay滤波器对时间序列数据进行滤波,另外本文采用基于LSTM的编码器-解码器模型来捕获特征。实验结果表明,该模型比现有的一些基准模型具有更高的预测精度。
- 可以扩展模型从一下两点:一是研究相关的降维算法,通过一些平滑方法来减少相关噪声的干扰,更好地提取时间特征;二是进一步改进现有模型的网络结构,使其不仅可以接收历史数据,还可以捕获相关多特征数据的输入。
- 我们可以将该模型应用到其他领域,例如:金融时间序列和交通流,以验证其有效性和稳健性。
- 可以将图神经网络与时间序列模型相结合,提取水质时空特征。
补充点(SG滤波器的原理)
简介:
1 . Savitzky-Golay平滑滤波是光谱预处理中常用滤波方法,它的核心思想:是对一定长度窗口内的数据点进行k阶多项式拟合,从而得到拟合后的结果。 对它进行离散化处理后后,S-G 滤波其实是一种移动窗口的加权平均算法,但是其加权系数不是简单的常数窗口,而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。
2 . Savitzky-Golay平滑滤波被广泛地运用于数据流平滑除噪,是一种在时域内基于局域多项式最小二乘法拟合的滤波方法。这种滤波器最大的特点在于在滤除噪声的同时可以确保信号的形状、宽度不变。
3 . 用平滑滤波器对信号滤波时,实际上是拟合了信号中的低频成分,而将高频成分平滑出去了。 如果噪声在高频端,那么滤波的结果就是去除了噪声,反之,若噪声在低频段,那么滤波的结果就是留下了噪声。
公式推导:
设滤波窗口的宽度为 n = 2 m + 1 n=2m+1 n=2m+1,各测量点为 x = ( − m , − m + 1 , ⋯ , 0 , 1 , ⋯ , m − 1 , m ) x=(-m, -m+1, \cdots, 0, 1, \cdots, m-1, m ) x=(−m,−m+1,⋯,0,1,⋯,m−1,m),采用 k − 1 k−1 k−1 次多项式对窗口内的数据点进行拟合:
y = a 0 + a 1 x + a 2 x 2 + ⋯ + a k − 1 x k − 1 y = a_0 + a_1 x + a_2 x^2 + \cdots + a_{k-1} x^{k-1} y=a0+a1x+a2x2+⋯+ak−1xk−1
于是就有了 n n n 个这样的方程,构成了 k k k 元线性方程组。要使方程组有解则 n n n 应大于等于 k k k,一般选择 n > k n>k n>k,通过最小二乘法拟合确定拟合参数 A A A。由此可得到:

上述公式可能过于复杂不方便理解,我们假设一个五点三次平滑公式,即 m = 2 m = 2 m=2 , n = 2 ∗ 2 + 1 = 5 n = 2 ∗ 2 + 1 = 5 n=2∗2+1=5 , k = 3 k = 3 k=3 ,代入公式:

转换成矩阵表示的形式为:
Y ( 2 m + 1 ) × 1 Y_(2m+1)×1 Y(2m+1)×1 = X ( 2 m + 1 ) × k X _(2m+1)×k X(2m+1)×k ⋅ A ( k × 1 ) A_ (k×1) A(k×1)+ E ( 2 m + 1 ) × 1 E _(2m+1)×1 E(2m+1)×1
A 的最小二乘解 A − A^- A− 为:
A − = ( X T ⋅ X ) − 1 ⋅ X T ⋅ Y A^-=(X ^T⋅X)-1⋅X^ T⋅Y A−=(XT⋅X)−1⋅XT⋅Y
Savitzky-Golay 滤波器代码实现曲线平滑
python中Savitzky-Golay滤波器调用如下:
两种调用方法
y_smooth = scipy.signal.savgol_filter(y,53,3)
# 或者
y_smooth2 = savgol_filter(y, 99, 1, mode= 'nearest')
# 注意:
y:代表曲线点坐标(x,y)中的y值数组
window_length:窗口长度,该值需为正奇整数。例如:此处取值53
k值:polyorder为对窗口内的数据点进行k阶多项式拟合,k的值需要小于window_length。例如:此处取值3
**mode**:确定了要应用滤波器的填充信号的扩展类型。(This determines the type of extension to use for the padded signal to which the filter is applied. )
实现平滑数据简单案例:
import numpy as np
import matplotlib.pyplot as plt
Size = 100
x = np.linspace(1, Size, Size)
data = np.random.randint(1, Size, Size)
print(data)
# >> >
# array([97 78 27 7 83 97 70 64 92 53 28 21 36 97 68 67 72 73 22 57 70 61 93 75
# 76 59 51 17 43 97 92 84 43 70 92 16 59 10 64 60 7 12 42 65 23 14 12 40
# 66 49 77 17 19 93 70 72 36 69 71 44 67 70 64 79 31 9 88 3 64 67 64 58
# 52 20 97 73 72 15 18 60 36 50 83 47 10 6 15 55 76 72 66 88 68 64 18 72
# 60 92 56 21])
# 可视化图线
plt.plot(x, data)
#plt.show()
# 使用Savitzky-Golay 滤波器后得到平滑图线
from scipy.signal import savgol_filter
y = savgol_filter(data, 5, 3, mode='nearest')
# 可视化图线
plot1 = plt.plot(x, data, 'b', label='original values')
plot2=plt.plot(x, y, 'r', label='savgol')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.show()
效果图展示:

注:blue为原始数据,red为SG滤波器平滑去噪后数据。
(1)window_length对曲线的平滑作用: window_length的值越小,曲线越贴近真实曲线;window_length值越大,平滑效果越厉害(备注:该值必须为正奇整数)。
(2)k值对曲线的平滑作用: k值越大,曲线越贴近真实曲线;k值越小,曲线平滑越厉害。另外,当k值较大时,受窗口长度限制,拟合会出现问题,高频曲线会变成直线。
二. 深度学习方面
本周只是看了基于python下载克里金插值函数包pykrige,并没有详细拆开,只是直接利用OrdinaryKriging模型,去简单实现克里金的空间插值。
from pykrige.ok import OrdinaryKriging
import numpy as np
from matplotlib import pyplot as plt
import xlrd #读取excel的库
# 已知采样点的数据,是坐标(x,y)和坐标对应的值
# 矩阵中第一列是x,第二列是y,第三列是坐标对应的值
# data 样例格式
# data = np.array(
# [
# [0.1, 0.1, 0.9],
# [0.2, 0.1, 0.8],
# [0.1, 0.3, 0.9],
# [0.5, 0.4, 0.5],
# [0.3, 0.3, 0.7],
# ])
resArray=[] # 先声明一个空list
data = xlrd.open_workbook("guiyihua.xlsx") #读取文件
table = data.sheet_by_index(0) # 按索引获取工作表,0就是工作表1
for i in range(table.nrows): # table.nrows表示总行数
line=table.row_values(i) # 读取每行数据,保存在line里面,line是list
resArray.append(line) # 将line加入到resArray中,resArray是二维list
resArray=np.array(resArray) # 将resArray从二维list变成数组
# a = np.squeeze(resArray, 0)
# print(a)
# 绘图 网格
x_range = 1.0
y_range = 1.0
range_step = 0.1 # 步长
gridx = np.arange(0.0, x_range, range_step) #三个参数的意思:范围0.0 - 1.0 ,每隔0.1划分一个网格
gridy = np.arange(0.0, y_range, range_step)
ok3d = OrdinaryKriging(resArray[:, 0], resArray[:, 1], resArray[:, 2], variogram_model="linear") # 模型
# variogram_model 是变差函数模型
# pykrige提供 linear, power, gaussian, spherical, exponential, hole-effect
# 几种variogram_model可供选择,默认的为linear模型
# 使用不同的variogram_model,预测效果是不一样的,应该针对自己的任务选择合适的variogram_model
k3d1, ss3d = ok3d.execute("grid", gridx, gridy) # k3d1是结果,给出了每个网格点处对应的值
print(np.round(k3d1,2))
#输出的结果
# [[21.34 21.25 21.17 21.1 21.04 20.96 20.84 20.71 20.56 20.43]
# [21.38 21.28 21.18 21.09 21.03 20.98 20.9 20.7 20.51 20.35]
# [21.43 21.32 21.2 21.06 21.01 21.0 20.9 20.68 20.42 20.25]
# [21.5 21.38 21.25 21.14 21.08 21.04 20.93 20.66 20.32 20.09]
# [21.58 21.46 21.33 21.21 21.22 21.11 20.95 20.64 20.25 19.98]
# [21.69 21.57 21.41 21.26 21.22 21.05 20.83 20.51 20.15 19.93]
# [21.83 21.72 21.56 21.39 21.24 21.07 20.81 20.44 20.13 20.01]
# [21.96 21.88 21.74 21.57 21.46 21.26 20.9 20.51 20.2 20.06]
# [22.08 21.97 21.82 21.66 21.5 21.3 21.0 20.69 20.4 20.16]
# [22.07 21.97 21.83 21.68 21.51 21.31 21.07 20.83 20.58 20.25]]
# 绘图
fig, (ax1) = plt.subplots(1)
ax1.imshow(k3d1, origin="lower")
ax1.set_title("ordinary kriging")
plt.tight_layout()
plt.show()
1.接下来计划将包解开详细看,对照数学公式,理解背后机制;对其中的半方差函数应该是怎样去拟合的,网络该如何去替换。目前还是不清楚。
2.快速学习python数据分析工具,以及pytorch框架的各模型的搭建,跑通经典模型。
三. 工程项目
无
四. 本科毕设
指导学弟完成了开题报告,以及准备开题答辩工作。