【时序】LSTNet：结合 CNN、RNN 以及 AR 的时间序列预测模型

论文名称：Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks
论文下载：https://dl.acm.org/doi/abs/10.1145/3209978.3210006
论文年份：SIGIR 2018
论文被引：594（2022/04/21）
论文代码：https://github.com/laiguokun/LSTNet
论文数据：https://github.com/laiguokun/multivariate-time-series-data

ABSTRACT

Multivariate time series forecasting is an important machine learning problem across many domains, including predictions of solar plant energy output, electricity consumption, and traffic jam situation. Temporal data arise in these real-world applications often involves a mixture of long-term and short-term patterns, for which traditional approaches such as Autoregressive models and Gaussian Process may fail. In this paper, we proposed a novel deep learning framework, namely Long- and Short-term Time-series network (LSTNet), to address this open challenge. LSTNet uses the Convolution Neural Network (CNN) and the Recurrent Neural Network (RNN) to extract short-term local dependency patterns among variables and to discover long-term patterns for time series trends. Furthermore, we leverage traditional autoregressive model to tackle the scale insensitive problem of the neural network model. In our evaluation on real-world data with complex mixtures of repetitive patterns, LSTNet achieved significant performance improvements over that of several state-of-the-art baseline methods. All the data and experiment codes are available online.

【现实意义】

多变量时间序列预测是跨多个领域的重要机器学习问题，包括太阳能发电厂能量输出、电力消耗和交通拥堵情况的预测。

【存在问题】

在这些实际应用中出现的时间数据通常涉及长期和短期模式的混合，对于这些模式，自回归模型和高斯过程等传统方法可能会失败。

【解决方案】

在本文中，我们提出了一种新颖的深度学习框架，即长期和短期时间序列网络 (Long- and Short-term Time-series network, LSTNet)，以应对这一开放挑战。 LSTNet 使用卷积神经网络 (CNN) 和循环神经网络 (RNN) 来提取变量之间的短期局部依赖模式，并发现时间序列趋势的长期模式。此外，我们利用传统的自回归模型来解决神经网络模型的尺度不敏感问题。

【实验结果】

在我们对具有重复模式的复杂混合的现实世界数据的评估中，LSTNet 比几种最先进的基线方法实现了显着的性能改进。所有数据和实验代码均可在线获取。

1 INTRODUCTION

【现实意义】

多元时间序列数据在我们的日常生活中无处不在，从股票市场的价格、高速公路上的交通流量、太阳能发电厂的输出、不同城市的温度等等，不一而足。在此类应用中，用户通常对基于对时间序列信号的历史观察预测新趋势或潜在危险事件感兴趣。例如，可以根据提前几个小时预测的交通拥堵模式制定更好的路线计划，通过对近期股市的预测获得更大的利润。

【存在问题】

多元时间序列预测经常面临一个重大的研究挑战，即如何捕捉和利用多个变量之间的动态依赖关系。具体来说，现实世界的应用程序通常需要混合使用短期和长期重复模式。

【举例说明】

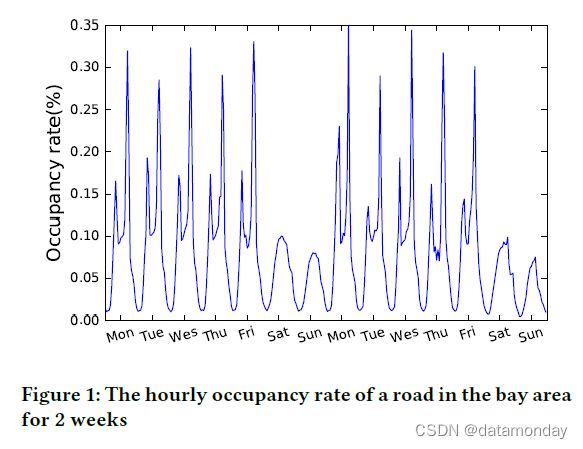
• 如图 1 所示，该图绘制了高速公路的每小时占用率。显然，有两种重复模式，每天和每周。前者描绘了早高峰与晚高峰，而后者则反映了工作日和周末的模式。一个成功的时间序列预测模型应该捕获这两种重复模式以进行准确的预测。
• 另一个例子，基于不同位置的大型传感器测量的太阳辐射来预测太阳能发电厂的输出的任务。长期模式反映白天与黑夜、夏季与冬季等之间的差异，短期模式反映云运动、风向变化等的影响。同样，没有考虑这两种循环模式，准确的时间序列预测是不可能的。

【已有研究的局限性】

然而，传统方法，如自回归方法 [2, 12, 22, 32, 35] 中的大量工作在这方面存在不足，因为它们中的大多数没有区分这两种模式，也没有明确和动态地模拟它们的交互。解决现有方法在时间序列预测中的这些局限性是本文的主要重点，为此我们提出了一个新的框架，该框架利用了深度学习研究的最新发展。

【从粗粒度上阐述与本文相关的工作，本文是RNN和CNN】

深度神经网络已在相关领域得到深入研究，并对广泛问题的解决产生了非凡的影响。例如，递归神经网络 (RNN) 模型 [9] 在最近的自然语言处理 (NLP) 研究中变得最流行。特别是 RNN 的两个变体，即长短期记忆 (LSTM) [15] 和门控循环单元 (GRU) [6]，显着提高了机器翻译、语音识别和其他 NLP 任务，因为它们可以根据输入文档中单词之间的长期和短期依赖关系有效地捕捉单词的含义 [1, 14, 19]。在计算机视觉领域，再举一个例子，卷积神经网络(CNN) 模型 [19, 21] 通过从输入图像中成功提取各种粒度级别的局部和移位不变特征（有时称为“shapelets”），显示出出色的性能。

【进一步阐述RNN和CNN应用于时间序列领域（分类，回归）的研究】

深度神经网络在时间序列分析中也受到越来越多的关注。先前工作的很大一部分都集中在时间序列分类上，即自动将类标签分配给时间序列输入的任务。例如，RNN 架构已被研究用于从医疗保健序列数据中提取信息模式 [5, 23]，并根据诊断类别对数据进行分类。 RNN 也被应用于移动数据，用于根据动作或活动对输入序列进行分类 [13]。 CNN 模型也被用于动作/活动识别 [13, 20, 31]，用于从输入序列中提取移位不变的局部模式作为分类模型的特征。

深度神经网络也被研究用于时间序列预测 [8, 33]，即使用过去观察到的时间序列来预测前瞻视野中的未知时间序列的任务——视野越大，越难预测。在这个方向上的努力范围从早期使用朴素 RNN 模型 [7] 和结合使用 ARIMA [3] 和多层感知器 (MLP) 的混合模型 [16, 34, 35] 到最近将 vanilla RNN 和时间序列预测中的动态玻尔兹曼机[8]。

【最后引出本文的解决方案及实验结果】

在本文中，我们提出了一个为多元时间序列预测设计的深度学习框架，即长期和短期时间序列网络 (LSTNet)，如图 2 所示。

• 利用两个卷积层的优势来发现局部多维输入变量和循环层之间的依赖模式，以捕获复杂的长期依赖关系。
• 一种新颖的循环结构 Recurrent-skip，旨在捕获非常长期的依赖模式，并使优化更容易，因为它利用了输入时间序列信号的周期性属性。
• 最后，LSTNet 将传统的自回归线性模型与非线性神经网络部分并行合并，使得非线性深度学习模型对于违反尺度变化的时间序列更加鲁棒。

在真实世界季节性时间序列数据集的实验中，我们的模型始终优于传统的线性模型和 GRU 递归神经网络。

【本文剩余部分内容的组织】

本文的其余部分安排如下。第 2 节概述了相关背景，包括具有代表性的自回归方法和高斯过程模型。第 3 节描述了我们提出的 LSTNet。第 4 节报告了我们模型的评估结果，并与真实数据集上的强基线进行了比较。最后，我们在第 5 节总结我们的发现。

2 RELATED BACKGROUND

【ARIMA模型家族的优缺点】

自回归综合移动平均 (autoregressive integrated moving average , ARIMA) 模型：最突出的单变量时间序列模型之一。

优点：其统计特性以及模型选择过程中著名的 Box-Jenkins 方法 [2]。 ARIMA 模型不仅适用于各种指数平滑技术 [25]，而且足够灵活，可以包含其他类型的时间序列模型，包括：

• 自回归 (autoregression, AR)
• 移动平均 (moving average, MA)
• 自回归移动平均 (Autoregressive Moving Average, ARMA)

缺点：ARIMA 模型，包括它们用于建模长期时间依赖关系的变体 [2]，由于其高计算成本而很少用于高维多元时间序列预测。

---

【VAR模型家族的优缺点】

向量自回归 (vector autoregression, VAR)：由于其简单性，是多元时间序列 [2, 12, 24] 中使用最广泛的模型。 VAR 模型自然地将 AR 模型扩展到多变量设置，它忽略了输出变量之间的依赖关系。

近年来，各种 VAR 模型取得了重大进展，包括：

• elliptical VAR model [27]：用于长尾时间序列
• structured VAR model [26]：用于更好地解释高维变量之间依赖关系

然而，VAR 的模型容量在时间窗口大小上呈线性增长，在变量数量上呈二次方增长。这意味着，在处理长期时间模式时，继承的大模型容易过拟合。为了缓解这个问题，[32] 提出将原始高维信号减少为低维隐藏表示，然后应用 VAR 进行预测，并选择多种正则化。

---

【线性回归+正则化的模型的优缺点】

时间序列预测问题也可以被视为具有时变参数的标准回归问题。因此，可以很自然地将具有不同损失函数和正则化项的各种回归模型应用于时间序列预测任务。例如：

• 线性支持向量回归 (SVR) [4, 17] 基于回归损失学习最大边距超平面，其中超参数 ϵ 控制预测误差的阈值。
• 岭回归（Ridge regression）可以通过将 ϵ 设置为零来从 SVR 模型中恢复。
• [22] 应用 LASSO 模型来鼓励模型参数的稀疏性，以便可以显示不同输入信号之间的有趣模式。

由于机器学习社区中有高质量的现成求解器，这些线性方法实际上对于多变量时间序列预测更有效。尽管如此，与 VAR 一样，这些线性模型可能无法捕捉多元信号的复杂非线性关系，从而以牺牲效率为代价导致性能下降。

---

【高斯过程的优缺点】

高斯过程 (GP) 是一种用于对函数连续域上的分布进行建模的非参数方法。这与由诸如 VAR 和 SVR 等参数化函数类定义的模型形成对比。

• [28] 中GP 可以应用于多元时间序列预测任务，并且可以用作贝叶斯推理中函数空间的先验。
• [10] 提出了一种具有 GP 先验的完全贝叶斯方法，用于非线性状态空间模型，能够捕捉复杂的动态现象。

然而，高斯过程的性能以高计算复杂度为代价。由于核矩阵的矩阵求逆，多变量时间序列预测的高斯过程的直接实现在观测数上具有三次复杂度。

3 FRAMEWORK

在本节中，我们首先制定时间序列预测问题，然后在下一部分讨论所提出的 LSTNet 架构（图 2）的细节。最后，我们介绍了目标函数和优化策略。

3.1 Problem Formulation

在本文中，我们对多元时间序列预测的任务感兴趣。更正式地说，给定一系列完全观察到的时间序列信号 $Y=y_1,y_2,...,y_T$ 其中 $y_t\in {\mathbb{R}}^n$，$n$ 是变量维度，我们旨在以滚动预测方式预测一系列未来信号。话虽如此，为了预测 $y_{T+h}$，其中 $h$ 是当前时间戳之前的理想范围，我们假设 $\{y_1,y_2,...,y_T\}$ 可用。同样，为了预测下一个时间戳 $y_{T+h+1}$ 的值，我们假设 $\{y_1,y_2,...,y_T,y_{T+1}\}$ 可用。因此，我们将时间戳 $T$ 处的输入矩阵表示为 $X_T=\{y_1,y_2,...,y_T\}\in {\mathbb{R}}^{n\times T}$。

在大多数情况下，预测任务的范围是根据环境设置的要求来选择的，例如对于流量使用，感兴趣的范围从几小时到一天不等；对于股市数据，即使是提前几秒/分钟的预测对于产生回报也很有意义。

图 2 概述了建议的 LSTnet 架构。 LSTNet 是一个深度学习框架，专为混合长期和短期模式的多变量时间序列预测任务而设计。在接下来的部分中，我们将详细介绍 LSTNet 的构建块。

3.2 Convolutional Component

LSTNet 第一层是一个没有池化的卷积网络，旨在提取时间维度上的短期模式以及变量之间的局部依赖关系。卷积层由多个宽度为 ω 和高度为 n 的滤波器组成（高度设置为与变量个数相同）。第 k 个滤波器扫描输入矩阵 X 并产生

其中 * 表示卷积运算，输出 hk 将是一个向量，RELU 函数为 RELU (x) = max(0, x)。我们通过在输入矩阵 X 的左侧进行零填充来使每个向量 hk 的长度为 T 。卷积层的输出矩阵大小为 dc × T，其中 dc 表示滤波器的数量。

3.3 Recurrent Component

卷积层的输出同时被馈送到 Recurrent 组件和 Recurrent-skip 组件（将在 3.4 小节中描述）。循环组件是一个带有门控循环单元 (GRU) [6] 的循环层，并使用 RELU 函数作为隐藏更新激活函数。在时间 t 的循环单元的隐藏状态计算为：

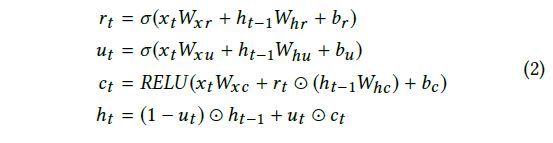
其中 ⊙ 是元素乘积（element-wise product），σ 是 sigmoid 函数，xt 是该层在时间 t 的输入。该层的输出是每个时间戳的隐藏状态。虽然研究人员习惯于使用 tanh 函数作为隐藏更新激活函数，但我们凭经验发现 RELU 导致更可靠的性能，通过它梯度更容易反向传播。

3.4 Recurrent-skip Component

带有 GRU [6] 和 LSTM [15] 单元的循环层经过精心设计，可以记住历史信息，从而了解相对长期的依赖关系。然而，由于梯度消失，GRU 和 LSTM 在实践中通常无法捕捉到非常长期的相关性。我们建议通过一种新颖的循环跳过组件来缓解这个问题，该组件利用现实世界集中的周期性模式。例如，每天的用电量和交通使用量都呈现出明显的规律。如果我们想预测今天 2 点的用电量，季节性预测模型中的一个经典技巧是利用历史日期中的 2 点记录，以及最近的记录。由于一个周期（24 小时）的长度极长以及随后的优化问题，这种类型的依赖关系很难被现成的循环单元捕获。受此技巧有效性的启发，我们开发了一种具有时间跳跃连接的循环结构，以扩展信息流的时间跨度，从而简化优化过程。具体来说，在当前隐藏单元和相邻周期中相同阶段的隐藏单元之间添加跳跃链接。更新过程可以表述为：

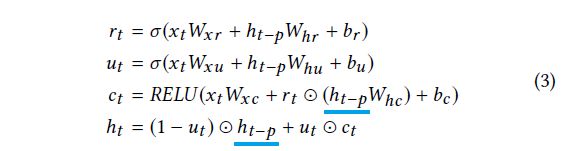
其中该层的输入是卷积层的输出，p 是跳过的隐藏单元的数量。对于具有明确周期性模式的数据集（例如，对于每小时用电量和交通使用数据集，p = 24），p 的值可以很容易地确定，并且必须进行调整。在我们的实验中，我们凭经验发现，即使在后一种情况下，经过良好调整的 p 也可以显着提高模型性能。此外，LSTNet 可以很容易地扩展为包含跳跃长度 p 的变体。

我们使用全连接层来组合 Recurrent 和 Recurrent-skip 组件的输出。全连接层的输入包括：

• Recurrent 组件在时间戳 t 的隐藏状态，用 $h_t^R$ 表示，

• 从时间戳 $t-p+1$ 到 $t$ 的 Recurrent-skip 组件的 p 个隐藏状态，用 $h_{t-p+1}^S,h_{t-p+2}^S,...,h_t^S$ 表示 。

全连接层的输出计算为：

其中 $h_t^D$ 是图 2 中神经网络（上）部分在时间戳 $t$ 处的预测结果。

3.5 Temporal Attention Layer

然而，Recurrent-skip 层需要一个预定义的超参数 p，这在非季节性时间序列预测中是不利的，或者其周期长度随时间变化。为了缓解这个问题，我们考虑了另一种方法，注意力机制[1]，它在输入矩阵的每个窗口位置学习隐藏表示的加权组合。具体来说，当前时间戳 t 处的注意力权重 ${\alpha }_t\in {\mathbb{R}}^q$ 计算为

$${\alpha }_t=AttnScore(H_t^R,h_{t-1}^R)$$

其中 $H_t^R=[h_{t-q}^R,...,h_{t-1}^R]$ 是按列堆叠 RNN 的隐藏表示的矩阵，AttnScore 是一些相似函数，例如点积、余弦或由简单的多层感知器参数化。

时间注意层的最终输出是加权上下文向量 $c_t=H_t{\alpha }_t$ 和最后一个窗口隐藏表示 $h_{t-1}^R$ 的连接，以及线性投影操作

$$h_t^D=W[c_t;h_{t-1}^R]+b.$$

3.6 Autoregressive Component

由于卷积和循环组件的非线性特性，神经网络模型的一个主要缺点是输出的规模对输入的规模不敏感。不幸的是，在特定的真实数据集中，输入信号的规模以非周期性的方式不断变化，这大大降低了神经网络模型的预测精度。 4.6 节给出了这种失败的具体例子。为了解决这个缺陷，在类似于 highway network [29]，我们将 LSTNet 的最终预测分解为线性部分，主要关注局部缩放问题，加上包含重复模式的非线性部分。在 LSTNet 架构中，我们采用经典的自回归 (AR) 模型作为线性组件。将 AR 分量的预测结果记为 $h_t^L\in {\mathbb{R}}^n$，将 AR 模型的系数记为 $W^{ar}\in {\mathbb{R}}^{q^{ar}}$ 和 $b^{ar}\in \mathbb{R}$，其中 $q^{ar}$ 是输入矩阵上输入窗口的大小。请注意，在我们的模型中，所有维度共享同一组线性参数。 AR 模型公式如下，

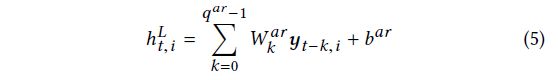
然后通过整合神经网络部分和 AR 组件的输出来获得 LSTNet 的最终预测：

其中 ${\hat{Y}}_t$ 表示模型在时间戳 $t$ 处的最终预测。

3.7 Objective function

平方误差是许多预测任务的默认损失函数，相应的优化目标表示为，

其中 Θ 表示模型的参数集，ΩTrain 是用于训练的时间戳集，|| · ||F 是 Frobenius 范数，h 是 3.1 节中提到的范围。传统的带有平方损失函数的线性回归模型被命名为 Linear Ridge，相当于带有岭正则化的向量自回归模型。然而，实验表明，线性支持向量回归（线性 SVR）[30] 在某些数据集中优于线性岭模型。线性 SVR 和线性岭之间的唯一区别是目标函数。线性 SVR 的目标函数是，

其中 C 和 ϵ 是超参数。受线性 SVR 模型卓越性能的启发，我们将其目标函数纳入 LSTNet 模型作为平方损失的替代方案。为简单起见，我们假设 ϵ = 0¹，上面的目标函数简化为绝对损失（L1-loss）函数如下：

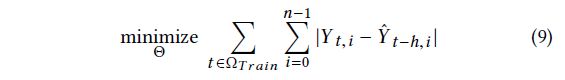
绝对损失函数的优点是它对实时序列数据中的异常具有更强的鲁棒性。在实验部分，我们使用验证集来决定使用哪个目标函数，平方损失 Eq.7 或绝对损失 Eq.9。

3.8 Optimization Strategy

在本文中，我们的优化策略与传统时间序列预测模型中的优化策略相同。假设输入时间序列为 Yt = {y1,y2, . . . ,yt }，我们定义了一个可调窗口大小 q，并将时间戳 t 处的输入重新表述为 Xt = {yt−q+1,yt−q+2, . . . ,yt }。然后，该问题成为具有一组特征值对 {Xt ,Yt+h } 的回归任务，并且可以通过随机梯度体下降 (SGD) 或其变体（例如 Adam [18]）来解决。

4 EVALUATION

我们在 4 个基准数据集上使用 9 种方法（包括我们的新方法）进行了广泛的实验，用于时间序列预测任务。所有数据和实验代码均可在线获取。

4.1 Methods for Comparison

我们比较评估的方法如下。

• AR 代表自回归模型，相当于一维VAR模型。
• LRidge 是具有L2 正则化的向量自回归 (VAR) 模型，它在多元时间序列预测中最为流行。
• LSVR 是具有支持向量回归目标函数的向量自回归 (VAR) 模型 [30]。
• TRMF 是使用[32] 的时间正则化矩阵分解的自回归模型。
• GP 是用于时间序列建模的高斯过程。 [11, 28]
• VAR-MLP 是[35] 中提出的模型，它结合了多层感知（MLP）和自回归模型。
• RNN-GRU 是使用 GRU 单元的循环神经网络模型。
• LSTNet-skip 是我们提出的带有skip-RNN 层的LSTNet 模型。
• LSTNet-Attn 是我们提出的具有时间注意层的 LSTNet 模型。

对于上面的 AR、LRidge、LSVR 和 GP 等单输出方法，我们只是独立训练了 n 个模型，即 n 个输出变量中的每一个都训练一个模型。

4.2 Metrics

我们使用了三个传统的评估指标，定义为：

其中 $Y,\hat{Y}\in {\mathbb{R}}^{n\times T}$ 分别是真实信号和系统预测信号。RSE 是广泛使用的均方根误差 (RMSE) 的缩放版本，旨在使评估更具可读性，无论数据规模如何。 RSE 值越低越好，而 CORR 值越高越好。

4.3 Data

我们使用了四个公开可用的基准数据集。表 1 总结了语料库的统计数据。

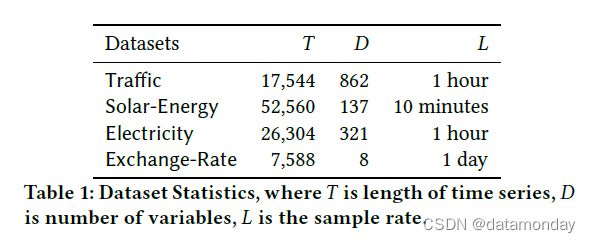
Traffic：加州交通部 48 个月（2015-2016）每小时数据的集合。该数据描述了旧金山湾区高速公路上不同传感器测量的道路占用率（介于 0 和 1 之间）。

Solar-Energy：2006 年的太阳能发电记录，每10 分钟从阿拉巴马州的137 个光伏电站采样一次。

Electricity：从2012 年到2014 年，每15 分钟记录一次电力消耗，单位为千瓦时，n = 321 个客户。我们转换数据以反映每小时消耗量；

Exchange-Rate：澳大利亚、英国、加拿大、瑞士、中国、日本、新西兰、新加坡等8个国家在1990年至2016年的每日汇率汇总。

所有数据集按时间顺序分为训练集（60%）、验证集（20%）和测试集（20%）。为了促进多元时间序列预测的未来研究，我们在网站上公开了所有原始数据集和预处理后的数据集。

为了检查时间序列数据中长期和/或短期重复模式的存在，在图 3 中，从四个数据集中随机选择一些变量绘制了自相关图。自相关，也称为序列相关，是一个信号，其自身的延迟副本是下面定义的延迟函数

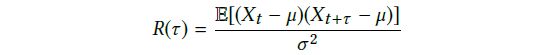
其中 Xt 是时间序列信号，μ 是均值，σ2 是方差。在实践中，我们考虑经验无偏估计量来计算自相关。

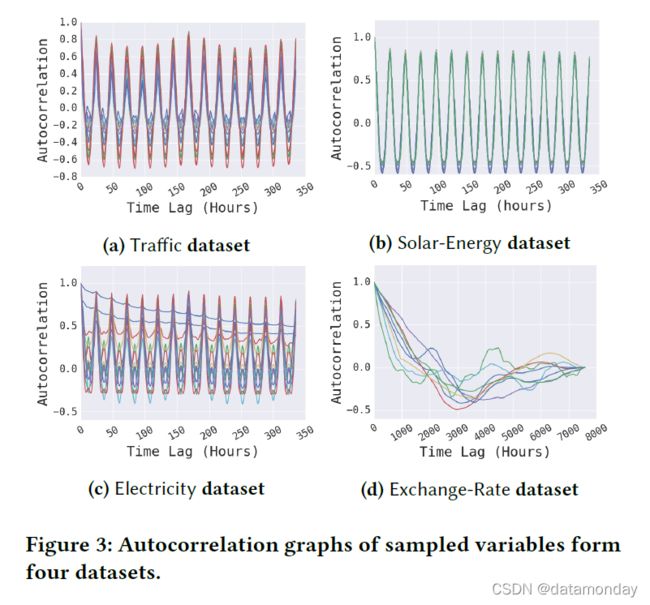
我们可以在图 3 的图表 (a)、(b) 、© 和 (d) 中看到：

• 在交通、太阳能和电力数据集中存在具有高自相关性的重复模式，但在汇率数据集中没有。
• 在 Traffic 和 Electricity 数据集的图中，观察到短期每日模式（每 24 小时）和长期每周模式（每 7 天），这完美反映了高速公路交通情况的预期规律性和电力消耗。
• 在汇率数据集的图 (d) 中，几乎看不到任何重复的长期模式，预计会有一些短期的局部连续性。

这些观察对于我们以后分析不同方法的实证结果很重要。也就是说，对于能够正确建模并成功利用数据中短期和长期重复模式的方法，当数据包含此类重复模式（如电力、交通和太阳能）时，它们应该表现出色。另一方面，如果数据集不包含此类模式（如汇率），则这些方法的优势可能不会比其他功能较弱的方法带来更好的性能。我们将在第 4.7 节中用经验论证重新讨论这一点。

4.4 Experimental Details

我们对每个方法和数据集的保留验证集上的所有可调超参数进行网格搜索。具体来说，所有方法共享相同的窗口大小 q 的网格搜索范围，范围从 {20, 21, . . . , 29} 如果适用。对于 LRidge 和 LSVR，正则化系数 λ 选自 {2−10, 2−8, . . . , 28, 210}。对于 GP，RBF 内核带宽 σ 和噪声水平 α 选自 {2−10, 2−8, . . . , 28, 210}。对于 TRMF，隐藏维度选自 {22, . . . , 26} 和正则化系数 λ 从 {0.1, 1, 10} 中选择。对于 LST-Skip 和 LST-Attn，我们采用了第 3.8 节中描述的训练策略。循环和卷积层的隐藏维度从 {50, 100, 200} 和 {20, 50, 100} 中选择用于循环跳过层。对于交通和电力数据集，循环跳跃层的跳跃长度 p 设置为 24，对于太阳能和汇率数据集，调整范围从 21 到 26。 AR 分量的正则化系数从 {0.1, 1, 10} 中选择以达到最佳性能。我们在每一层之后执行 dropout，除了输入和输出层，并且速率通常设置为 0.1 或 0.2。 Adam[18] 算法用于优化模型的参数。

4.5 Main Results

表 2 总结了所有方法（8）在所有指标（3）中对所有测试集（4）的评估结果。我们分别设置horizon = {3, 6, 12, 24}，这意味着对于电力和交通数据的预测，范围设置为3到24小时，对于太阳能数据的预测设置为30到240分钟，对于汇率数据从 3 到 24 天。视野越大，预测任务就越难。每个（数据、指标）对的最佳结果在此表中以粗体突出显示。 LSTNet-Skip（提出的 LSTNet 的一个版本）的粗体结果总数为 17，LSTNet-Attn（我们的 LSTNet 的另一个版本）为 7，其余方法的总数为 0 到 3。

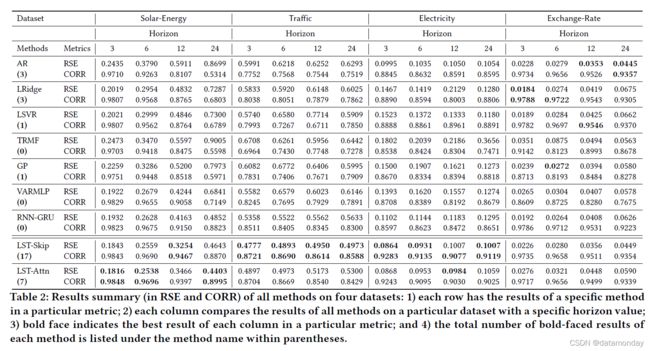
• 显然，LSTNet-skip 和 LSTNet-Attn 这两个提出的模型在具有周期性模式的数据集上持续增强了现有技术，尤其是在大视野的设置中。
• 此外，当预测范围为 24 时，LSTNet 在太阳能、交通和电力数据集的 RSE 指标上分别优于基线 RNN-GRU 9.2%、11.7%、22.2%，证明了框架设计对复杂重复模式的有效性。
• 更重要的是，当周期性模式 q 从应用程序中不清楚时，用户可以考虑 LSTNet-attn 作为 LSTNet-skip 的替代方案，因为前者仍然比基线产生了相当大的改进。但提议的 LSTNet 在 Exchange-Rate 数据集上比 AR 和 LRidge 稍差。为什么？回想一下，在第 4.3 节和图 3 中，我们使用这些数据集的自相关曲线来显示 SolarEnergy、Traffic 和 Electricity 数据集中存在重复模式，但 Exchange-Rate 中没有。
• 当前的结果为 LSTNet 模型在数据中确实出现长期和短期依赖模式时成功建模提供了经验证据。否则，LSTNet 的表现与代表性基线中较好的（AR 和 LRidge）相当。

将单变量 AR 的结果与多变量基线方法（LRidge、LSVR 和 RNN）的结果进行比较，我们看到在某些数据集中，即 Solar-Energy 和 Traffic，多变量方法更强，但在其他方面更弱，这意味着更丰富输入信息会导致传统多变量方法的过度拟合。相比之下，LSTNet 在不同情况下具有强大的性能，部分原因在于它的自回归组件，我们将在 4.6 节进一步讨论。

4.6 Ablation Study

为了证明我们的框架设计的效率，我们进行了仔细的消融研究。具体来说，我们在 LSTNet 框架中一次删除每个组件。首先，我们将没有不同组件的 LSTNet 命名如下。

• LSTw/oskip：没有 Recurrent-skip 组件和注意力组件的 LSTNet 模型。
• LSTw/oCNN：没有卷积组件的 LSTNet-skip 模型。
• LSTw/oAR：没有AR 组件的 LSTNet-skip 模型。

对于不同的基线，我们调整模型的隐藏维度，使它们具有与完整的 LSTNet 模型相似数量的模型参数，消除了由模型复杂性引起的性能增益。

使用 RSE 和 CORR 测量的测试结果如图 5 6 所示。这些结果的几个观察结果值得强调：

• 每个数据集的最佳结果是使用 LSTSkip 或 LST-Attn 获得的。
• 从完整模型中删除 AR 组件（在 LSTw/oAR 中）导致大多数数据集的性能下降最为显着，总体上显示了 AR 组件的关键作用。
• 删除（LSTw/oCNN 或 LSTw/oskip）中的 Skip 和 CNN 组件会导致某些数据集的性能大幅下降，但并非全部。LSTNet 的所有组件共同导致我们的方法在所有数据集上的稳健性能。

结论是，我们的架构设计在所有实验设置中都是最稳健的，尤其是在大的预测范围时。至于为什么 AR 组件会发挥如此重要的作用，我们的解释是 AR 通常对数据的规模变化具有鲁棒性。

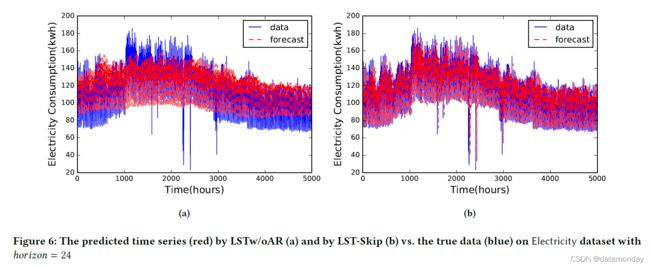
为了从经验上验证这种直觉，我们在图 6 中绘制了电力消耗数据集中 1 到 5000 小时持续时间的一维（一个变量）时间序列信号，其中蓝色曲线是真实数据，红色曲线是系统- 预测信号。我们可以看到，真正的消耗在第 1000 小时左右突然增加，LSTNet-Skip 成功捕捉到了这种突然的变化，但 LSTw/oAR 未能正确反应。

为了更好地验证这个假设，我们进行了模拟实验。首先，我们通过以下步骤随机生成一个尺度变化的自回归过程。首先，我们随机采样一个向量 w ∼ N (0, I),w ∈ Rp，其中 p 是给定的窗口大小。那么生成的自回归过程 xt 可以描述为

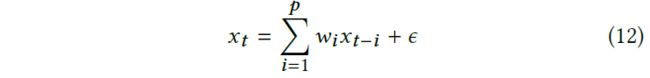
其中 ϵ ∼ N (µ, 1)。为了注入尺度变化，我们将高斯噪声的平均值每 T 个时间戳增加 µ0。则时间序列 xt 的高斯噪声可写为

其中⌊·⌋表示底函数。

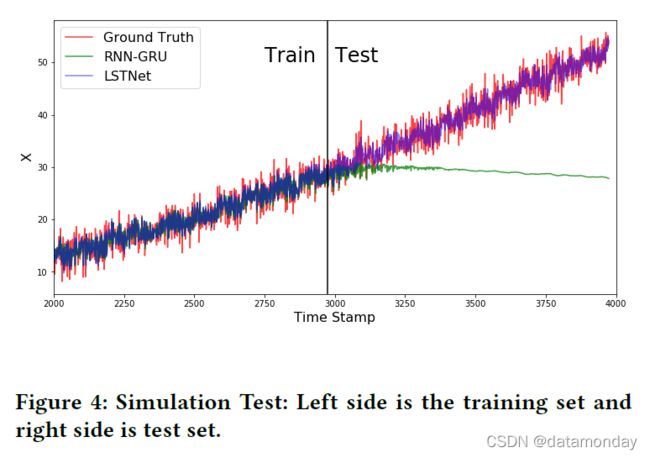
我们将时间序列拆分为训练集并按时间顺序进行测试，并测试 RNN-GRU 和 LSTNet 模型。结果如图 4 所示。RNN-GRU 和 LSTNet 都可以记住训练集中的模式（左侧）。但是，RNN-GRU 模型无法遵循测试集中的尺度变化模式（右侧）。相反，LSTNet 模型更适合测试集。换句话说，普通的 RNN 模块，或者说 LSTNet 中的神经网络组件，可能对数据中违反的尺度波动不够敏感（这在电力数据中很典型，可能是由于公共假期的随机事件或温度波动等），而简单的线性AR模型可以在预测中做出适当的调整。

总之，这项消融研究清楚地证明了我们架构设计的效率。所有组件都为 LSTNet 的出色而强大的性能做出了贡献。

4.7 Mixture of long- and short-term patterns

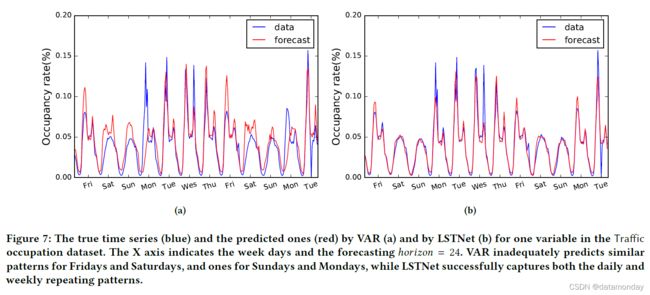
为了说明 LSTNet 在对时间序列数据中短期和长期重复模式混合建模方面的成功，图 7 比较了数据集 LSTNet 和 VAR 在 Traffic 中特定时间序列（输出变量之一）上的性能。如第 4.3 节所述，流量数据表现出两种重复模式，即每日和每周。我们可以在图 7 中看到，

• 周五和周六的真实交通占用模式（蓝色）非常不同，而周日和周一则不同。
• 图 7 是交通流量监控传感器的 VAR 模型（（a）部分）和 LSTNet（（b）部分）的预测结果，其中它们的超参数是根据验证集上的 RMSE 结果选择的。该图表明，VAR 模型只能处理短期模式。 VAR 模型的预测结果模式只取决于预测的前一天。我们可以清楚地看到它在星期六（第 2 和第 9 个峰值）和星期一（第 4 和第 11 个峰值）的结果与 ground truth 不同，其中星期一（工作日）的 ground truth 有两个峰值，一个峰值为星期六（周末）。
• 相反，我们提出的 LSTNet 模型分别在工作日和周末执行两种模式。这个例子证明了 LSTNet 模型能够同时记忆短期和长期重复模式的能力，这是传统预测模型所不具备的，在现实世界时间序列信号的预测任务中至关重要。

5 CONCLUSION

在本文中，我们提出了一种用于多变量时间序列预测任务的新型深度学习框架 (LSTNet)。通过结合卷积和递归神经网络的优势以及自回归组件，所提出的方法显着改善了在多个基准数据集上进行时间序列预测的最新结果。通过深入的分析和经验证据，我们展示了 LSTNet 模型架构的效率，它确实成功地捕获了数据中的短期和长期重复模式，并结合了线性和非线性模型来进行稳健的预测。

对于未来的研究，扩展工作有几个有希望的方向。首先，跳跃循环层的跳跃长度 p 是一个关键的超参数。目前，我们根据验证数据集手动调整它。如何根据数据自动选择p是一个有趣的问题。其次，在卷积层中我们平等对待每个可变维度，但在现实世界的数据集中，我们通常拥有丰富的属性信息。将它们集成到 LSTNet 模型中是另一个具有挑战性的问题。