Muasci

BILSTM+CRF用于NER原理与代码详解(+并行化的理解)

文章目录

前言:命名实体识别
原理+代码介绍:
- 原理之BILSTM:
- 原理之CRF(*):
- - 损失函数之正确路径的分数:
  - 损失函数之所有路径的分数:
  - 损失函数之最大化正确路径的概率
  - 损失函数之logsumexp思路(*)
- CRF代码优化(并行化计算)
- - 并行化计算之单个句子
  - 并行化计算之batch
后记
参考

前言:命名实体识别

命名实体识别的任务就是识别出待处理文本中三大类（实体类、时间类和数字类）、七小类（人名、机构名、地名、时间、日期、货币和百分比）命名实体。
本次实验中，使用Conll2003dataset数据集，其中含有三个文件:

数据集共包含:B-MISC\B-ORG\B-LOC\I-MISC\I-ORG\I-LOC\I-PER\O，这8类实体类型。

原理+代码介绍:

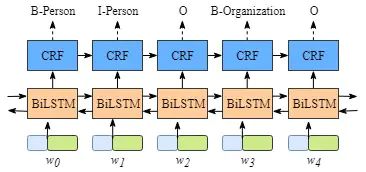
接下来将介绍BILSTM+CRF用于NER,模型用李宏毅老师课中一张生动图表示为:

下层是RNN、LSTM等序列模型，输入单词序列，输出推测的实体类别概率；将实体类别概率进一步输入HMM、CRF等模型，进一步捕捉标签之间的前后关系。

原理之BILSTM:

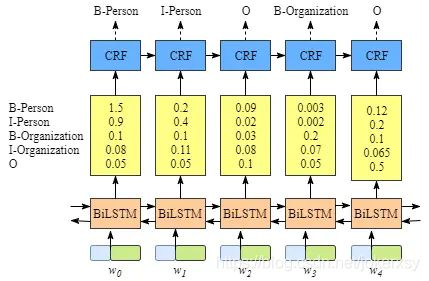
BILSTM不多介绍，总体的模型如下:

其中，BILSTM层的具体输出如下:

对于一个输入序列而言，每一个单词经过词嵌入或者随机初始化(1)，输入到BILSTM中，BILSTM输出每一个词向量的隐藏层向量(2)，隐藏层向量会接着进入线性层，输出固定维度(=标签数量)的向量，该向量表示不同标签的预测概率(3)。

对应的代码为:

   def _get_lstm_features(self, sentence):
       self.hidden = self.init_hidden()  # 随机初始化隐藏层权重
       embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)  # (1)embdding
       lstm_out, self.hidden = self.lstm(embeds, self.hidden)  # (2)得到所有单词的隐藏层
       lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
       lstm_feats = self.hidden2tag(lstm_out)  # (3)进入线性层，得到预测概率
       return lstm_feats

考虑单个句子，单词数为N，经过embedding变为N x word_dim，经过bilstm变为N x hidden_dim，经过线性层变为N x tag_num。

原理之CRF(*):

理解CRF的损失函数是理解整个模型的关键！
我们已经从BILSTM那儿得到了N x tag_num大小的矩阵P(称之为发射矩阵)，其中 $P_{ij}$ 表示:第i个单词发射(预测)到第j个实体标签的概率。

除了发射矩阵外，CRF模型还自带一个转移矩阵A(tag_num x tag_num)，其中 $A_{ij}$ 表示:第j个标签转移到第i个标签的概率(注意:代码里就是这样的，而不是第i个标签转移到第j个标签的概率)。

经过推导就可以发现，损失函数主要由两部分组成:

正确路径的分数
所有路径的分数之和

不要急，我们接下来利用发射矩阵和转移矩阵来解释什么是"正确路径的分数"、“所有路径的分数之和”，然后进一步定义"CRF的损失函数"

损失函数之正确路径的分数:

我们的训练集是有标签的数据，对于词序列(观测序列){ $w_i$ ,i=1,2…n}，对应有一个正确的标签序列{ $y_i$ ,i=1,2…n}。
这里借用一下上文的发射矩阵和转移矩阵中元素的概念，定义这个正确路径的分数公式:

理解为:标签序列转移分数之和 + 观测序列与标签序列之间的发射概率之和。更详细一点说，我们明确一串词序列{ $w_i$ ,i=1,2…n}和对应的一串标签序列{ $y_i$ ,i=1,2…n}，那么我们就可以计算:【单词 $w_1$ 发射(预测)到标签 $y_1$ 的概率+标签 $y_0$ 转移到标签 $y_1$ 的概率】 + 【单词 $w_2$ 发射(预测)到标签 $y_2$ 的概率+标签 $y_1$ 转移到标签 $y_2$ 的概率】+ …，也就是上面式子的表示。
注意到我们一开始有一个叫做"标签 $y_0$ 转移到标签 $y_1$ 的概率"，这里的标签 $y_0$ 我们在代码里讲其定义为start，对应的，我们有一个标签 $y_{n+1}$ ，它表示end。

损失函数之所有路径的分数:

以上是正确路径的分数。正如之前所说，bilstm的输出结果表明，我们在做预测时，N个单词，会得到N x tag_num的发射(预测)矩阵，也就是说，每一个单词都会得到一个tag_num维的向量，表示对所有标签发射的概率。
所以我们就知道，对于一个观测序列，我们总共能够得到： $tag\_num^{N}$ 条路径，每一条路径都可以用上面的方式计算得到一个分数。进一步我们利用softmax函数，为上面讲的正确路径的分数定义一个概率值( $Y_X$ 表示所有的tag序列(路径))

这个概率值已经有损失函数那味儿了，因为直观地，它越大，我们的预测就越准确。

损失函数之最大化正确路径的概率

因此，我们训练的目的其实就是:最大化似然概率 $P (y ∣ X)$ ，(采用对数似然能够方便计算):

损失函数是要最小化的，我们将损失函数定义为: $- l o g (p (y ∣ X))$ 。
我们就得到了损失函数，就要计算之，利用上面的方法我们也是可以算的。但是复杂度有点高(下面会说)，所以下面的内容，都是在介绍一种简便的计算方式，这也是pytorch官网那份代码背后的思想。

正文:
正确路径的分数: $S (X, y)$ 是很好求的，只要得到两个矩阵，取出对应元素相加就可以了
剩下就是求解下式了:

按理说我们可以跟正确路径一样，去求解所有路径的分数，然后去exp，然后相加，然后取log，就能够得到答案，但如上所述我们一共有 $tag\_num^{N}$ 条路径，一一求解复杂度实在太高，下面引出理解损失函数代码的关键——logsumexp思路,下面是我看到的思路出处:
Bi-LSTM-CRF for Sequence Labeling

损失函数之logsumexp思路(*)

大佬的原话是

一种简便的方法，对于到词 $w_{i+1}$ 的路径，可以先把到词 $w_{i}$ 的logsumexp计算出来，因为下图公式，因此先计算每一步的路径分数和直接计算全局分数相同，但这样可以大大减少计算的时间。

隔了好久，又回过头来看了一遍，感觉上面的公式可以用下面的式子来解释(你可以先跳过这里，看到下面再来看这个)

$log^{e^{score(N,N)}+e^{score(V,N)}} + score(N,N)$
$log^{e^{score(N,N)+score(N,N)}+e^{score(V,N)+score(N,N)}}$

如何理解这个公式?
对于这一公式Pytorch Bi-LSTM + CRF 代码详解——Johnny_Cuii
这篇博客做了很详细的介绍，但我认为该篇在exp部分并不正确，我将引用里面的例子，来正确地推导这一公式:

哦对了，推导之前，先把官网这一部分的代码放上，便于理解:

def _forward_alg(self, feats):
    # Do the forward algorithm to compute the partition function
    init_alphas = torch.Tensor(1, self.tagset_size).fill_(-10000.)
    # START_TAG has all of the score.
    init_alphas[0][self.tag_to_ix[START_TAG]] = 0.

    # Wrap in a variable so that we will get automatic backprop
    forward_var = autograd.Variable(init_alphas)

    # Iterate through the sentence
    for feat in feats:
        alphas_t = []  # The forward variables at this timestep
        for next_tag in range(self.tagset_size):
            # broadcast the emission score: it is the same regardless of
            # the previous tag
            emit_score = feat[next_tag].view(
                1, -1).expand(1, self.tagset_size)
            # the ith entry of trans_score is the score of transitioning to
            # next_tag from i
            trans_score = self.transitions[next_tag].view(1, -1)
            # The ith entry of next_tag_var is the value for the
            # edge (i -> next_tag) before we do log-sum-exp
            next_tag_var = forward_var + trans_score + emit_score
            # The forward variable for this tag is log-sum-exp of all the
            # scores.
            alphas_t.append(log_sum_exp(next_tag_var))
        forward_var = torch.cat(alphas_t).view(1, -1)
    terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
    alpha = log_sum_exp(terminal_var)
    return alpha

OK，我保证你会看懂上面那个公式的。
先做三个假设:

假设观测序列为句子【我爱中华人民】
假设词性一共只有两种: 名词N 和动词V
假设 ${score(N,N,N)}$ 表示:标注序列为N,N,N的路径分数(【我】、【爱】、【中华人民】都预测为了N(名词))

我们要对这个句子求

也就是对这个句子所有可能的标注序列，都算出来他们的Score。我们需要按照大佬的话来计算，就是“如果要求，到词’中华人民‘为止的路径，可以先把，到’爱‘位置，路径的logsumexp计算出来”。

【我爱】的词性组合一共有四种:

第一步:当【爱】标注为N
当【爱】标注为N时，【我】可能是N或V，可以这样理解：当前发射概率就一个值，那就是【爱】发射到N这个标签的概率；转移概率是一个有两个值的向量，两个值分别表示上一个的标签(【我】的标签)为N时，转移到N的概率；上一个的标签(【我】的标签)为V时，转移到N的概率。
所以官网代码有下面这一句:也就是把发射概率也扩充成一个有两个值的向量(next_tag)就是【爱】当前的发射标签:N)

emit_score = feat[next_tag].view(
                1, -1).expand(1, self.tagset_size)

而转移概率很容易得到，就是从转移矩阵A中索引得到，之前说过转移矩阵A中， $A_{ij}$ 表示标签j转移到标签i的概率，那么下面代码取出的向量就代表着所有可能的标签转移到next_tag这个标签的概率:

trans_score = self.transitions[next_tag].view(1, -1)

我们把这两个分数相加(暂时忽略forward_var，但后面它是logsumexp的核心)，其实就得到了一个两个值的向量
[ $s c o r e (N, N), s c o r e (V, N)$ ]：

next_tag_var = forward_var + trans_score + emit_score

然后对这个向量进行log_sum_exp(先exp，再sum，再log)，就能够得到 $log^{e^{score(N,N)}+e^{score(V,N)}}$ ，把这个值放进一个列表:

alphas_t.append(log_sum_exp(next_tag_var))

接着，代码进入了下一个循环:

第二步:当【爱】标注为V
当【爱】标注为V时，【我】同样可能是N或V，然后经过完全一样的操作（所以你看上面的代码其实是通过for next_tag in range(self.tagset_size)进入了一个完全一样的循环），我们得到了一个两个值的向量[ $s c o r e (N, V), s c o r e (V, V)$ ]

然后同样的，进行log_sum_exp，就能得到 $log^{e^{score(N,V)}+e^{score(V,V)}}$ ，仍旧把这个值放进一个列表

alphas_t.append(log_sum_exp(next_tag_var))

好了，经过两个循环，两个append，我们看一下alphas_t这个列表里的值:
$log^{e^{score(N,N)}+e^{score(V,N)}}$
$log^{e^{score(N,V)}+e^{score(V,V)}}$

第三步:考虑【中华人民】标注为N\V
第一第二步，我们已经把到【爱】这个词的路径的score都求了出来，已经初步完成了大佬所说的:

对于到词 $w_{i+1}$ 的路径，可以先把到词 $w_{i}$ 的logsumexp计算出来

只不过，暂时分成了上面列表中的两个值，存放在alphas这个列表中(这也是log_sum_exp的关键)，接下来我们考虑【中华人民】这个词:
当【中华人民】标注为N时，同样的，通过下面语句，得到【中华人民】到标签N的发射向量，向量中两个值是相等的

# 注意:现在代码已经通过for feat in feats:进入了考虑下一个词的循环了！
emit_score = feat[next_tag].view(
                1, -1).expand(1, self.tagset_size)

然后通过索引，得到所有可能的标签转移到N这个标签的概率

 trans_score = self.transitions[next_tag].view(1, -1)

接下来的这句代码，就是log_sum_exp的核心，也就是

next_tag_var = forward_var + trans_score + emit_score

请注意现在的forward_var，现在的forward_var，就是第二步中的alphas_t这个向量，因为在第二步结束，跳出循环后，会有下面的语句:

forward_var = torch.cat(alphas_t).view(1, -1)

一步一步来，我们先算【中华人名】为N标签这轮循环的trans_score+emit_score,我们得到一个两个值的向量:
$s c o r e (N, N)$
$s c o r e (V, N)$
那么当前的forward+tran_score+emit_score就可以理解为得到下面的向量:
$log^{e^{score(N,N)}+e^{score(V,N)}} + score(N,N)$
$log^{e^{score(N,V)}+e^{score(V,V)}} + score(V,N)$
也就是
$log^{e^{score(N,N)}+e^{score(V,N)}} + log^{e^{score(N,N)}}$
$log^{e^{score(N,V)}+e^{score(V,V)}} + log^{e^{score(V,N)}}$
也就是
$log^{e^{score(N,N)}*{e^{score(N,N)}}+e^{score(V,N)}*{e^{score(N,N)}}}$
$log^{e^{score(N,V)}*e^{score(V,V)}+e^{score(V,N)}*e^{score(V,N)}}$
也就是
$log^{e^{score(N,N)+score(N,N)}+e^{score(V,N)+score(N,N)}}$
$log^{e^{score(N,V)+score(V,V)}+e^{score(V,N)+score(V,N)}}$
你还记得score(？,？)的定义吗？它跟正确路径的分数一样，通过下式计算

全都是加法，那我们当然可以进行合并，得一个两个值的向量:
$log^{e^{score(N,N,N)}+e^{score(V,N,N)}}$
$log^{e^{score(N,V,N)}+e^{score(V,V,N)}}$
我们对这个向量做log_sum_exp,不难计算,就可以得到下值:

$log^{e^{score(N,N,N)}+e^{score(V,N,N)}+e^{score(N,V,N)}+e^{score(V,V,N)}}$

将这个值append到alphas中。

之后

接下来会考虑【中华人民】标注为V时的情况，也一样，然后也append到alphas_t中，就会是这样一个向量:

$log^{e^{score(N,N,N)}+e^{score(V,N,N)}+e^{score(N,V,N)}+e^{score(V,V,N)}}$
$log^{e^{score(N,N,V)}+e^{score(V,N,V)}+e^{score(N,V,V)}+e^{score(V,V,V)}}$

有没有发现，现在的alphas_t记录了【我爱中华人民】所有的 2^3 = 8 条路径，只不过分成了两个值，存储在alphas_t中

我们通过下面语句，即考虑转移到这个标签的概率,得到最终的向量

terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]

然后最后做一次:

 alpha = log_sum_exp(terminal_var)

就能够得到所谓的:

我后来想了一下，思路大体是对的，但代码并不完全是这样。一开始的forward_var就是一个向量[0,-1000,-1000,-1000]，你可能会好奇为什么有4个值，因为前两个分别代表start和end，由于再展开讲太复杂了，而且我也没有很好的理解，就不继续说了。另外，forward_var会通过cat不断增长，所以每遍历一个新的feat，forward_var就会增长target_num的长度。这里面的计算细节，感兴趣的可以自己去算算，我是算不动了，深感抱歉！

CRF代码优化(并行化计算)

其实，了解到上面，官网的代码就已经能看懂了(只需要再去了解一下维特比)，但这里将结合代码提出一种并行化计算的方法

并行化计算之单个句子

单个句子的原理分析，一定要先看长文详解基于并行计算的条件随机场CRF
这篇文章让我理解了并行计算的具体方案，说白了就是如何更高效地利用的forward_var(记录了之前的所有分数)，发射矩阵，转移矩阵来计算出我们要的分数:

forward_var在一个feat的循环中，会被重复用到tag_num次，这是因为：考虑当前这个单词的tag_num个可能的tag，每一个tag都会考虑前面那个单词的所有tag下的分数，而这个信息就是存储在了forward_var中最新cat到里面的那一行。所以我们只需要取出最底下那一行，然后可以用torch.stack来重复tag_num次，形成一个矩阵（记作H）。
transitions在一个feat的循环中，并不会被重复使用。它是随着tag的循环，按行(所有其它tag转移到这个tag)依次取出，然后跟forward_var的那一行直接做相加。所以我们只需要直接拿出transitions这个tag_num x tag_num的矩阵，直接跟上面stack过的forward_var直接相加，实际上就实现了之前需要tag_num次循环才能做到的事情。（记作T）
emission matrix在一个feat的循环中，只需要用到一行，因为一个feat就是一个单词呀。然后这一行是随着tag的循环，不断取出一个元素，具体使用是:重复这个元素成为一个tag_num的向量，去跟之前的forward_var、transitions的一行做相加。那么考虑一个单词，我们可以把对应的这一行转置成列向量，重复tag_num次，也形成一个矩阵。（记作E）

我们得到了这三个矩阵，直接相加。得到的矩阵的一行表示一个标签，所以我们要用torch.logsumexp(dim=1)对这个矩阵逐行进行计算，就得到了当前这个单词的分数。所以我们只需要保留外层的for feat in feats:循环就可以了，而不用再在里面写一个循环，去遍历这个单词所有可能的标签。
以上是我个人比较抽象的理解，你要想彻底想清楚还是建议去看长文详解基于并行计算的条件随机场CRF，我也因此关注了zenRRan这个大佬。如果你看完了这篇文章，或者说没有看已经理解了，那么我们就借着代码来巩固一下这个思想。

回过头来，我们来看下面这段代码:（代码参考LSTM_CRF_faster_parallell）

    def _forward_alg_new(self, feats):
        # Do the forward algorithm to compute the partition function
        init_alphas = torch.full([self.tagset_size], -10000.).to('cuda')
        # START_TAG has all of the score.
        init_alphas[self.tag_to_ix[START_TAG]] = 0.

        # Wrap in a variable so that we will get automatic backprop
        # Iterate through the sentence
        forward_var_list = []
        forward_var_list.append(init_alphas)
        for feat_index in range(feats.shape[0]):  # -1
            gamar_r_l = torch.stack([forward_var_list[feat_index]] * feats.shape[1])
            # gamar_r_l = torch.transpose(gamar_r_l,0,1)
            t_r1_k = torch.unsqueeze(feats[feat_index], 0).transpose(0, 1)  # +1
            aa = gamar_r_l + t_r1_k + self.transitions
            # forward_var_list.append(log_add(aa))
            forward_var_list.append(torch.logsumexp(aa, dim=1))
        terminal_var = forward_var_list[-1] + self.transitions[self.tag_to_ix[STOP_TAG]]
        terminal_var = torch.unsqueeze(terminal_var, 0)
        alpha = torch.logsumexp(terminal_var, dim=1)[0]
        return alpha

以上面的博客中的例子为例，即观测序列为【我去北京】，标签有三种:PN、VV、NN，我们在阅读上面博客后，可以参照上面代码，写出初始化+第一个循环的流程图:

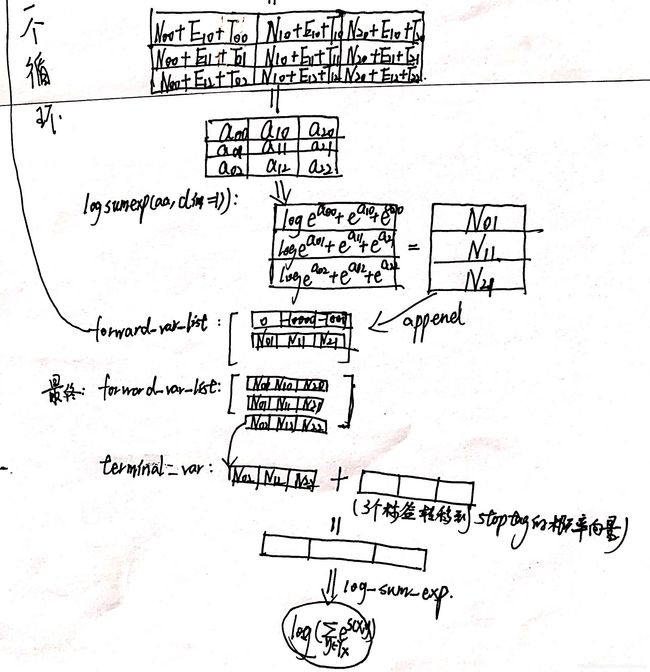
上面的计算流程中，我的三个矩阵跟zenRRan所说的三个矩阵，各自都是转置的关系(因为我是参考代码写的计算流程)，请注意。

并行化计算之batch

下面是利用并行化的思想，考虑整个batch，而不是单个句子的代码:

    def _forward_alg_new_parallel(self, feats):
    	"""
    	feats: batch_size x words x tag_num
		"""
        # Do the forward algorithm to compute the partition function
        init_alphas = torch.full([feats.shape[0], self.tagset_size], -10000.)#.to('cuda')
        # START_TAG has all of the score.
        init_alphas[:, self.tag_to_ix[START_TAG]] = 0.

        # Wrap in a variable so that we will get automatic backprop
        # Iterate through the sentence
        forward_var_list = []
        forward_var_list.append(init_alphas)
        for feat_index in range(feats.shape[1]):  # -1
        	# tag_num x batch_size * tag_num -> batch_size x tag_num xtag_num
            gamar_r_l = torch.stack([forward_var_list[feat_index]] * feats.shape[2]).transpose(0, 1)
            # gamar_r_l = torch.transpose(gamar_r_l,0,1)
            # batch_size x 1 x tag_num -> batch_size x tag_num x 1
            t_r1_k = torch.unsqueeze(feats[:, feat_index, :], 1).transpose(1, 2)  # +1
            aa = gamar_r_l + t_r1_k + torch.unsqueeze(self.transitions, 0)
            forward_var_list.append(torch.logsumexp(aa, dim=2))
        # forward_var_list[-1]: batch_size x tag_num（最后一个单词位置的，tag_num个分数）
        terminal_var = forward_var_list[-1] + self.transitions[self.tag_to_ix[STOP_TAG]].repeat([feats.shape[0], 1])
        alpha = torch.logsumexp(terminal_var, dim=1)
        return alpha

tricks:理解了单个句子，考虑增加一个batch_size这个维度的情况时，可以通过记录矩阵的维度变化来理解上述代码。

理解了batch的并行计算，那我觉得看懂CRF的代码就没有任何困难了(有困难私信或评论)。
由于LSTM_CRF_faster_parallell中，维特比解码部分的代码只写到并行化部分，我凭借我拙劣的pytorch技能对batch化的维特比解码进行了补充:

def _viterbi_decode_parallel(self, feats):
    backpointers = []
    # batch_size x tag_num
    init_vvars = torch.full((feats.shape[0], self.tagset_size), -10000.)
    init_vvars[:, self.tag_to_ix[START_TAG]] = 0
    forward_var_list = []
    forward_var_list.append(init_vvars)
    for feat_index in range(feats.shape[1]):
    	# batch_size x tag_num x tag_num
        gamar_r_l = torch.stack([forward_var_list[feat_index]] * feats.shape[2]).transpose(0, 1)
        # batch_size x tag_num x tag_num
        next_tag_var = gamar_r_l + torch.unsqueeze(self.transitions, 0)
        # batch_size x tag_num x 1 对于当前单词的每一个可能的标签，我都已经知道了转移到该标签的上一个最可能的标签
        viterbivars_t, bptrs_t = torch.max(next_tag_var, dim=-1)
        t_rl_k = feats[:, feat_index, :]
        forward_var_new = viterbivars_t + t_rl_k
        forward_var_list.append(forward_var_new)
        backpointers.append(bptrs_t)
    terminal_var = forward_var_list[-1] + torch.unsqueeze(self.transitions[self.tag_to_ix[STOP_TAG]], 0)
    # 对于最后一个单词，我选出了它最有可能的标签，以及分数
    # best_tag_id: batch_size x 1
    path_score, best_tag_id = torch.max(terminal_var, dim=-1)
    best_tag_id = best_tag_id.unsqueeze(-1)
    best_path = [best_tag_id]
    # 下面的过程理解为: bptrs_t里面记录的是，对于你最后一个单词的所有可能的标签，它的上一个最有可能的标签。那么现在，最后一个单词它已经得到了一个最有可能的标签了，所以我也需要从bptrs_t里面去取出，最有可能的那个标签的，上一个最有可能的标签。
    for bptrs_t in reversed(backpointers):
    	# bptrs_t: batch_size x tag_num
        best_tag_id = bptrs_t.gather(dim=1, index=best_tag_id)  # 一个牛逼的函数
        best_path.append(best_tag_id)
    starts = best_path.pop()
    assert (starts == torch.tensor([self.tag_to_ix[START_TAG]]).expand(feats.shape[0], 1)).all()
    best_path.reverse()
    best_path = [i.numpy() for i in best_path]  # 不然:only one element tensors can be converted to Python scalars
    best_path = torch.tensor(best_path).transpose(0, 1).squeeze()  # word_num * batch * 1 -> batch * ....
    return path_score, best_path

后记

我们回过头来思考这一句话: