海思开发：yolo v5s ：pytorch-＞onnx-＞caffe-＞nnie

一、前言

主要是遇见几个问题，赶紧记录一下，免得后面兄弟们吃同样的亏,也帮助自己记忆。附上我的 yolo v5 后处理部分 c 语言版本代码：C版 yolo v5s 后处理部分

二、转换报错

1. 报错：
Reshape dimention number shall be 2 or 4

仔细看了一下，和我 reshape 处理的数据维度有关，而转换代码里 reshape 最高支持维度数是 4。而我的数据shape 是 (1, 3, H, W, class_num + 5)，这是个五维数组。

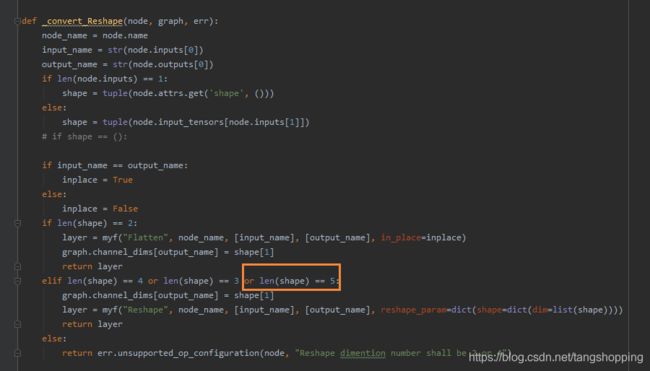
本来就想在后面加个条件 : len(shape) == 5，又怕出现新的错误，上网找了篇其他的转换代码，点进去看了下，发现内容基本一致，只不过少了个 len(shape) == 3。看完就明白可能我现在用的demo也是作者自己做了些许改动，而且他遇见的问题恐怕和我一样。于是放心的加上 len(shape) == 5
，再次运行demo。

2. 报错：
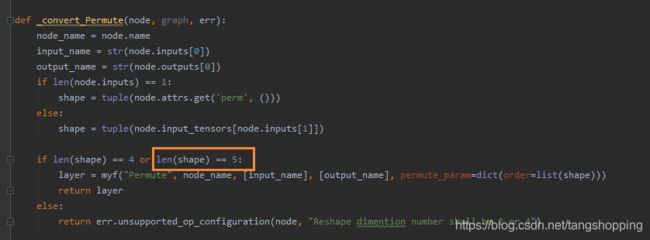
Permute dimention number shall be 2 or 4

第二个错误与上面一致，轻车熟路，在后面加个条件。

3. 报错：
Check failed: num_output_ % group_ == 0 (1 vs. 0) Number of output should be multiples of group.

具体报错如上，就是说分组卷积/分组反卷积有个硬性要求是 input_channel 与 output_channel 要是 group 的整数倍，只不过转换原因，使得这里的 output_channel 等于 1 。直接看转换的源码。

框里面的代码原本是 num_output=W.shape[1]，而我反卷积是用了分组卷积，w.shape = (512, 1, 2, 2)，这样就不对了，output num 应该是 512 才对，进行截图中的改正。再次运行，转换完成！下面跑几张图片具体看看输出值是否一致。

4. caffe 转 wk 模型报错
Permute can only support (0,1,2,3) -> (0,2,3,1) order!
reshape only support C/H/W, not N!

这两个错误不是一起出现的，犯错原因差不多，就是模型的 prototxt 文件格式不符合 nnie 要求。先说说下面一个，即 Permute 层，临时翻海思文档，描述如下：

可以看见 Permute层 局限性蛮大的，据群友们反映，这个op还挺慢的, 结合实际情况，考虑去掉它，即在 prototxt文件里删去它。

至于 reshape 层，在文档里没找见它，只能各种方法都试试，最后发现正确格式是这种。

改为下面这种格式就好了：

之后再进行转换，就没什么问题，静待模型转换完成了。

三、 其他知识点

写这个项目时，遇到的一些问题，觉得有必要和大家讲下，帮助自己记忆，也给大伙一个经验来参考。

1. reshape 的维度与海思输出数据内存分布

先看看源码的输出数据 shape 变化过程，见 yolov5/model/yolo.py 文件：

bs, _, ny, nx = x[i].shape  # x(bs, 85 * 3, 20, 20) to x(bs, 3, 20, 20, 85)
# contiguous() : https://zhuanlan.zhihu.com/p/64551412
x[i] = x[i].view(bs, self.na, self.no, ny, nx).permute(0, 1, 3, 4, 2).contiguous()

我的训练数据集是48类，则其中一个层的输出 shape 为 (1, 159, 20, 20)，其 shape 变化过程为：

#                 reshape                       permute
(1, 159, 20, 20) ---------> (1, 3, 53, 20, 20) ---------> (1, 3, 20, 20, 53)

因为python版输出数据维度过高，海思不支持，且海思 permute op 先天性限制，无法支持更多的操作，所以取消 permute 是在所难免的。但是怎样获得我们需要的 shape ，一开始想着无脑 reshape 成需要的现状，如：

#                 reshape                       reshape
(1, 159, 20, 20) ---------> (0, 3, 53, 400) ---------> (0， 3, 400, 53)
# 以上是错误操作，不要用，海思 reshape 要求输出第一维是 0 且最多维度数为 4 .

这样看起来很顺利，不过仔细想想 permute 的机制与 reshape 不一样，为此特意做了个实验：

a = torch.arange(60).view((1, 15, 2, 2)).view((1, 3, 5, 2, 2)).permute(0, 1, 3, 4, 2).contiguous()
print(a.shape)
print(a)
# output:
torch.Size([1, 3, 2, 2, 5]) # shape
# data
tensor([[[[[ 0,  4,  8, 12, 16],
           [ 1,  5,  9, 13, 17]],

          [[ 2,  6, 10, 14, 18],
           [ 3,  7, 11, 15, 19]]],


         [[[20, 24, 28, 32, 36],
           [21, 25, 29, 33, 37]],

          [[22, 26, 30, 34, 38],
           [23, 27, 31, 35, 39]]],


         [[[40, 44, 48, 52, 56],
           [41, 45, 49, 53, 57]],

          [[42, 46, 50, 54, 58],
           [43, 47, 51, 55, 59]]]]])

d = torch.arange(60).view((1, 15, 2, 2)).view((1, 3, 2, 2, 5))
print(d.shape)
print(d)
# output
torch.Size([1, 3, 2, 2, 5]) # shape
# data
tensor([[[[[ 0,  1,  2,  3,  4],
           [ 5,  6,  7,  8,  9]],

          [[10, 11, 12, 13, 14],
           [15, 16, 17, 18, 19]]],


         [[[20, 21, 22, 23, 24],
           [25, 26, 27, 28, 29]],

          [[30, 31, 32, 33, 34],
           [35, 36, 37, 38, 39]]],


         [[[40, 41, 42, 43, 44],
           [45, 46, 47, 48, 49]],

          [[50, 51, 52, 53, 54],
           [55, 56, 57, 58, 59]]]]])

虽然 shape 一样，但其数值分布完全不一样，且二者之间的数据分布没有规律可循。所以，reshape 代替 permute 的想法是错误。但我们工作总要继续，不能就此放弃。
回到主题，观察发现，python 输出的数据 shape 与海思的输出 shape 最接近的是：

#                reshape                   permute                  reshape
(1, 159, 20, 20) -----> (1, 3, 53, 20, 20) -----> (1, 3, 20, 20, 53) -----> (1, 3, 400, 53)
# python 版本输出

#                reshape                
(1, 159, 20, 20) -----> (0, 3, 53, 400) 
# 海思 版本输出

可以看见，二者已经很相像了，这样能否用呢？做个实验看下：

# 模拟 python 输出
a = torch.arange(60).view((1, 15, 2, 2)).view((1, 3, 5, 2, 2)).permute(0, 1, 3, 4, 2).contiguous().view((1, 3, 4, 5))
print(a.shape)
print(a)
# output
torch.Size([1, 3, 4, 5]) # shape
# data
tensor([[[[ 0,  4,  8, 12, 16], # 一行等于下面数组的一列
          [ 1,  5,  9, 13, 17],
          [ 2,  6, 10, 14, 18],
          [ 3,  7, 11, 15, 19]],
# ---------------------------------- anchor 
         [[20, 24, 28, 32, 36],
          [21, 25, 29, 33, 37],
          [22, 26, 30, 34, 38],
          [23, 27, 31, 35, 39]],
# ---------------------------------- anchor 
         [[40, 44, 48, 52, 56],
          [41, 45, 49, 53, 57],
          [42, 46, 50, 54, 58],
          [43, 47, 51, 55, 59]]]])

# 模拟 海思输出
b = torch.arange(60).view((1, 15, 2, 2)).view((1, 3, 5, 4))
print(b.shape)
print(b)
# output
torch.Size([1, 3, 5, 4]) # shape
# data
tensor([[[[ 0,  1,  2,  3], # 一列等于上面数组的一行，而且顺序对应的上
          [ 4,  5,  6,  7],
          [ 8,  9, 10, 11],
          [12, 13, 14, 15],
          [16, 17, 18, 19]],
# ---------------------------------- anchor 
         [[20, 21, 22, 23],
          [24, 25, 26, 27],
          [28, 29, 30, 31],
          [32, 33, 34, 35],
          [36, 37, 38, 39]],
# ---------------------------------- anchor 
         [[40, 41, 42, 43],
          [44, 45, 46, 47],
          [48, 49, 50, 51],
          [52, 53, 54, 55],
          [56, 57, 58, 59]]]])

模拟数据 shape 与实际数据 shape 一 一对应， 3 对应 3，4 对应 400， 5 对应 53 。看上文数据，虽然 shape 不一样，但是在同一个 anchor 中，模拟海思数据的一列等于模拟python数据的一行，这就有意思了。可以看见，同样几个数据，在 python 里面是按行读取，而在海思里需要按列读取。再看看海思中数据存储方式，打开海思的文档，找到内存介绍部分：

海思的模拟数 shape 是 （1, 3, 5, 4），3是通道数，上图中的 Frame0_Chn0, Frame0_Chn1，5 是height，4是 width,可以发现其与打印的数据分布是一致的，这样就可以放心的取数据了。下面是我手绘的我的输出内存分布图，觉得还是有必要说清楚，嫌啰嗦就跳过吧。

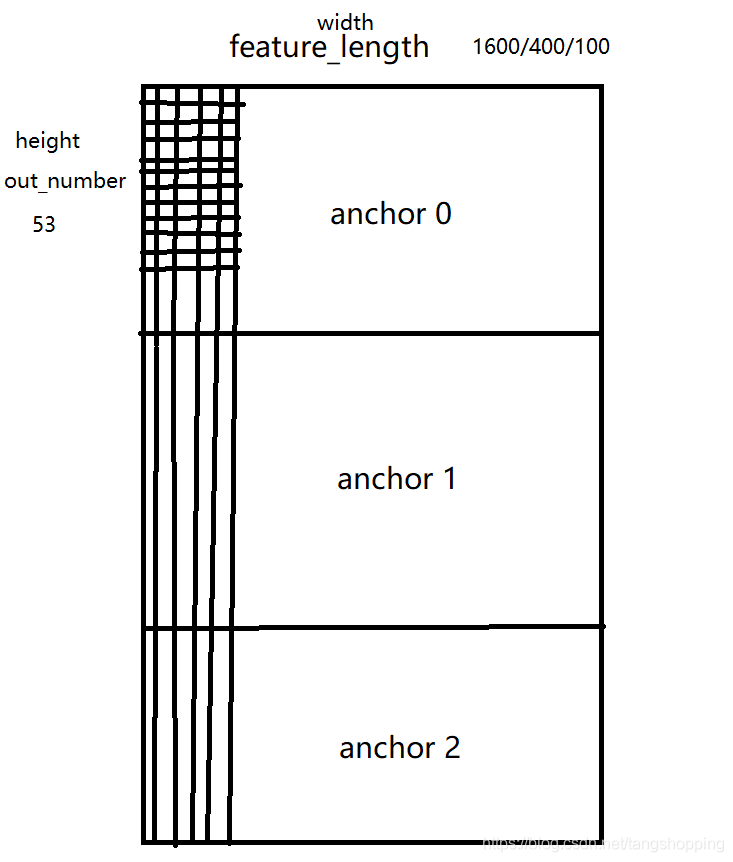
以其中一个yolo layer 输出为例，输出 shape 为（0，3, 53, 100）。3 是 anchor 数目,输出结果的内存就是被分成上中下三大部分，如我上图所示。53 就是我们需要的 bbox + confidence + class_confidence 输出，由于没有permute的原因，它们在内存中的排布是上下分布的，这与我们平常按行读取结果的习惯不一致。100是 10x10 那张 feature map 拉直后的长度，即每个 anchor 格子里有100列，每一列代表每个 grid 的数据，而每列数据中又有53行，每行代表当前 grid 中的数据输出。这样的话，再结合我的代码，应该会明白许多。

2. 网络输出处理

yolo v5 与 yolo v3 不同的是，其网络输出不同于v3的那种方式，可以看源码：

y = x[i].sigmoid()
y[..., 0:2] = (y[..., 0:2] * 2. - 0.5 + self.grid[i].to(x[i].device)) * self.stride[i]  # xy
y[..., 2:4] = (y[..., 2:4] * 2) ** 2 * self.anchor_grid[i]  # wh
x[:, 5:] *= x[:, 4:5]  # score = obj_conf * cls_conf

对于网络输出结果，先统一做 sigmoid 映射，然后x y w h 再做各自的变化，confidence 与 class_confidence 也是。

3. yolo v5 的 class 输出

因为yolo v5里面对于类别是用了多标签loss训练（不互斥多分类），即每个类别都是经 sigmoid 函数映射后输出，故不用比较大小，最后返回一个最大值对应索引。可看看源码的代码：

# Detections matrix nx6 (xyxy, conf, cls)
if multi_label:
# 注意，yolo v5 不是 softmax分类 ，所以不用遍历出概率最高的那个类别
i, j = (x[:, 5:] > conf_thres).nonzero().t()  # 只做一个阈值筛选就好
x = torch.cat((box[i], x[i, j + 5, None], j[:, None].float()), 1)

作者只做了个阈值筛选就返回所需要的类别索引，如果你说这样会不会有两个类别及以上的情况出现，对于这种，我只能说你要么模型没训练好，要么取数据出现失误，一个训练好的模型是不会的。

4. yolo v5 的 nms 处理

还是先看源码, 作者的 nms 实现简单却高效：

# 作者是先拿类别索引乘以一个较大值 max_wh（4096）
c = x[:, 5:6] * (0 if agnostic else max_wh)  # classes，5 是类别对应的索引
boxes, scores = x[:, :4] + c, x[:, 4]  # boxes (offset by class), scores
i = torchvision.ops.boxes.nms(boxes, scores, iou_thres)

作者针对每个类别都有一个 bbox偏移，在做 nms 之前，先给类别索引乘以一个较大值，再让bbox坐标值加上偏移值，这样意义是什么呢。试想每个类别都加上一个较大值，等同于每个类别都在专属于本类的坐标系里做 nms，这样做nms的时候，不用和以前一样按类别进行nms操作，而是直接做计算就行了。避免了那些 IOU>阈值 但不属于同一类的bbox被删除。
我的 demo 里没有用作者的 nms 方式，如果有兄弟实验后发现作者的更好，请告知我一声。

5. 海思版yolo v5网络修改

yolo v5一开源就看了下其结构，发现有些 op 海思不支持，所以在训练模型之初，就更改了一些，具体如下：
① 将 focus 层换成一个卷积，这个 op 海思上面不用想了(修正，自己试了下focus可以用caffe实现，海思也支持op， yolo v5 focus 层海思部署的可能性 )，欢迎各位朋友讨论；
② 将 leaky relu换成 relu，海思是支持 prelu 的，所以也支持它，不过群友们反映这个 op 很慢，输出还不稳定（这个我没有做实验，真伪性存疑），所以就干脆给它替换了；
③ 上采样层，海思支持的上采样层是 unpooling 方式，而 yolo v5里的上采样方式是最近邻插值（nearest），鉴于各种因素考虑，还是把它换成了分组转置卷积（分组这里要注意，yolo v5 网络其实大部分卷积都是深度卷积 + 逐点卷积，所以转置卷积也分组吧）；
④ spp 层的 maxpool ceil mode 都是默认的 false 状态，而海思里的 caffe 只支持 ceil mode 方式，所以要改成 ceil mode = True 。一开始忘记打开使得输出bbox明显偏大（不敢确认是这个的原因），后来特意停止训练修改该参数，再继续训练，后来发现 bbox 正常了。

三、后言

仓促之下写成，如有不好之处，还请指出，谢谢。

四、致歉

在此说声抱歉，由于我的粗心与愚蠢，使得我自己包括其他兄弟的输出结果不正常，给一些兄弟带来很大麻烦。

类似上面这种问题，中途有兄弟也询问过是不是我后处理代码有误，可是在我再一次粗心下，没有发现。在最近一位兄弟的指正下，终于找到了这个错误，gitee仓库的代码已经修改，而且经一位网友验证，修改后模型输出结果能用！
这次给我的教训是：遇事多往自己身上找原因，人总是喜欢把失败归咎于别人，把成功归功于自己。