数据结构课程设计(逆波兰设计 报告+代码)
1.实验内容与要求
1.1 实验内容
逆波兰表达式又叫做,是波兰逻辑学家 J・卢卡西维兹于 1929 年首先提出的 一种表达式的表示方法。采用这种表达式组织逻辑提问非常方便检索运算,所以这种方法最 早用于情报检索。不同于通常的中缀表达式,逆波兰表达式把操作数写在前面,操作符写在 后面,所以也称为后缀表达式。请采用相应的数据结构实现中缀表达式转换成逆波兰表达式, 并实现逆波兰表达式的计算,要求能够支持加、减、乘、除、取余、指数和括号等运算。
1.2 实验要求
- 要求采用链表来实现栈,不允许使用标准模板类的链表类(list)、栈类(stack)和函数;
- 要求支持加、减、乘、除、取余、指数和括号等运算;
- 实现中缀表达式转换成逆波兰表达式的功能时,要求输出显示能够清楚地显示出的整个 转换过程,包括压栈和出栈过程;
- 实现逆波兰表达式的计算功能时,要求输出显示能够清楚地显示出的整个计算过程,包 括压栈和出栈过程;
- 要求采用类的设计思路,不允许出现类以外的函数定义,但允许友元函数。主函数中只 能出现类的成员函数的调用,不允许出现对其它函数的调用。
- 要求采用多文件方式:.h 文件存储类的声明,.cpp 文件存储类的实现,主函数 main 存 储在另外一个单独的 cpp 文件中。如果采用类模板,则类的声明和实现都放在.h 文件中。
- 不强制要求采用类模板,也不要求采用可视化窗口;要求源程序中有相应注释;
- 建议采用 Visual C++ 6.0 及以上版本进行调试;
2.设计思路设计
该设计主要分为两部分,一部分是实现中缀表达式转为后缀表达式;另一部分是实现后缀表达式的计算。实现第一个功能采用栈(存字符串)的结构,将输入的每个字符进行判断等操作,取用两个栈,一个存运算符,另一个存每一步转化过程的不完整表达式,最终输出结果。第二个功能也采用栈(存数字结果)的结构进行辅助,对每个输入的字符进行判断,将最终结果存入栈中
2.1 系统总体设计
- 利用链表的功能与定义,设计两个stack类,分别命名为Mystack 与Mystack1。将两个链表设计得与STL中的栈的功能大体相似,这两个栈的区别为,Mystack类存储数学结果(双精度浮点数),Mystack1类存储字符串。
- 在实现后缀表达式的计算时,将输入的字符一个个进行判断,若判断为数字,将这个浮点数提取出来,再存入到Mystack类的栈中,若遇到运算字符,在栈取两个数任然不为空的情况下,取出两个浮点数,进行相应的运算操作,并且将新的结果压入栈中。
2.2 系统功能定义
| 功能描述 |
输入 |
输出 |
备注 |
| 计算后缀表达式 |
一个字符串 |
计算结果的数值 |
涉及加、减、乘、除、取余、取幂运算 |
| 中缀后缀表达式 |
一个字符串 |
计算结果的字符串 |
涉及加、减、乘、除、取余、取幂运算 |
| 判错机制 |
判断过程是否发生错误 |
贯穿在上两个功能之间 |
2.3 算法设计
2.3.1计算后缀表达式
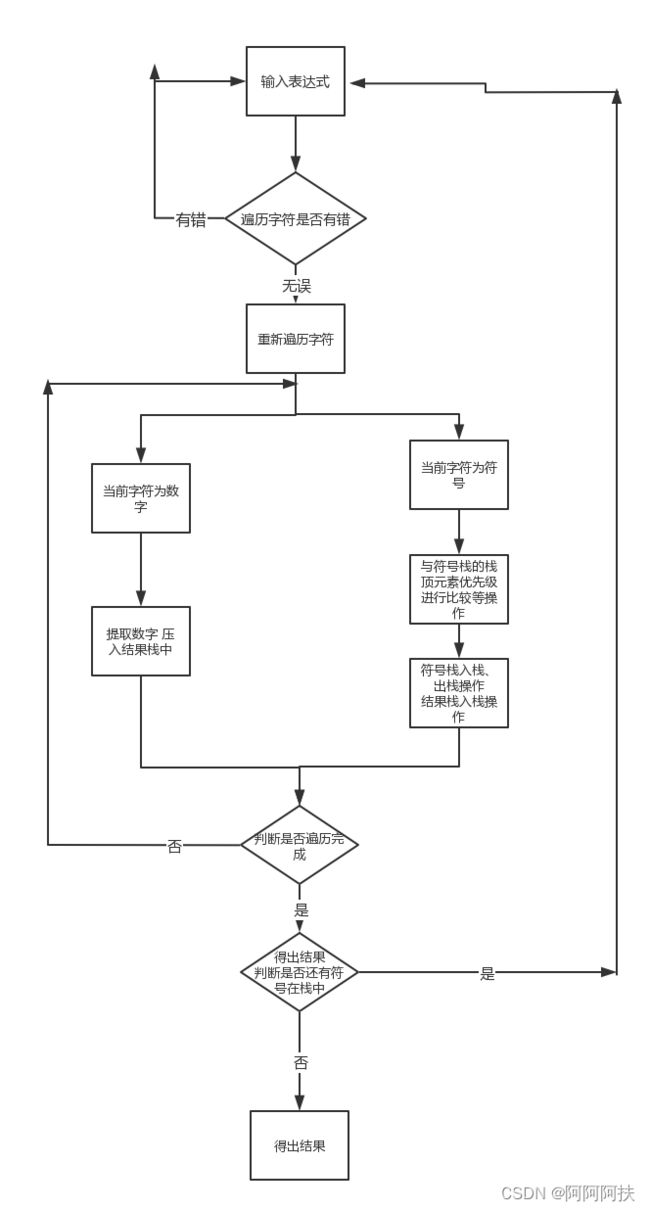
首先采用流程图的形式描述算法,计算后缀表达式的流程如下图所示。
算法文字描述
首先我们需要一个stack类来存放我们一步步计算得到的结果,用链表来建立这个结构在实现计算后缀表达式的功能中,最重要的就是提取出输入的数字字符与运算符字符。该功能执行的第一步是初步判断输入的表达式是否含有除运算符、数字字符、空格和小数点之外的字符,如果存在这种不合法的字符,则立刻报错,不进行任何的计算(出栈、入栈等操作)。如果没有发现这样的字符,则开始计算。
计算采用遍历判断结构,若判断出该字符是一个数字字符,则程序进行提取数字操作。具体实现过程为:
(1)若当前的字符任然为数字,则进行多位数提取操作(sum=sum*10+i类似这样的操作),继续往下遍历整个字符串,直到遇到字符不是数字和小数点的才停止。
- 如果判断出当前的字符为小数点,则保持前面计算出的sum即小数点前的
数值不变,使用pow函数来进行小数点后的提取(若当前是小数点一位,则计算sum=sum+pow(10,-pos)*i),持续做这样的操作,继续遍历字符串,直到遇到的字符不是数字字符为止(即该数字提取完毕)提取完毕数字之和,将数字的数值压入自己定义的栈中,等待计算。
如果当前的字符是运算符
- case:“+”遇到加号,对栈分别进行两次判断空操作,若提取两个数字仍不为空,则将这两个数进行加法运算,并将运算的结果存入栈中。若出现为空的情况,则程序报错,退出计算,并要求重新输入后缀表达式。
- Case:“-”遇到减号,对栈分别进行两次判断空操作,若提取两个数字仍然不为空,则将这两个数进行减法运算,并将运算的结果存入栈中。若出现为空的情况,则程序报错,退出计算,并要求重新输入后缀表达式。
- Case:“*”遇到乘号,对栈分别进行两次判断空操作,若提取两个数字仍然不为空,则将这两个数进行乘法运算,并将运算的结果存入栈中。若出现为空的情况,则程序报错,退出计算,并要求重新输入后缀表达式。
- Case:“/”遇到除号,对栈分别进行两次判断空操作,若提取两个数字仍然不为空,并且除数不为0,则将这两个数进行除法运算,并将运算的结果存入栈中。若出现为空或者除数为0的情况,则程序报错,退出计算,并要求重新输入后缀表达式。
- Case:“%”遇到取余符号,对栈分别进行两次判空操作,若提取两个数字仍然不为空,则将这两个数提取出来,提取之后,判断该数是否为整数,若这两个数都是整数,则进行取余运算,若有一个或者两个都是浮点数,则程序会进行提示小数无法进行取余运算,程序报错,退出计算,并要求重新输入后缀表达式
- Case:“^”遇到取幂符号,对栈分别进行两次判空操作,若提取两个数字仍然不为空,则将这两个数进行取幂运算,并将运算的结果存入栈中。若出现为空的情况,则程序报错,退出计算,并要求重新输入后缀表达式。
- Case:“ ”遇到空格的话,不进行任何多余的操作,直接continue
一个个判断,直到判断遍历字符串完成,得出一个最后的结果。当然,得到这个结果之后,还要对栈的size进行判断,如果后缀表达式输入无误的话,栈里面只有一个数值,若栈的size不为1,则可以断定输入的表达式是不合法的,则程序进行报错,结束计算,并要求重新输入后缀表达式。
2.3.2 实现中缀表达式转后缀
下图为该功能的流程图
中缀转后缀算法文字描述
报错机制(计算这个后缀表达式)
首先实现这个我们需要一个辅助站来存一个个字符,这里仍然使用链表,建立一个简单的stack类,与上面的很相似,只是存储的数据类型不一样。上面储存的是数值类型,这里储存的是字符类型。
运算符优先级 ^ > * / % > + - 并且左括号等级最低。
该功能执行的第一步也是判断输入的字符串是否存在不合法的字符(除数字、运算符、空格、小数点、括号的字符)如果存在这样的不合法字符,程序直接提示错误,并且要求重新输入中缀表达式。如果该字符串合法的话,则开始执行中缀转后缀的操作。
转换操作总体结构就是遍历字符串。同时,这里需要两个stack类来作为辅助栈,一个存储遇到的符号,下面简称为符号栈。一个存储一步步得到的后缀表达式,下面简称为结果栈。
如果遇到的是数字字符,则开始提取数字的操作(即一个循环)。将数字字符压入栈中,往下继续遍历字符串,将该字符压入栈中,若遍历中遇到了一个不是小数点字符也不是数字字符的字符,就结束字符的入栈循环,并在结果栈中加入一个空格来分割这些表达式。
如果遇到的是运算符,则开始运算符优先级比较以及出栈、入栈操作。具体实现过程如下:
- case:“(”如果遇到的是左括号,则将左括号压到符号栈中。
- Case:“)”如果遇到的是右括号,则对符号栈里的符号进行遍历,持续弹出里面的运算符,直到遇到“(”为止,没遇到之前,一直持续弹出,并将这些元素全都压入结果栈中。
- Case:“+”||“-”如果遇到的加号或者减号(“+”“-”优先级运算符里优先级最低),如果栈顶元素不是“(”(优先级为0),并且栈不为空,则一直执行栈顶元素出栈,并压入结果栈中操作,当栈为空时或者遇到“(”,将“+”“-”符号压入符号栈,继续往下遍历字符串。
- Case:“*”||“/”||“%”如果遇到的是乘号、除号、取余运算(三个符号优先级相同,次高),如果栈顶元素是同级或者高级运算符(* / % ^ 运算符)在栈不为空的情况下,不断对符号栈进行栈顶元素出符号栈、入结果栈的操作,直至不满足条件,退出循环为止。
- Case:“^”在以上这些运算符中是相对最高级的,因此,只要遇到取幂运算,便将该符号压入符号栈中,接着遍历字符串。
- 如果遇到的是空格,则不执行任何操作,直接进行下一个字符判断。
等到程序遍历完字符串之后,首先进行一个简单的判断,查看符号栈中是否还有元素存在,若还有符号没有出栈,则该表达式一定是有误的,程序就会直接提示表达式有误,要求重新输入。当然,并不是栈为空,则该表达式就正确了,下面讲一下这个程序的报错机制。
2.3.3 报错机制
首先,中缀转后缀的错误是相对没有那么容易发现的,因为只涉及到出栈、入栈等操作,即使你输入的表达式有误,如果程序到这里为止,依然能得到一个看似“正确”的结果。但是,像上面那个计算后缀表达式,是比较容易及时判断出错误的,所以,判断中缀表达式输入是否正确,我们先把这个中缀表达式转换成后缀表达式,若转化不成功,则该表达式必定有错,若转换成功,则对这个后缀表达式进行计算,如果能够得到正确结果,则说明这个中缀表达式是正确的,同时,输出result栈中的表达式;如果不行,则该表达式就是错误的,程序进行提示,并且要求重新输入中缀表达式,这就是这个程序的报错机制。如果没有错的话,在得到正确的后缀表达式的同时,我们还可以得到这个中缀表达式的计算结果。
下面是报错机制的流程图
3.功能实现
3.1 类 1
采用表格的形式描述类的定义和功能
类名称:MYstack
功能: 作为辅助栈,存储后缀表达式的计算结果
class Node {//定义一个节点,构造链表结构
public:
double data; Node *next;
Node(double x1, Node *nex) :data(x1), next(nex) {
}
Node(double x1) :data(x1), next(0) {
}
};
class Mystack {
private:
Node *first;
int size;
public:
Mystack() :first(0), size(0) {//无参构造函数
}
Mystack(const Mystack&s);//拷贝构造函数
~Mystack();//析构函数
int getsize();//返回栈中的数据个数
void push(double x);//压入栈操作
void pop();//删除栈顶元素
void print();//打印结果
Node* top();//提取栈顶元素
friend void caculate(string str);//计算后缀表达式
bool isempty();//判断栈是否为空
friend bool calculatecopy(string str);//判断由中缀表达式转化而来的后缀表达式能否计算正确
}3.2 类 2
类名称:MYstack1
功能: 作为辅助栈,存储运算符与转化的后缀表达式
class Node1 {//定义节点,指向char类型数据
public:
char data; Node1 *next;
Node1(char dat, Node1 *nex = 0) :data(dat), next(nex) {
}
};
class Mystack1 {//类的定义
private:
Node1 *first;
int size;
public:
Mystack1() :first(0), size(0) {//无参构造函数
}
Mystack1(const Mystack1&s);//拷贝构造函数
~Mystack1();//析构函数
void push(char x);//将字符压入栈中
void pop();//删除栈顶元素
void print();//打印该表达式
char top();//得到栈顶元素
bool empty();//判断栈是否为空
friend void exchange(string str);//将中缀表达式转化成后缀表达式
};4.功能截图
4.1 中缀表达式转后缀运行截图
1.只涉及个位数的转换
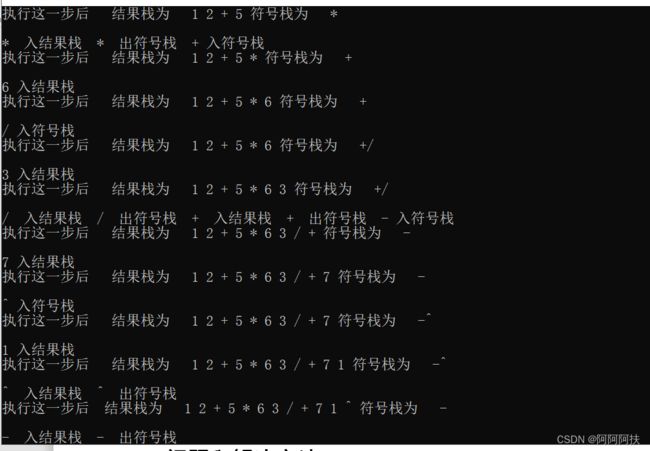
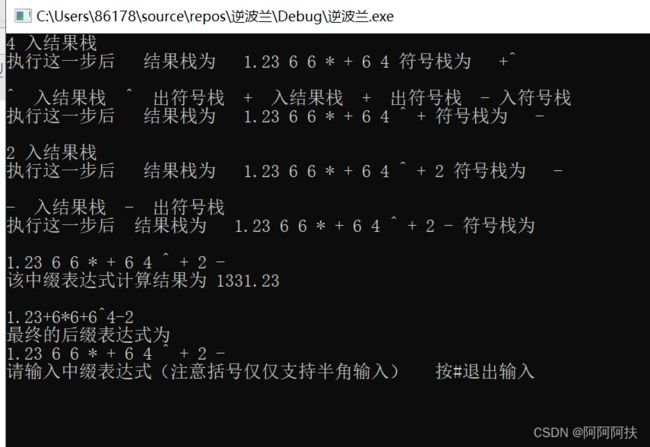
下图为输出表达式(1+2)*5+6/3-7^1的计算过程,第一遍输出该表达式时,程序之所以报错是因为,该计算器仅仅支持半角输入的括号,如果输入了全角的括号,改程序不认识这个字符,就会告诉操作者在4这个位置输入了不合法字符。第一次输入时,因为输入的括号不是半角下的,程序无法识别,就会报错,提醒重新输入。重新输入后,进行表达式的计算,并且会输出一步步运行的过程。这其中,结果栈用来保存最后的结果,符号栈用来存储表达式中的符号,在程序经过判断后,在合适的时候出栈,并压入结果栈中。
下面输入一个中缀表达式进行程序功能的演示,输入的式子为(1+2)*5+6/3-7^1
如果自己转换一遍的的话结果为 1 2 + 5 * 6 3 / + 7 1 ^ -
因为每执行一步,就会有结果栈和符号栈的变化,所以输出的步骤会比较长。
如图,我们已经得到了一个转换后的结果,但是,如果我们输入的表达式有误,并且那些潜在错误会避开判错程序,那个依然可以得到一个看似正确的结果。为了防止输入的表达式有错,对转换得到的后缀表达式进行计算,若能得到正确的计算结果,则输出该结果,并且将正确的后缀表达式输出。程序一边计算,一边显示出栈、入栈的具体过程
2.浮点数及多位整数的转化
浮点数的中缀转后缀(主要是提取数字的过程多了一些),过程与上面类似。
下面的是浮点数有关的具体的转化过程。
如果输入了不合法的字符,程序直接报错。
3.可以转化出来,但是本身表达式就存在错误
譬如说下面这个式子(1+2)*8+ 按照中缀转后缀的规则,的确是可以得到这样一个结果1 2 + 8 * +,但是我们自己判断一下,这个式子本身就是错误的,本身应该是无法转换的,因此,将转换后的式子拿去计算,我们发现得不出正确的结果,即可判断该式错误。
同理,下面这个是除数为0程序也会进行提醒,不能转换
4.2 计算后缀表达式功能运行截图
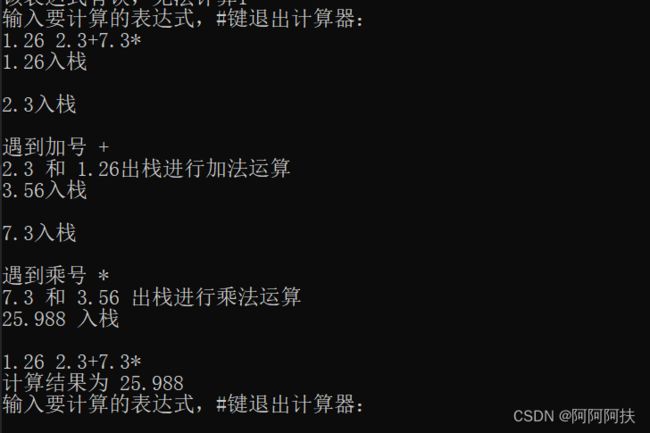
1.输入一个合法的表达式
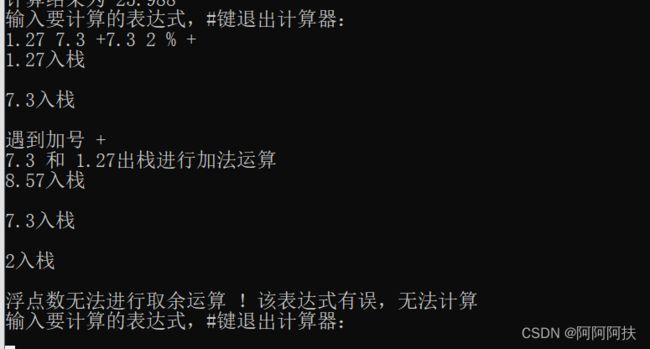
浮点数不能进行取余运算,遇到这样的式子,程序会报错,例如下面这个式子,按常理的话,应该是这样计算的 1.27+7.3+7.3%2 但是7.3不是整数,无法进行取余运算,运行时,会报错。
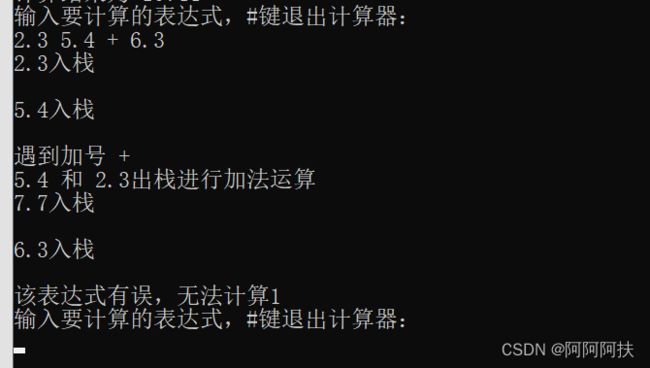
还有一种表达式有误,就是运算不够或者数字不够,运行的时候,如果是数字不够,则对栈进行判空的操作时,就会报出错误,如果是数字过多、运算符少,则最后的栈里面的值肯定不止一个,对栈的大小进行判断之后,会报出错误,就如下图所示。
运算的时候,除数为0则直接报错。
5.问题和解决方法
5.1 多位数无法进行计算
| 问题描述:刚编写程序时,只能进行个位数的计算 |
| 解决方法:改变遍历时遇到数字操作,原本遇到数字就把数字压入栈中,实际上,我们如果遇到数字,就应该继续遍历字符串,将后面所有的数字字符提取出来,将这些数字字符进行整合,并将最后这个结果压入到栈中,这样就可以把多位整数加入到栈中,可以实现后缀表达式中,存在多位整数的计算。 |
5.2 浮点数无法计算
| 问题描述:继续上面那个问题,解决完这个多位整数的计算之后,想到还有浮点数的计算无法完成 |
| 解决方法:还是继续完善提取数字的功能,上文中,提取所有的整数之后,如果有遇到小数点,则把小数点后面的数字提取出来,记录小数点的位置,用pow函数进行计算小数点后的数值,最后将得到的结果压入栈中。 |
5.3 无法准备判断表达式输入有误
| 问题描述:无法判断表达式的正误 |
| 解决方法:该程序,如果只是要执行计算后缀表达式和将中缀表达式转为后缀表达式,在保证输入的表达式都是正确的情况下,实现这个功能是十分简单的,但是,用户输入时,总会会一些错误表达式,若不加判断错误的程序,那很有可能在输入的表达式错误的情况下,仍然得到一个表达式或者一个计算结果,显然这样的过程是存在逻辑错误的。所以,在这个程序里面加入判错机制是非常有必要的。本程序主要是在计算后缀表达式的过程中,一边计算,一边判断错误的,如果表达式存在错误,则就会产生存储计算结果的栈在计算时,栈为空的情况,或者除数为0,浮点数取余等等不应该发生的情况,经过这样的程序判错后,可以大大削减表达式出现错误程序却仍然计算的情况发生的可能性,尽可能保证程序的逻辑正确性。对于一个中缀表达式,因为计算机其实是看不懂中缀表达的,我们如果要在中缀转后缀的过程中,对表达式的正误进行判断,是非常繁琐并且很困难,所以,这里采用的是先把这个中缀表达式(不论正误)转化成后缀表达式,再将这个后缀表达式,进行一个计算(与上述描写的过程一致),若能得到一个正确结果,就将该表达式的计算结果输出,并得到该表达式转化成后缀表达式的结果,将其输出。 |
6.源代码
Mystack.h
#pragma once
#ifndef MYSTACK_H
#define MYSTACK_H
#include
#include
#include
#include
using namespace std;
class Node {
public:
double data; Node *next;
Node(double x1, Node *nex) :data(x1), next(nex) {
}
Node(double x1) :data(x1), next(0) {
}
};
class Mystack {
private:
Node *first;
int size;
public:
Mystack() :first(0), size(0) {
}
Mystack(const Mystack&s);
~Mystack();
int getsize();
void push(double x);
void pop();
void print();
Node* top();
friend void caculate(string str);
bool isempty();
friend bool calculatecopy(string str);
};
#endif Mystack.cpp
#include"Mystack.h"
using namespace std;
bool Mystack::isempty() {
if (size == 0)return true;
else return false;
}
int Mystack::getsize() {
return size;
}
Mystack::Mystack(const Mystack&s) {
Node *h, *q, *temp1;
this->first = s.first;
h = s.first;
while (h)
{
if (first != 0) {
h->next = first; first = h;
}
else { first = h; first->next = 0; }
h = h->next;
}
}
Node* Mystack::top() {
return first;
}
void Mystack::push(double x) {
Node *p = new Node(x);
p->next = first; first = p;
//入栈即在这个链表的最前面添加节点
size++;
}
void Mystack::pop() {
if (first) {//栈不为空
Node *p = first;
first = first->next;//删除栈的top值即删除链表的第一个节点
size--;//数量--
delete p;
}
else return;
}
Mystack::~Mystack() {
Node*p1 = first;
Node *p2 = p1;
while (p1 != 0) {
p2 = p1;
p1 = p1->next;
delete p2;
}
delete p1;
}
void Mystack::print() {
Node*p1 = first;
while (!p1) {
cout << p1->data << " ";
p1 = p1->next;
}
}Mystack1.h
#pragma once
#ifndef MYSTACK1_H
#define MYSTACK1_H
#include
#include
#include
#include
#include
#include
using namespace std;
class Node1 {
public:
char data; Node1 *next;
Node1(char dat, Node1 *nex = 0) :data(dat), next(nex) {
}
};
class Mystack1 {
private:
Node1 *first;
int size;
public:
Mystack1() :first(0), size(0) {
}
Mystack1(const Mystack1&s);
~Mystack1();
void push(char x);
void pop();
void print();
char top();
bool empty();
friend void changeback(string str);
};
#endif Mystack1.cpp
#include"Mystack1.h"
bool Mystack1::empty() {
if (first == 0)return true;
else return false;
}
Mystack1::Mystack1(const Mystack1&s) {
Node1 *h;
this->first = s.first;
h = s.first;
while (h)
{
if (first != 0) {
h->next = first; first = h;
}
else { first = h; first->next = 0; }
h = h->next;
}
}
char Mystack1::top() {
return first->data;
}
void Mystack1::push(char x) {
Node1 *p = new Node1(x);
if (first == 0) { first = p; first->next = 0; }
else { p->next = first; first = p; }
//入栈即在这个链表的最前面添加节点
}
void Mystack1::pop() {
if (first) {//栈不为空
Node1 *p = first;
first = first->next;//删除栈的top值即删除链表的第一个节点
size--;//数量--
delete p;
}
else return;
}
Mystack1::~Mystack1() {
Node1*p1 = first;
Node1 *p2 = p1;
while (p1 != 0) {
p2 = p1;
p1 = p1->next;
delete p2;
}
delete p1;
}
void Mystack1::print() {
Node1*p1 = first;
char s1;
string sum = "";
while (p1 != 0) {
s1 = p1->data;
sum = s1 + sum;
p1 = p1->next;
}
cout << sum;
}主函数
// 逆波兰.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
#include"Mystack1.h"
#include"Mystack.h"
#include
using namespace std;
void caculate(string str) {
Mystack s;
int k = str.length();
int i = 0;
double x;
int flag = 1;
while (i < k&&flag == 1) {//遍历字符串
if (str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/' || str[i] == '^' || str[i] == '%')//当前的是运算符,取栈顶两个元素进行相应的操作,将结果压入栈中
{
double num1, num2;
switch (str[i])//判断该字符是运算符还是数字
{
case '+':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;
s.pop();
x = num1 + num2;
s.push(x);//把计算的结果压入栈中
cout << "遇到加号 + " << endl;//描述具体过程
cout << num1 << " 和 " << num2 << "出栈进行加法运算 " << endl;
cout << x << "入栈" << endl << endl;
break;
case '-':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;;
s.pop();
x = num2 - num1;
s.push(x);
cout << "遇到减号 - " << endl;
cout << num1 << " 和 " << num2 << " 出栈进行减法运算 " << endl;
cout << x << " 入栈 " << endl << endl;
break;
case '*':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;
s.pop();
x = num1 * num2;
s.push(x);
cout << "遇到乘号 * " << endl;
cout << num1 << " 和 " << num2 << " 出栈进行乘法运算 " << endl;
cout << x << " 入栈" << endl << endl;
break;
case '/':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;
s.pop();
if (s.isempty() || num1 == 0) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;
s.pop();
x = num2 / num1;
s.push(x);//将相除的运算的结果压入栈中
cout << "遇到除号 / " << endl;
cout << num1 << " 和 " << num2 << "出栈进行除法运算 " << endl;
cout << x << " 入栈 " << endl << endl;
break;
case '^':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;
s.pop();
x = pow(num2, num1);
s.push(x);//将取幂的结果压入栈中
cout << "遇到指数符号 ^ " << endl;
cout << num1 << " 和 " << num2 << "出栈进行取幂运算 " << endl;
cout << x << " 入栈 " << endl << endl;
break;
case'%':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return;
}
num2 = s.top()->data;
s.pop();
int temp1 = (int)num1;
int temp2 = (int)num2;
if ((temp1 - num1) != 0 || (temp2 - num2) != 0) {//进行取余运算的两个数不是整数,不合逻辑
cout << "浮点数无法进行取余运算 !该表达式有误,无法计算" << endl;
return;
}
x = temp2 % temp1;
s.push(x);
cout << "遇到取余符号 % " << endl;
cout << num1 << " 和 " << num2 << "出栈进行取余运算 " << endl;
cout << x << "入栈" << endl << endl;
break;
}
}
else if (str[i] == ' ') { i++; continue; }
else if (str[i] >= '0'&&str[i] <= '9') {//遇到数字,开始数字提取
double x = 0;
double y = 0;
while (((str[i] >= '0'&&str[i] <= '9') || str[i] == '.') && i < k) {//一直都是数字
if (str[i] != '.') x = x * 10 + int(str[i]) - 48;//没有遇到小数点,对整数部分进行提取
else {//遇到小数点,对小数点后的数值进行相加
i = i + 1;
while ((str[i] >= '0'&&str[i] <= '9') && i < k) {
y++;//变量y相当于记录小数点后几位
x = x + (int(str[i]) - 48)*pow(10.0, -y);
i++;
}
break;
}
i++;
}
s.push(x);//将提取出的数字压入栈中
cout << x << "入栈" << endl << endl;
continue;
}
i++;
}
if (s.getsize() != 1) {//最后栈的结果不唯一,或者为空
cout << "该表达式有误,无法计算4" << endl;
}
else {//计算无误
double y = s.top()->data;
cout << str << endl;
cout << "计算结果为 " << y << endl;//得出正确的结果
}
}
bool calculatecopy(string str) {//判断由中缀转后缀的表达式能否进行计算,即判断该表达式的正确与否
Mystack s;
int k = str.length();
int i = 0;
double x;
int flag = 1;
while (i < k&&flag == 1) {//遍历字符串
if (str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/' || str[i] == '^' || str[i] == '%')//当前的是运算符,取栈顶两个元素进行相应的操作,将结果压入栈中
{
double num1, num2;
switch (str[i])
{
case '+':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false;
}
num2 = s.top()->data;
s.pop();
x = num1 + num2;
s.push(x);
break;
case '-':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num1 = s.top()->data;;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num2 = s.top()->data;;
s.pop();
x = num2 - num1;
s.push(x);
break;
case '*':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num2 = s.top()->data;
s.pop();
x = num1 * num2;
s.push(x);
break;
case '/':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num2 = s.top()->data;
s.pop();
x = num2 / num1;
s.push(x);
break;
case '^':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num2 = s.top()->data;
s.pop();
x = pow(num2, num1);
s.push(x);
break;
case'%':
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false ;
}
num1 = s.top()->data;
s.pop();
if (s.isempty()) {//栈里面的元素不足,无法进行运算
cout << "该表达式有误,无法计算" << endl;
return false;
}
num2 = s.top()->data;
s.pop();
int temp1 = (int)num1;
int temp2 = (int)num2;
if ((temp1 - num1) != 0 || (temp2 - num2) != 0) {
cout << "浮点数无法进行取余运算 !该表达式有误,无法计算" << endl;
flag = 0;
return false;
}
x = temp2 % temp1;
s.push(x);
break;
}
}
else if (str[i] == ' ') { i++; continue; }
else if (str[i] >= '0'&&str[i] <= '9') {//提取数字,和上面是一样的操作
double x = 0;
double y = 0;
while (((str[i] >= '0'&&str[i] <= '9') || str[i] == '.') && i < k) {
if (str[i] != '.') x = x * 10 + int(str[i]) - 48;
else {
i = i + 1;
while ((str[i] >= '0'&&str[i] <= '9') && i < k) {
y++;
x = x + (int(str[i]) - 48)*pow(10.0, -y);
i++;
}
break;
}
i++;
}
s.push(x);
continue;
}
i++;
}
if (s.getsize() != 1) {
cout << "该表达式有误,无法计算" << endl;
return false;
}
else {
double y = s.top()->data;
cout << str << endl;
cout << "该中缀表达式计算结果为 " << y << endl;//可以得到一个正确的计算的结果,即该表示正确
return true;
}
}
void changeback(string str) {//中缀转后缀表达式
Mystack1 stk;
Mystack1 result;
char temp;
for (int i = 0; i < str.length(); i++) {//一个个提取字符
int flag = 0;
while (str[i] >= '0'&&str[i] <= '9') {//提取数字
result.push(str[i]); flag = 1;
cout << str[i] << " 入结果栈 ";
i++;
if (str[i] == '.') {
result.push(str[i]);
cout << str[i] << " 入结果栈 ";
i++;
}
}
if (flag == 1) {
i--;
result.push(' ');//用空格将表达式分开,避免无法区分数字
}
if (str[i] == '+' || str[i] == '-') {//遇到加号、减号两个运算符较低的
while (1) {
if (!stk.empty() && stk.top() != '(') {//如果栈不为空,或者不是最低级的左括号运算符则将栈顶元素弹出
temp = stk.top();
cout << temp << " 入结果栈 ";
cout << temp << " 出符号栈 ";
result.push(temp);
result.push(' ');
stk.pop();
}
else {//栈为空或者遇到左括号(运算级别最低的运算符)
cout << str[i] << " 入符号栈 ";
stk.push(str[i]);
break;
}
}
}
else if (str[i] == '*' || str[i] == '/' || str[i] == '%') {//* / %这三个运算符运算级别相同
while (1) {//遇到是同级或者更高级的运算符
//将原本栈中的元素弹出,压到结果栈中
if (!stk.empty() && (stk.top() == '*' || stk.top() == '/' || stk.top() == '%' || stk.top() == '^')) {
temp = stk.top();
cout << temp << " 入结果栈 ";
cout << temp << " 出符号栈 ";
result.push(temp);
result.push(' ');
stk.pop();
}
else {//遇到的是低级的运算符
cout << str[i] << " 入符号栈 ";
stk.push(str[i]);
break;
}
}
}
else if (str[i] == '^') {//遇到了最高级的运算符,直接压入符号栈中
cout << str[i] << " 入符号栈 ";
stk.push(str[i]);
}
else if (str[i] == '(') {
stk.push(str[i]);
cout << str[i] << " 入符号栈 ";
}
else if (str[i] == ')') {//遇到右括号,除非遇到左括号,持续弹出符号栈栈顶元素
while (1) {
while(stk.top() != '(') {
temp = stk.top();
cout << temp << " 入结果栈 ";
cout << temp << " 出符号栈 ";
result.push(temp);
result.push(' ');
stk.pop();
}
stk.pop(); //删除'('
break;
}
}
cout << endl;
cout << "执行这一步后 " ;
cout << "结果栈为" << " "; result.print();
cout << "符号栈为" << " "; stk.print();
cout << endl << endl;
}
while (!stk.empty()) {//符号栈不为空,将所有符号弹出
temp = stk.top();
cout << temp << " 入结果栈 ";
cout << temp << " 出符号栈 ";
result.push(temp);
result.push(' ');
stk.pop();
cout << endl;
cout << "执行这一步后 ";
cout << "结果栈为" << " "; result.print();
cout << "符号栈为" << " "; stk.print();
cout << endl << endl;
}
Node1*p1 = result.first;
char s1;
string sum = "";
while (p1 != 0) {
s1 = p1->data;
sum = s1 + sum;
p1 = p1->next;
}//得到该后缀表达式,因为无法确定该式是否正确,下面对其进行计算判断
if (calculatecopy(sum) == true) {
cout << endl;
cout << str;
cout << endl << "最终的后缀表达式为" << endl;
cout << sum;
cout << endl;
}
else {
cout << "该式通过计算不能得到正确结果" << endl;
cout << "请输入一个正确的表达式";
}
}
int main()
{
int dd = 1;
int s;
int k;
int chance;
cout << endl;
cout << endl;
cout << endl;
cout << " ==============================================="<> chance) {
if (chance == 1) {
string str;
system("cls");//
cout << endl << endl << endl;
cout << " ==================欢迎进入中缀转后缀功能区==================="<= 45 && a <= 57) || a == 42 || a == 43 || a == 37
|| a == 32 || a == 40 || a == 41||a==94))//
{
flag = 0;
cout << i << " " << str[i] << " ";
cout << "该表达式输入了无法解析的字符 表达式有误 请重新输入" << endl;
cout << "若要退出该功能请按#" << endl;
break;
}
}
if (flag == 0)continue;
changeback(str);//
cout << "==============================================================================";
cout << endl<= 45 && a <= 57) || a == 42 || a == 43 || a == 37 || a == 32 || a == 94))//根据运算符的ASC码来判断是否有不合法的
{
flag = 0;
cout << " 在 " << i << " 这个位置 " << str1[i] << " ";
cout << "该表达式输入了无法解析的字符 表达式有误 请重新输入" << endl;
cout << "若要退出该功能请按#"<