跟我一起学scikit-learn18：决策树算法

决策树（Decision Tree，简称DT）是最经典的机器学习模型之一，它的预测结果容易理解，易于向业务部门解释，预测速度快，可以处理离散型数据和连续型数据。

1.决策树算法原理

决策树是一个类似于流程图的树结构，分支节点表示对一个特征进行预测，根据预测结果进行分类，叶子节点代表一个类别。如下图所示，我们用决策树来决定下班后的安排：

我们分别对精力指数和情绪指数两个特征进行测试，并根据测试结果决定行为的类别。每选择一个特征进行测试，数据集就被划分成多个子数据集。接着继续在子数据集上选择特征，并进行数据集划分，直到创建出一个完整的决策树。创建好决策树模型后，只要根据下班后的精力和情绪情况，从根节点一路往下即可预测出下班后的行为。

问题来了，在创建决策树的过程中，要先对哪个特征进行分裂？比如上图中的例子，先判断精力指数进行分裂还是先判断情绪指数进行分裂？要回答这个问题，我们需要从信息的量化谈起。

1.信息增益

我们天天在谈论信息，那么信息要怎么样来量化呢？1948年，香农在他著名的《通信的数学原理》中提出了信息熵（Entropy）的概念，从而解决了信息的量化问题。香农认为，一条信息的信息量和它的不确定性有直接关系。一个问题不确定性越大，要搞清楚这个问题，需要了解的信息就越多，其信息熵就越大。信息熵的计算公式如下：
$$H(X)=-\sum _{x\in X}P(x)lo{g}_{2}P(x)$$
其中，P(x)表示事件x出现的概率。例如，一个盒子里分别有5个白球和5个红球，随机取出一个球。问：这个球是红色的还是白色的？这个问题的信息量多大呢？由于红球和白球出现的概率都是1/2，代入信息熵公式，可以得到其信息熵为：
$$H(X)=-(\frac{1}{2}lo{g}_2\frac{1}{2}+\frac{1}{2}lo{g}_2\frac{1}{2})=1$$
即，这个问题的信息量就是1bit。对，你没有看错，信息量的单位就是比特。我们要确定这个球是红色的还是白色的，只需要1bit的信息就够了。再举一个极端的例子，一个盒子里有10个白球，随机取出一个球，这个球是什么颜色的？这个问题的信息量是多少呢？答案是0，因为这是一个确定事件，其概率P(x)=1，代入信息熵公式，即可得到其信息熵为0。即我们不需要再获取任何新的信息，就可知道这个球一定是白色的。

回到决策树的构建问题上，当我们要构建一个决策树时，应该优先选择哪个特征来划分数据集呢？答案是：遍历所有的特征，分别计算，使用这个特征划分数据集前后信息熵的变化值，然后选择信息熵变化幅度最大的那个特征，来优先作为数据集划分依据。即选择信息增益最大的特征作为分裂节点。

比如，一个盒子里共有红、白、黑、蓝4种颜色的球共有16个，其中红球2个，白球2个，黑球4个，蓝球8个。红球和黑球的体积一样，都为1个单位；白球和蓝球的体积一样，都为2个单位。红球、白球和黑球的质量一样，都是1个单位，蓝球的质量为2个单位。

我们应该优先选择体积这个特征还是优先选择质量这个特征来作为数据集划分的依据呢？根据前面介绍的结论，我们先计算基础信息熵，即划分数据集前的信息熵。从已知信息容易知道，红球、白球、黑球、蓝球出现的概率分别为2/16，2/16，4/16，8/16，因此基础信息熵为：
$$H(D_{base})=-(\frac{2}{16}lo{g}_2(\frac{2}{16})+\frac{2}{16}lo{g}_2(\frac{2}{16})+\frac{4}{16}lo{g}_2(\frac{4}{16})+\frac{8}{16}lo{g}_2(\frac{8}{16}))=1.75$$
接着使用体积来划分数据集，此时会划分出两个数据集，第一个子数据集里是红球和黑球，第二个子数据集里是白球和蓝球，我们计算这种划分方式的信息熵。其中，第一个子数据集里，红球2个，黑球4个，其概率分别为2/6，4/6，因此第一个子数据集的信息熵为：
$$H(D{1}_{sub1}=-(\frac{2}{6}lo{g}_2(\frac{2}{6}))+\frac{4}{6}lo{g}_2(\frac{4}{6})))=0.918296$$
第二个子数据集里，白球2个，蓝球8个，其概率分别是2/10，8/10，因此第二个子数据集的信息熵为：
$$H(D{1}_{sub2})=-(\frac{2}{10}lo{g}_2(\frac{2}{10})+\frac{8}{10}lo{g}_2(\frac{8}{10}))=0.721928$$
因此，使用体积来划分数据集后，其信息熵为$H(D_1)=H(D{1}_{sub1})+H(D{1}_{sub2})=1.640224$，其信息增益为$H(D_{base})-H(D_1)=1.75-1.640224=0.109776$，如下图(a)所示：

如果我们使用质量来划分数据集，也会划分出两个子数据集，第一个子数据集里是红球、白球、黑球，第二个子数据集里只有蓝球。我们计算这种划分方式的信息熵。针对第一个子数据集，红球、白球和黑球出现的概率分别是2/8，2/8，4/8，其信息熵为：
$$H(D{2}_{sub1})=-(\frac{2}{8}lo{g}_2(\frac{2}{8})+\frac{2}{8}lo{g}_2(\frac{2}{8})+\frac{4}{8}lo{g}_2(\frac{4}{8}))=1.5$$
第二个子数据集里只有蓝球，其概率为1，因此其信息熵为$H(D{2}_{sub2})=0$。最终，我们得出使用质量划分数据集的信息熵为1.5，其信息增益为1.75-1.5=0.25，如上图(b)所示。由于使用质量划分数据集比使用体积划分数据集得到了更高的信息增益，所以我们优先选择质量这个特征来划分数据集。

下面来讨论信息增益的物理意义。我们以概率P(x)为横坐标，以信息熵Entropy为纵坐标，把信息熵和概率的函数关系$Entropy=-P(x)lo{g}_2(P(x))$，在二维坐标轴上画出来，如下图所示：

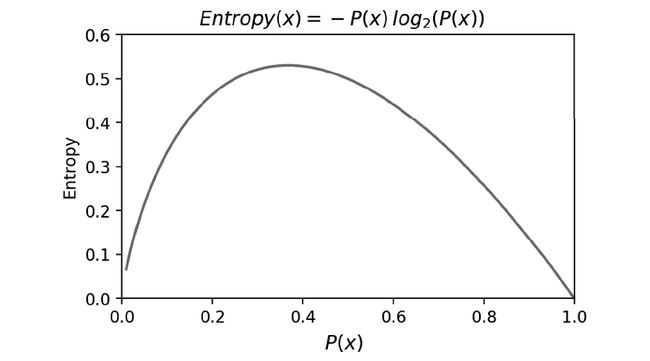
从这个函数关系可以看出来，当概率P(x)越接近0或者越接近1时，信息熵的值越小，其不确定性越小，即数据越“纯”。典型地，当概率值为1时了，此时数据是最纯净的，因此只有一种类别的数据，已经消除了不确定性，其信息熵为0。我们在特征选择时，选择信息增益最大的特征，在物理上，即让数据尽量往更纯净的方向上变换。因此，我们得出，信息增益是用来衡量数据变得更有序、更纯净的程度的指标。

熵是热力学中表征物质状态的参量之一，其物理意义是体系混乱程度的度量，被香农借用过来，作为信息量的度量。著名的信息熵增原理是这样描述的：熵增原理就是孤立热力学系统的熵不减少，总是增大或者不变。一个孤立的系统不可能朝低熵的状态发展，即不会变的有序。

用白话讲就是，如果没有外力的作用，这个世界将是越来越无序的。人活着，在于尽量让熵变低，即让世界变得更有序，降低不确定性。当我们在消费资源时，是一个增熵的过程。我们把有序的事物变成了无序的垃圾。例如我们在写书或者看书的过程，可以理解为减熵的过程。我们通过写作和阅读，减少了不确定的信息，从而实现了减熵的过程。人生价值的实现，在于消费资源（增熵过程）来获取能量，经过自己的劳动付出（减熵过程），让世界变得更加纯净有序，信息增益（减熵量 - 增熵量）即是衡量人生价值的尺度。希望我们每个人在暮年之时，回首往事，能自信地说，我给这个世界带来的信息增益是正数，且已经尽力做到最大了。

2.决策树的创建

决策树的构建过程，就是从训练数据集中归纳出一组分类规则，使它与训练数据矛盾较小的同时具有较强的泛化能力。有了信息增益来量化地选择数据集的划分特征，使决策树的创建过程变得容易了。决策树的创建基本上分为以下几个步骤：
（1）计算数据集划分前的信息熵。
（2）遍历所有未作为划分条件的特征，分别计算根据每个特征划分数据集后的信息熵。
（3）选择信息增益最大的特征，并使用这个特征作为数据划分节点来划分数据。
（4）递归地处理被划分后的所有子数据集，从未被选择的特征里继续选择最优数据划分特征来划分子数据集。

问题来了，递归过程什么时候结束呢？一般来讲，有两个终止条件：一是所有的特征都用完了，即没有新的特征可以用来进一步划分数据集。二是划分后的信息增益足够小了，这个时候就可以停止递归划分了。针对这个停止条件，需要事先选择信息增益的阈值来作为结束递归地条件。

使用信息增益作为特征选择指标的决策树构建算法，称为ID3算法。

1.离散化
如果一个特征是连续值怎么办呢？就像开头我们举过的例子，假如我们有个精力测试仪器，测出来的是一个0到100的数字，这是个连续值，这个时候怎么用决策树来建模呢？答案是：离散化。我们需要对数据进行离散化处理。例如：当精力指数小于等于40时标识为低，当大于40且小于等于70时标识为中，当大于70时标识为高。经过离散处理后，就可以用来构建决策树了。要离散化成几个类别，这个往往和具体的业务相关。

2.正则项
最大化信息增益来选择特征，在决策树的构建过程中，容易造成优先选择类别最多的特征来进行分类。举一个极端的例子，我们把某个产品的唯一标识符ID作为特征之一加入到数据集中，那么构建决策树时，就会优先选择产品ID来作为划分特征，因为这样划分出来的数据，每个叶子节点只有一个样本，划分后的子数据集最“纯净”，其信息增益最大。

这不是我们希望看到的结果。解决办法是计算划分后的子数据集的信息熵时，加上一个与类别个数成正比的正则项来作为最后的信息熵。这样当算法选择的某个类别较多的特征，使信息熵较小时，由于受到类别个数的正则项惩罚，导致最终的信息熵也比较大。这样通过合适的参数，可以使算法训练得到某种程度的平衡。
另外一个解决办法是使用信息增益比来作为特征选择的标准。具体可以参考扩展部分的内容。

3.基尼不纯度
我们知道，信息熵是衡量信息不确定性的指标，实际上也是衡量信息“纯度”的指标。除此之外，基尼不纯度（Gini impurity）也是衡量信息不纯度的指标，其计算公式是：
$$Gini(D)=\sum _{x\in X}P(x)(1-P(x))=1-\sum _{x\in X}P(x{)}^2$$
其中，$P(x)$是样本属于这个类别的概率。如果所有的样本都属于一个类别，此时$P(x)=1$，则$Gini(D)=0$，即数据不纯度最低，纯度最高。我们以概率$P(x)$作为横坐标，以这个类别的基尼不纯度$Gini(D)=P(x)(1-P(x))$作为纵坐标，在坐标轴上画出其函数关系，如图所示：

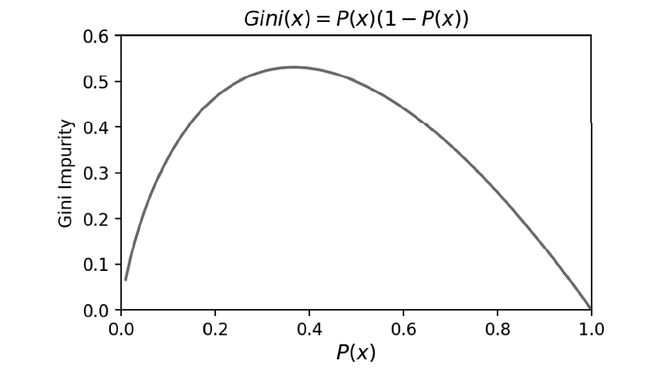
从图中可以看出，其形状和信息熵的形状几乎完全一样。CART算法使用基尼不纯度来作为特征选择标准，CART也是一种决策树构建算法。具体可以参考扩展部分的内容。

3.剪枝算法

使用决策树模型拟合数据时，容易造成过拟合。解决过拟合的方法是对决策树进行剪枝处理。决策树的剪枝有两种思路：前剪枝（Pre-Pruning）和后剪枝（Post-Pruning）。

1.前剪枝（Pre-Pruning）
前剪枝是在构造决策树的同时进行剪枝。在决策树的构建过程中，如果无法进一步降低信息熵，就会停止创建分支。为了避免过拟合，可以设定一个阈值，即使可以继续降低信息熵，也停止继续创建分支。这种方法称为前剪枝。还有一些简单的前剪枝方法，如限制叶子节点的样本个数，当样本个数小于一定的阈值时，即不再继续创建分支。

2.后剪枝（Post-Pruning）
后剪枝是指决策树构建完成之后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，信息熵的增加量是否小于某一阈值。如果小于阈值，则这一组节点可以合并成一个节点。后剪枝是目前较普遍的做法。后剪枝的过程是删除一些子树，然后用子树的根节点代替，来作为新的叶子结点。这个新的叶子节点所标识的类别通过大多数原则来确定，即把这个叶子节点里样本最多的类别，作为这个叶子节点的类别。

后剪枝算法有很多种，其中常用的一种称为降低错误率剪枝法（Reduced-Error Pruning）。其思路是，自底向上，从已经构建好的完全决策树中找出一棵子树，然后用子树的根代替这棵子树，作为新的叶子节点。叶子节点所标识的类别通过大多数原则来确定。这样就构建出了一个新的简化版的决策树。然后使用交叉验证数据集来检测这棵简化版的决策树，看其错误率是否降低了。如果错误率降低了，则可以使用这个简化版的决策树代替完全决策树。否则，还是采用原来的决策树。通过遍历所有的子树，直到针对交叉验证数据集，无法进一步降低错误率为止。

2.决策树算法参数

scikit-learn使用sklearn.tree.DecisionTreeClassifier类来实现决策树分类算法。其中几个典型的参数如下：

• criterion：特征选择算法。一种是基于信息熵，另外一种是基于基尼不纯度。研究表明，这两种算法的差异性不大，对模型准确性没有太大的影响。相对而言，信息熵运算效率会低一些，因为它有对数运算。
• splitter：创建决策树分支的选项。一种是选择最优的分支创建原则。另外一种是从排名靠前的特征中，随机选择一个特征来创建分支，这个方法和正则项的效果类似，可以避免过拟合。
• max_depth：指定决策树的最大深度。通过指定该参数，用来解决模型过拟合问题。
• min_samples_split：这个参数指定能创建分支的数据集的大小，默认是2。如果一个节点的数据样本个数小于这个数值，则不再创建分支。这就是上面介绍的前剪枝的一种方法。
• min_samples_leaf：叶子节点的最小样本数量，叶子节点的样本数量必须大于等于这个值。这也是上面介绍的另一种前剪枝的方法。
• max_leaf_nodes：最大叶子节点个数，即数据集最多能划分成几个类别。
• min_impurity_split：信息增益必须大于等于这个阈值才可以继续分支，否则不创建分支。

从这些参数可以看出，scikit-learn有一系列的参数用来控制决策树的生成过程，从而解决过拟合问题。其他参数请参阅scikit-learn的官方文档。

3.实例：预测泰坦尼克号幸存者

众所周知，泰坦尼克号是历史上最严重的一起海难事故。我们通过决策树模型，来预测哪些人可能成为幸存者。数据集下载https://www.kaggle.com/c/titanic。

数据集中总共有两个文件，都是csv格式的数据。其中，train.csv是训练数据集，包含已标注的训练样本数据。test.csv是模型进行幸存者预测的测试数据。我们的任务就是根据train.csv里的数据训练出决策树模型，然后使用该模型来预测test.csv里的数据，并查看模型的预测效果。

1.数据分析

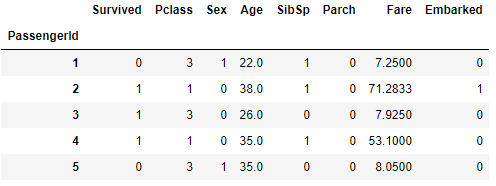
train.csv是一个892行、12列的数据表格。意味着我们有891个训练样本（扣除表头），每个样本有12个特征。我们需要先分析这些特征，以便决定哪些特征可以用来进行模型训练。

• PassengerId：乘客的ID号，这个是顺序编号，用来唯一地标识一名乘客。这个特征和幸存与否无关，丢弃这个特征。
• Survived：1表示幸存，0表示遇难。这是标注数据。
• Pclass：仓位等级。这是个很重要的特征，高仓位的乘客能更快的到达甲板，从而更容易获救。
• Name：乘客的名字，这个特征和幸存与否无关，丢弃这个特征。
• Sex：乘客性别。由于救生艇数量不够，船长让妇女和儿童先上救生艇。所以这也是个很重要的特征。
• Age：乘客的年龄。儿童会优先上救生艇，身强力壮者幸存概率也会高一些。所以这也是个很重要的特征。
• SibSp：兄弟姐妹同在船上的数量。
• Parch：同船的父辈人员的数量。
• Ticket：乘客的票号。这个特征和幸存与否无关，丢弃这个特征。
• Fare：乘客的体热指标。
• Cabin：乘客所在的船舱号。实际上这个特征和幸存与否有一定的关系，比如最早被水淹没的船舱位置，其乘客的幸存概率要低一些。但由于这个特征有大量的丢失数据，而且没有更多的数据来对船舱进行归类，因此我们丢弃这个特征的数据。
• Embarked：乘客登船的港口。我们需要把港口数据转换为数值类型的数据。

我们需要加载csv数据。并做一些预处理，包括：

• 提取Survived列的数据作为模型的标注数据。
• 丢弃不需要的特征数据。
• 对数据进行转换，以便模型处理。比如把性别数据转换为0和1.
• 处理缺失的数据。比如年龄这个特征，有很多缺失的数据。

Pandas是完成这些任务的理想软件包，我们先把数据从文件里读取出来：

import pandas as pd
def read_dataset(fname):
    # 指定第一列作为行索引
    data = pd.read_csv(fname,index_col=0)
    # 丢弃无用的数据
    data.drop(['Name','Ticket','Cabin'],axis=1,inplace=True)
    # 处理性别数据
    data['Sex'] = (data['Sex']=='male').astype('int')
    # 处理登船港口数据
    labels = data['Embarked'].unique().tolist()
    data['Embarked'] = data['Embarked'].apply(lambda n:labels.index(n))
    # 处理缺失数据
    data = data.fillna(0)
    return data

train = read_dataset('../titanic/train.csv')
train.head()

处理完的数据如下：

2.模型训练

首先需要把Survived列提取出来作为标签，并在原数据集中删除这一列。然后把数据集划分成训练数据集和交叉验证数据集。

from sklearn.model_selection import train_test_split
y = train['Survived'].values
X = train.drop(['Survived'],axis=1).values
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
print('train dataset: {0}; test dataset: {1}'.format(X_train.shape,X_test.shape))

输出如下：

train dataset: (712, 7); test dataset: (179, 7)

接着，使用scikit-learn的决策树模型对数据集进行拟合，并观察模型的性能：

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
train_score = clf.score(X_train,y_train)
test_score = clf.score(X_test,y_test)
print('train score: {0}; test score: {1}'.format(train_score,test_score))

输出如下：

train score: 0.9845505617977528; test score: 0.7877094972067039

从输出结果可以看出，针对训练样本评分很高，但是针对交叉验证数据集评分较低，两者差距较大。没错，这是过拟合现象。解决决策树过拟合的方法是剪枝，包括前剪枝和后剪枝。不幸的是scikit-learn不支持后剪枝，但是提供了一系列模型参数进行前剪枝。例如，可以通过max_depth参数限定决策树的深度，当决策树达到限定的深度时，就不再进行分裂了。这样就可以在一定程度上避免过拟合。

3.优化模型参数

我们可以选择一系列的参数值，然后分别计算指定参数训练出来的模型的评分。还可以把参数值和模型评分通过图形画出来，以便直观地发现两者之间的关系。
这里以限制决策树深度max_depth为了来介绍模型参数的优化过程。我们先创建一个函数，它使用不同的max_depth来训练模型，并计算模型评分。

# 参数选择 max_depth
def cv_score(d):
    clf = DecisionTreeClassifier(max_depth=d)
    clf.fit(X_train,y_train)
    tr_score = clf.score(X_train,y_train)
    cv_score = clf.score(X_test,y_test)
    return (tr_score,cv_score)

接着构造参数范围，在这个范围内分别计算模型评分，并找出评分最高的模型所对应的参数。

import numpy as np
depths = range(2,15)
scores = [cv_score(d) for d in depths]
tr_scores = [s[0] for s in scores]
cv_scores = [s[1] for s in scores]
best_score_index = np.argmax(cv_scores)
best_score = cv_scores[best_score_index]
best_param = depths[best_score_index]
print(scores)
print('best param: {0}； best score： {1}'.format(best_param,best_score))

输出如下：

best param: 3； best score： 0.8435754189944135

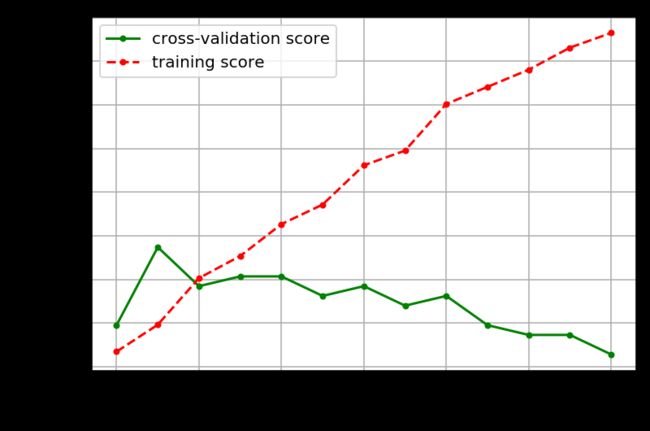
可以看到，针对模型深度这个参数，最优的值是3，其对应的交叉验证数据集评分为0.84。（你的结果可能跟我不一样，因为每次划分数据集都是随机的）我们还可以把模型参数和对应的模型评分画出来，更直观地观察其变化规律。

import matplotlib.pyplot as plt
plt.figure(figsize=(6,4),dpi=144)
plt.grid()
plt.xlabel('max depth of decision tree')
plt.ylabel('score')
plt.plot(depths,cv_scores,'.g-',label='cross-validation score')
plt.plot(depths,tr_scores,'.r--',label='training score')
plt.legend()

输出如下：

使用同样的方式，我们可以考察参数min_impurity_split。这个参数用来指定信息熵或基尼不纯度的阈值。当决策树分裂后，其信息增益低于这个阈值，则不再分裂。

# 训练模型，并计算评分
def cv_score(val):
    clf = DecisionTreeClassifier(criterion='gini', min_impurity_decrease=val)
    clf.fit(X_train, y_train)
    tr_score = clf.score(X_train, y_train)
    cv_score = clf.score(X_test, y_test)
    return (tr_score, cv_score)

# 指定参数范围，分别训练模型，并计算评分
values = np.linspace(0, 0.005, 50)
scores = [cv_score(v) for v in values]
tr_scores = [s[0] for s in scores]
cv_scores = [s[1] for s in scores]

# 找出评分最高的模型参数
best_score_index = np.argmax(cv_scores)
best_score = cv_scores[best_score_index]
best_param = values[best_score_index]
print('best param: {0}; best score: {1}'.format(best_param, best_score))

# 画出模型参数与模型评分的关系
plt.figure(figsize=(10, 6), dpi=144)
plt.grid()
plt.xlabel('threshold of entropy')
plt.ylabel('score')
plt.plot(values, cv_scores, '.g-', label='cross-validation score')
plt.plot(values, tr_scores, '.r--', label='training score')
plt.legend()

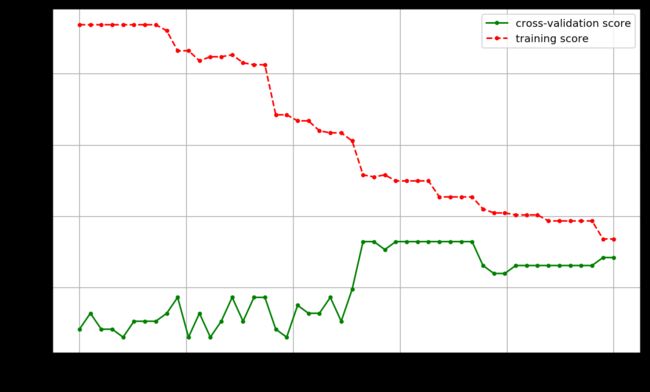
输出如下：

best param: 0.002653061224489796; best score: 0.8324022346368715

这里把[0,0.005]等分50份，以每个等分点作为信息增益阈值来训练一次模型。可以看到，训练数据集的评分急速下降，且训练评分和测试评分都保持较低水平，说明模型欠拟合。我们可以把决策树特征选择的基尼不纯度改为信息熵，即把参数criterion的值改为’entropy’观察图形的变化。

...
clf = DecisionTreeClassifier(criterion='entropy', min_impurity_decrease=val)
...

4.模型参数选择工具包

上面的模型参数优化过程存在两个问题。其一，数据不稳定，即数据集每次都是随机划分的，选择出来的最优参数在下一次运行时就不是最优的了。其二，不能一次选择多个参数，例如，想要考察max_depth和min_samples_leaf两个结合起来的最优参数就无法实现。

问题一的原因是，每次把数据集划分为训练样本和交叉验证样本时，是随机划分的，这样导致每次的训练数据集是有差异的，训练出来的模型也有差异。解决这个问题的方法是多次计算，求平均值。具体来讲，就是针对模型的某个特定的参数，多次划分数据集，多次训练模型，计算出这个参数对应的模型的最低评分、最高评分以及评价评分。问题二的解决办法比较简单，把代码再优化一下，能处理多个参数组合即可。

所幸，我们不需要从头实现这些代码。scikit-learn在sklearn.model_selection包里提供了大量模型选择和评估工具供我们使用。针对以上问题，可以使用GridSearchCV类来解决。下面先看一下使用GridSearchCV选择一个参数的最优值。

from sklearn.model_selection import GridSearchCV
thresholds = np.linspace(0,0.5,50)
param_grid = {'min_impurity_split':thresholds}
clf = GridSearchCV(DecisionTreeClassifier(),param_grid,cv=5)
clf.fit(X,y)
print("best param: {0}\nbest score: {1}".format(clf.best_params_,clf.best_score_))
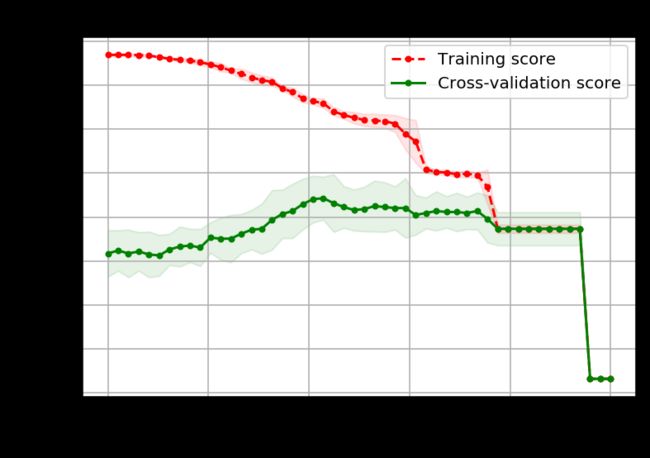
plot_curve(thresholds,clf.cv_results_,xlabel='gini thresholds')

输出如下：

best param: {'min_impurity_split': 0.21428571428571427}
best score: 0.8215488215488216

其中关键的参数是param_grid，它是一个字典，键对应的值是一个列表。GridSearchCV会枚举列表里的所有值来构建模型，最终得出指定参数值的平均评分及标准差。另外一个关键参数是cv，它用来指定交叉验证数据集的生成规则，代码中的cv=5，表示每次计算都把数据集分成5份，拿其中一份作为交叉验证数据集，其他的作为训练数据集。最终得出的最优参数及最优评分保存在clf.best_params_和clf.best_score_里。此外，clf.cv_results_保存了计算过程的所有中间结果。我们可以拿这个数据来画出模型参数与模型评分的关系图，如下所示。

def plot_curve(train_sizes,cv_results,xlabel):
    train_scores_mean = cv_results['mean_train_score']
    train_scores_std = cv_results['std_train_score']
    test_scores_mean = cv_results['mean_test_score']
    test_scores_std = cv_results['std_test_score']
    plt.figure(figsize=(6,4),dpi=144)
    plt.title('parameters turning')
    plt.grid()
    plt.xlabel(xlabel)
    plt.ylabel('score')
    plt.fill_between(train_sizes,
                     train_scores_mean-train_scores_std,
                     train_scores_mean+train_scores_std,
                     alpha=0.1,color='r')
    plt.fill_between(train_sizes,
                     test_scores_mean-test_scores_std,
                     test_scores_mean+test_scores_std,
                     alpha=0.1,color='g')
    plt.plot(train_sizes,train_scores_mean,'.--',color='r',label='Training score')
    plt.plot(train_sizes,test_scores_mean,'.-',color='g',label='Cross-validation score')
    plt.legend(loc='best')

接下来看一下如何在多组参数之间选择最优的参数组合：

from sklearn.model_selection import GridSearchCV
entropy_thresholds = np.linspace(0,1,50)
gini_thresholds = np.linspace(0,0.5,50)
param_grid = [{'criterion':['entropy'],'min_impurity_split':entropy_thresholds},
              {'criterion':['gini'],'min_impurity_split':gini_thresholds},
              {'max_depth':range(2,10)},
              {'min_samples_split':range(2,30,2)}]
clf=GridSearchCV(DecisionTreeClassifier(),param_grid,cv=5)
clf.fit(X,y)
print('best param: {0}\nbest score: {1}'.format(clf.best_params_,clf.best_score_))

输出如下：

best param: {'criterion': 'entropy', 'min_impurity_split': 0.5306122448979591}
best score: 0.8260381593714927

代码关键部分还是param_grid参数，它是一个列表，列表中的每个元素都是字典。例如：针对列表中的第一个字典，选择信息熵作为决策树特征选择的判断标准，同时其阈值范围是[0,1]之间分了50等份。GridSearchCV会针对列表中的每个字典进行迭代，最终比较列表中每个字典所对应的参数组合，选择出最优的参数。关于GridSearchCV的更多详情可参考官方文档。

最后基于好奇，使用最优参数的决策树到底是什么样呢？我们可以使用sklearn.tree.export_graphviz()函数把决策树模型导出到文件中，然后使用graphviz工具包生成决策树示意图。

from sklearn.tree import export_graphviz
clf = DecisionTreeClassifier(criterion='entropy', min_impurity_split=0.5306122448979591)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
test_score = clf.score(X_test, y_test)
print('train score: {0}; test score: {1}'.format(train_score, test_score))

columns = train.columns[1:]
# 导出 titanic.dot 文件
with open("E:/titanic.dot", 'w') as f:
    f = export_graphviz(clf, out_file=f,feature_names=columns)

# 1. conda安装 graphviz ：conda install python-graphviz 
# 2. 运行 `dot -Tpng titanic.dot -o titanic.png` 
# 3. 在当前目录查看生成的决策树 titanic.png

我们最优参数的决策树就长这个样子：

4.拓展阅读

1.熵和条件熵

在决策树创建过程中，我们会计算以某个特征创建分支后的子数据集的信息熵。用数学语言描述实际上是计算条件熵，即满足某个条件的信息熵。

关于信息熵和条件熵的相关概念，可以阅读吴军老师的《数学之美》里"信息的度量和作用"一文。《数学之美》这本书，吴军老师用平实的语言，把复杂的数学概念解释的入木三分，即使你只有高中的数学水平，也可以领略到数学的“优雅”和“威力”。

2.决策树的构建算法

本文重点介绍的决策树构建算法是ID3算法，它是1986年由Ross Quinlan提出的。1993年，该算法作者发布了新的决策树构建算法C4.5，作为ID3算法的改进，主要体现在：

• 增加了对连续值的处理，方法是使用一个阈值作为连续值的划分条件，从而把数据离散化。
• 自动处理特征值缺失问题，处理方法是直接把这个特征抛弃，不参与计算信息增益比。
• 使用信息增益比作为特征选择标准。
• 采用后剪枝算法处理过拟合，即在决策树创建完成之后，再通过合并叶子节点的方式进行剪枝。

此后，该算法作者又发布了改进的商业版本C5.0，它运算效率更高，使用内存更小，创建出来的决策树更小，并且准确性更高，适合大数据集的决策树构建。

除了前面介绍的使用基尼不纯度来构建决策树的CART算法之外，还有其他知名的决策树构建算法，如CHAID算法、MARS算法等。这里不再详述。

5.集合算法

集合算法（Ensemble）是一种元算法（Meta-algorithm），它利用统计学采样原理，训练出成百上千个不同的算法模型。当需要预测一个新样本时，使用这些模型分别对这个样本进行预测，然后采样少数服从多数的原则，决定新样本的类别。集合算法可以有效地解决过拟合问题。在scikit-learn里，所有的集合算法都实现在sklearn.ensemble包里。

1.自助聚合算法Bagging

自助聚合（Bagging，Bootstrap Aggregating的缩写）的核心思想是，采用有放回的采样规则，从m个样本的原数据集里进行n次采样（n<=m），构成一个包含n个样本的新训练数据集。重复这个过程B次，得到B个模型，当有新样本需要预测时，拿这B个模型分别对这个样本进行预测，然后采用投票方式（回归问题）得到新样本的预测值。

所谓的有放回采样规则是指，在m个数据集里，随机取出一个样本放到新数据集里，然后把这个样本放回到原数据集里，继续随机采样，直到到达采样次数n为止。由此可见，随机采样出的数据集里可能有重复数据，并且原数据集的每一个数据不一定都出现在新数据集里。

单一模型往往容易对数据噪声敏感，从而造成高方差（High Variance）。自助聚合算法可以降低对数据噪声的敏感性，从而提高模型准确性和稳定性。这种方法不需要额外的输入，只是简单地对同一个数据集训练出多个模型即可实现。当然这并不是说没有代价，自助聚合算法一般会增加模型训练的计算量。

在scikit-learn里，由BaggingClassifier类和BaggingRegressor类分别实现了分类和回归的Bagging算法。

2.正向激励算法Boosting

正向激励算法（Boosting）的基本原理是，初始化时，针对有m个训练样本的数据集，给每个样本都分配一个初始权重，然后使用这个带有权重的数据集来训练模型。训练出模型之后，针对这个模型预测错误的那些样本，增加其权重，然后拿这个更新过权重的数据集来训练出一个新的模型。重复这个过程B次，就可以训练出B个模型。
Boosting算法和Bagging算法的区别如下：

• 采样规则不同：Bagging算法是采样有放回的随机采样规则。而Boosting算法是使用增加预测错误样本权重的方法，相当于加强了对预测错误的样本的学习力度，从而提高模型的准确性。
• 训练方式不同：Bagging算法可以并行训练多个模型。而Boosting算法只能串行训练，因为下一个模型依赖上一个模型的预测结果。
• 模型权重不同：Bagging算法训练出来的B个模型的权重是一样的。而Boosting算法训练出来的B个模型本身带有权重信息，在对新样本进行预测时，每个模型的权重是不一样的。单个模型的权重由模型训练的效果来决定，即准确性高的模型权重更高。

Boosting算法有很多种实现，其中最著名的是AdaBoosting算法。在scikit-learn里由AdaBoostingClassifier类和AdaBoostingRegression类分别实现Boosting分类和Boosting回归。

3.随机森林

随机森林（RF，Random Forest）在自助聚合算法（Bagging）的基础上更进一步，对特征应用自助聚合算法。即，每次训练时，不拿所有的特征来训练，而是随机选择一个特征的子集来进行训练。随机森林算法有两个关键参数，一是构建的决策树的个数t，二是构建单棵决策树特征的个数f。

假设，针对一个有m个样本、n个特征的数据集，则其算法原理如下：
（1）单棵决策树的构建

• 采用有放回采样，从原数据集中经过m次采样，获取到一个m个样本的数据集（这个数据集里可能有重复的样本）
• 从n个特征里，采用无放回采样规则，从中取出f个特征作为输入特征。
• 重复上述过程t次，构建出t棵决策树。

（2）随机森林的分类结果
生成t棵决策树之后，对于每个新的测试样例，集合多棵决策树的预测结果来作为随机森林的预测结果。具体为，如果是回归问题，取t棵决策树的预测值的平均值作为随机森林的预测结果；如果是分类问题，采取少数服从多数的原则，取单棵决策树预测最多的那个类别作为随机森林的分类结果。

思考：为什么随机森林要选取特征的子集来构建决策树？
假如某个输入特征对预测结果是强关联的，那么如果选择全部的特征来构建决策树，这个特征都会体现在所有的决策树里面。由于这个特征和预测结果强关联，会造成所有的决策树都强烈地反映这个特征的“倾向性”，从而导致无法很好地解决过拟合问题。我们在讨论线性回归算法时，通过增加正则项来解决过拟合，它的原理就是确保每个特征都对预测结果有少量的贡献，从而避免单个特征对预测结果有过大贡献导致的过拟合问题。这里的原理是一样的。

在scikit-learn里由RandomForestClassifier类和RandomForestRegression类分别实现随机森林的分类算法和随机森林的回归算法。

4.ExtraTrees算法

ExtraTrees，叫做极限树或者极端随机树。随机森林在构建决策树的过程中，会使用信息熵或者基尼不纯度，然后选择信息增益最大的特征来进行分裂。而ExtraTrees是直接从所有特征里随机选择一个特征来分裂，从而避免了过拟合问题。

在scikit-learn里，由ExtraTreesClassifier类和ExtraTreesRegression类分别实现ExtraTrees的分类算法和ExtraTrees的回归算法。