R实现K均值算法，层次聚类算法与DBSCAN算法

1.聚类的基本概念

聚类分析(cluster analysis)仅根据在数据中发现的描述对象及其关系的信息，将数据对象分组。其目标是，组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内的相似性（同质性）越大，组间差距越大，聚类越好。即聚类分析是一组将研究对象分为相对同质的群组的统计分析技术，聚类分析也叫分类分析或数值分类。

聚类技术通常又被称为无监督学习，因为与监督学习不同，在聚类中那些表示数据类别的分类或者分组信息是没有的。

2.聚类算法

2.1基于划分的方法-K-means

2.1.1 基本思想

基于划分的方法：其原理简单来说就是，想象你有一堆散点需要聚类，想要的聚类效果就是“类内的点都足够近，类间的点都足够远”。首先你要确定这堆散点最后聚成几类，然后挑选几个点作为初始中心点，再然后依据预先定好的启发式算法给数据点做迭代重置，直到最后到达“类内的点都足够近，类间的点都足够远”的目标效果。也正是根据所谓的“启发式算法”，形成了k-means算法及其变体包括k-medoids、k-modes、k-medians。K-means算法，是以距离作为相似度的指标的算法，通过样本点到类别中心的误差平方和，作为聚类好坏的评价标准，通过不断迭代的方法使总体分类的误差平方和函数最终达到一个最小值的聚类方法。

2.1.2 基本步骤

K均值算法以K作为参数，把n个对象分成K个簇，使簇类具有较高的相似度，而簇间的相似度较低。算法处理过程如下：首先，随机地选择K个对象，每个对象初始地代表了一个簇的平均值或中心，即选择K个初始质心；对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇；然后重新计算每个簇的平均值，这个过程不断重复，直到准则函数收敛，直到质心不发生明显的变化。通常，采用平方误差准则，误差平方和SSE作为全局的目标函数，即最小化每个点到最近质心的欧几里得距离的平方和。此时，簇的质心就是该簇内所有数据点的平均值。

2.1.3 优缺点

K-means算法主要优点：

（1）是解决聚类问题的一种经典算法，简单、快速。

（2）对处理大数据集，该算法是相对可伸缩和高效率的。

（3）当结果簇是密集的，它的效果较好。

K-means算法主要缺点：

（1）在簇的中心（平均值）被定义的情况下才能使用。

（2）必须事先给出k（要生成的簇的数目），而且对初值敏感，对于不同的初始值，可能会导致不同结果。

（3）不适合于发现非凸面形状的簇或者大小差别很大的簇。

2.1.4  R软件实现算法

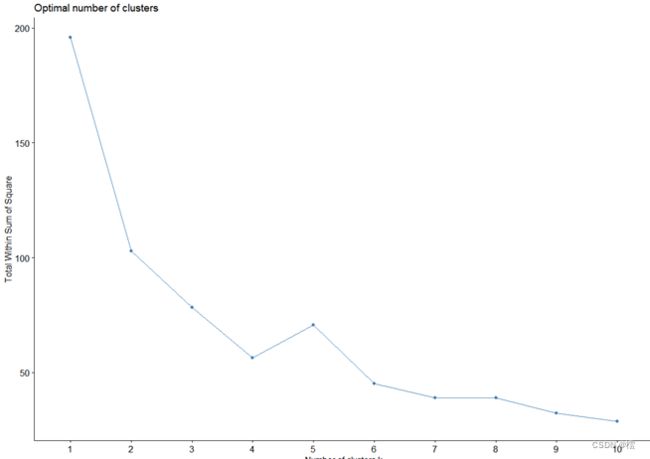
本例我们将使用R中内置的usarrest数据集，该数据集包含1973年美国每个州每10万居民因谋杀、袭击和强奸而被捕的人数，以及每个州居住在城市地区的人口百分比。首先使用 fviz_nbclust 函数创建一个图，展示聚类数量及总体平方和之间的关系，运行图如下：

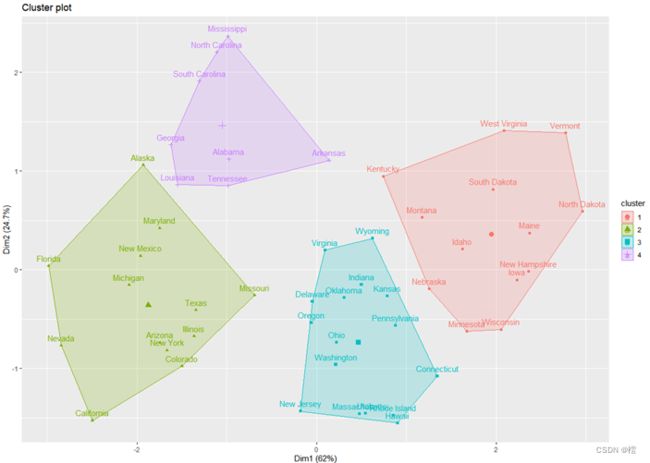
 通常我们创建这类图形寻找某个K类对应的平方和值开始弯曲或趋于平缓的肘形。上图中显然在k = 4个时出现肘形，这通常是最理想的聚类数量。因此执行kmeans函数时，使用k=4作为最优值：

 从结果可见：第一个类有16个州，第二个类有13个州，第三个类有13个州，第四个类有有8个州。

2.2 基于密度的方法-DBSCAN

2.2.1 基本思想

基于密度的方法：k-means解决不了不规则形状的聚类。于是就有了Density-based methods来系统解决这个问题。该方法同时也对噪声数据的处理比较好。其原理简单说画圈儿，其中要定义两个参数，一个是圈儿的最大半径，一个是一个圈儿里最少应容纳几个点。只要邻近区域的密度（对象或数据点的数目）超过某个阈值，就继续聚类,最后在一个圈里的，就是一个类。DBSCAN（Density-Based Spatial Clustering of Applications with Noise）就是其中的典型。

2.2.2 基本步骤

DBSCAN算法通过检查数据中每点的r邻域来搜索簇，如果点p的r邻域包含的点多于个minpts，则创建一个以p为核心对象的新簇，然后DBSCAN迭代的聚集从这些核心对象直接密度可达的对象，当没有新的点可以添加到任何簇时，该过程结束。

2.2.3 优缺点

DBSCAN的主要优点：

（1）不必指定使用它的聚类数量。需要的只是一个计算值之间距离的函数，以及一些将某些距离界定为“接近”的指令。在各种不同的分布中，DBSCAN也比K均值产生更合理的结果。

（2）密度聚类算法可以发现任何形状的样本簇，该算法具有很强的抗噪声能力

DBSCAN的主要缺点：

（1）需要用户设定合理的半径，设定对应领域内最少的样本数量MinPts

（2）当空间聚类的密度不均匀、聚类间差距很大时，聚类质量较差。

（3）当数据量增大时，要求较大的内存支持，消耗也很大。

2.2.4  R软件实现算法

采用的数据集 ：R语言factoextra包里的multishapes数据集，程序见附录例2，运行图如下所示：

2.3 基于层次的算法-层次聚类算法                                        

2.3.1 基本思想

先将n个样品各自看成一类，然后规定样品之间的“距离”和类与类之间的距离，选择距离最近的两类合并成一个新类，计算新类和其它类（各当前类）的距离，再将距离最近的两类合并，这样，每次合并减少一类，直至所有的样品都归为一类为止。

2.3.2 基本步骤

 2.3.3 优缺点

优点：

(1)距离和规则的相似度容易定义，限制少

(2)对于K-means不能解决的非球形族就可以解决了

(3)可以发现类的层次关系

(4) 有些研究表明这些算法能产生高质量的聚类，也会应用在上面说的先取K比较大的K-means后的合并阶段

缺点：

(1)计算复杂度高

(2)奇异值会对结果产生很大影响

(3)算法很可能聚类成链状

4.3.5  R软件实现算法

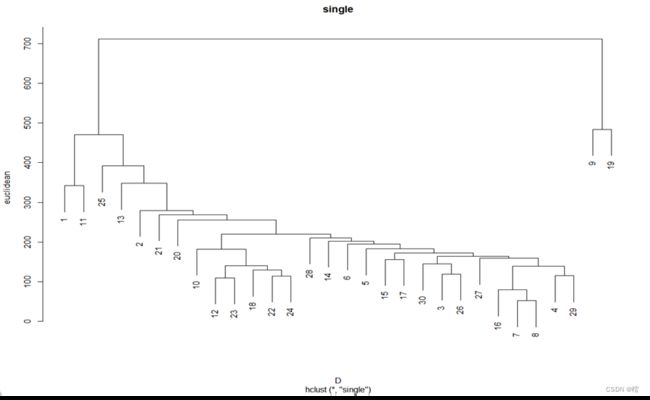
   现有反映30个省份的城镇居民家庭平均每人全年消费性支出的八个指标：食品（X1）、衣着（X2）、家庭设备用品及服务（X3）、医疗保健（X4）、交通与通信（X5）、娱乐教育文化服务（X6）、居住（X7）以及杂项商品和服务（X8），由八个指标使用层次聚类方法对30个省份进行分类，运用R软件实现结果：

 观察上图可知，城市被分为了两类，经济实力相同或地域相似的省份经常被分为一类。这符合常理。符合理论推断。

代码

#程序1
library(factoextra)
library(cluster)
df <- USArrests
df <- na.omit(df)
df <- scale(df)
head(df)
fviz_nbclust(df, kmeans, method = "wss")
gap_stat <- clusGap(df,FUN = kmeans,nstart = 25,K.max = 10,B = 50)
fviz_gap_stat(gap_stat)
# 设置随机种子，让结果可以重现
set.seed(1)
# 调用kmeans聚类算法 k = 4
km <- kmeans(df, centers = 4, nstart = 25)
# 查看结果
km
fviz_cluster(km, data = df)
#程序2
library(factoextra)
library(ggplot2)
data<-data.frame(multishapes[,1:2])
ggplot(data,aes(x,y))+geom_point()
#主函数
DBSCAN = function(data,eps,MinPts){
rows = nrow(data)
disMatrix<-as.matrix(dist(data, method = "euclidean"))#求距离
data$visited <- rep(0,rows)
names(data)<-c("x","y","visited")
data_N = data.frame(matrix(NA,nrow =rows,ncol=3))
#领域集N，存放索引、领域内的点数、点的类型
names(data_N)<-c("index","pts","cluster")
#判断点的类型，1核心点，2边界点，0噪声点
for(i in 1:rows){
if(data$visited[i] == 0){ #未被访问的点
data$visited[i] = 1  #标记已经被访问
index <- which( disMatrix[i,] <= eps)
pts <- length(index)
if(pts >= MinPts){
data_N[i,]<-c(i,pts,"1")
}else if(pts>1 && pts< MinPts){
data_N[i,]<-c(i,pts,"2")
}else{
data_N[i,]<-c(i,pts,"0") }
}
}
#删除噪声点
data_C<-data[which(data_N$cluster!=0),]
#去掉噪声点之后的领域
disMatrix2<-as.matrix(dist(data_C, method = "euclidean"))
Cluster<-list()
for(i in 1:nrow(data_C)){
Cluster[[i]]<-names(which(disMatrix2[i,]<= eps))}
#合并有交集的邻域，生成一个新簇
for(i in 1:length(Cluster)){
for(j in 1:length(Cluster)){
if(i!=j && any(Cluster[[j]] %in% Cluster[[i]])){
if(data_N[Cluster[[i]][1],]$cluster=="1"){
Cluster[[i]]<-unique(append(Cluster[[i]],Cluster[[j]]))
#合并，删除重复
Cluster[[j]]<-list() }
}
}
}
newCluster<-list() #去掉空列表
for(i in 1:length(Cluster)){
if(length(Cluster[[i]])>0){
newCluster[[length(newCluster)+1]]<-Cluster[[i]] }
}
#为相同簇中的对象赋相同的标签
data_C[,4]<-as.character()
for(i in 1:length(newCluster)){
for(j in 1:length(newCluster[[i]])){
data_C[newCluster[[i]][j],4]<-i }
}
return(data_C)
}
#运行
test<-DBSCAN(data,0.15,6)  #设定eps为0.15，minpts为6
ggplot(test,aes(x,y,colour=factor(test[,4])))+
geom_point(shape=factor(test[,4]))
#程序3
H.clust<-function(X,d="euc",m="comp",proc=FALSE,plot=TRUE)
{
D=dist(X,d)
hc <- hclust(D,m)
print(cbind(hc$merge,hc$height)) }
PROC=cbind(merge=hc$merge,height=hc$height)
if(proc) print(PROC)
if(plot) plot(hc,ylab=d,main=m)
#plot(hc,hang=hang,xlab="",ylab="",main="")
#hc1=as.dendrogram(hc)
#plot(hc1,xlab="G",ylab="D",horiz=TRUE)
#list(D=D,hc=hc,proc=proc)
return(hc)
} #C=H.clust(X)
d7.2=read.csv( "C:\\Users\\ASUS\\Desktop\\data.csv")
H.clust(d7.2,"euclidean","single",plot=T)#最短距离法