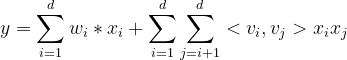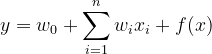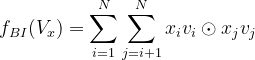推荐系统之 FNN和DeepFM和NFM
感谢FNN，让我发现自己FM，FFM还理解得不到位，于是重新跑了下别人复现的网络，感慨万千，自己怎么这么菜啊ORZ
1.FNN
我们发现，现有的网络，FM，FFM都只是做到了两路特征交叉，但发现这不够啊，表达能力不够强，于是大佬们就提出了FM与DNN交叉的FNN网络，利用神经网络对特征进行高阶的特征交叉，加强了模型对数据的学习能力。
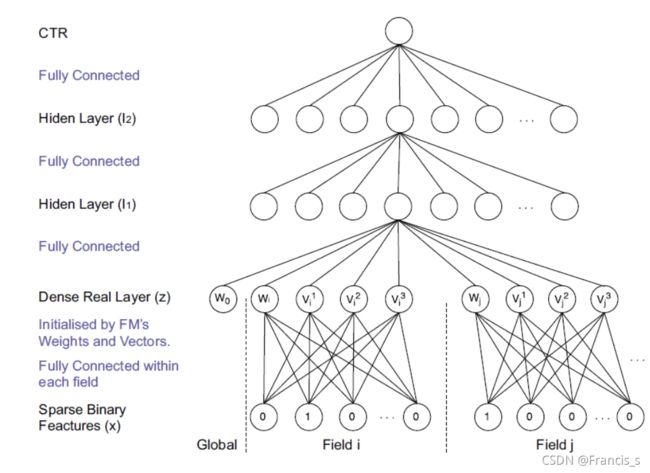
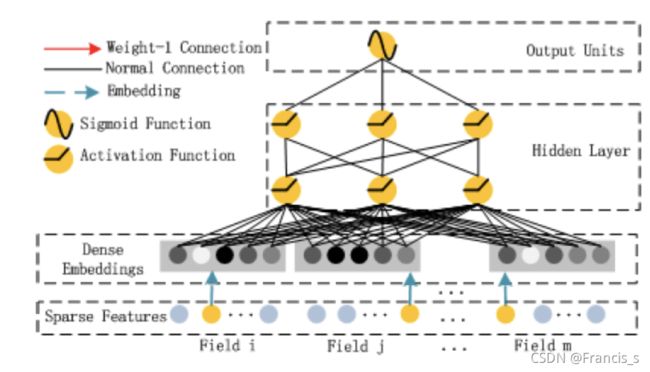
我们先来看这个网络的结构：
在神经网络的参数初始化过程中，往往采用随机出实话这种不包含任何先验信息的初始化方法，由于Embedding层的输入极端稀疏化，在随机梯度下降的过程中，只有与非零特征相连的Embedding层权重会被更新，导致Embedding层的收敛速度非常缓慢，再加上Embedding层的参数数量往往站整个网络参数数量的大半以上，因此网络的收敛速度往往取决于Embedding层的收敛速度。
针对Embedding层收敛速度慢的难题，FNN的核心在于Embedding向量的生成，FNN模型用了FM模型替换了Embedding层，在模型的正式训练之前，先提前训练好FM，然后用FM训练好的特征隐向量对正式训练的模型进行EMbedding层的初始化操作。也就是用FM作为先验提前给网络铺好路。
还有一个重点就是，在FM的训练过程中，并没有对特征域进行区分，但在FNN模型中，特征被分成了不同的特征域，因此每个特征域具有对应的Embedding层，并且每个特征域的维度都是和FM隐向量的维度保持一致的。
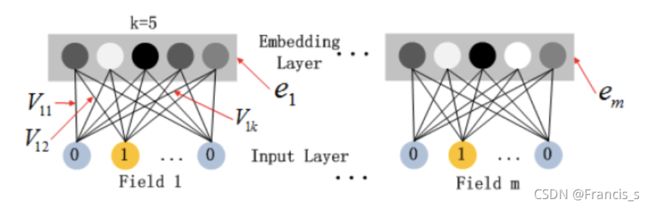
然后再来看里面的细节部分：
所以假设我们在做OneHot编码时，整个编码包含了F个特征域，然后每一个特征域的起始我们给定 ,所以我们拿到了某个特征域的Onehot编码 ![X[s_i,e_i]](http://img.e-com-net.com/image/info8/07a5e81a96d341598a02516831a051d3.gif){kind=small}
（这里的特征域指的是，一个特征对应一个特征域，不是FNN那种大类特征域的意思）
然后我们拿着这个特征域去生成一个Embedding向量，即：
所以我们整体的Embedding层输出就是：
其中，![z_i = W_0^{(i)} *x[s_i,e_i]](http://img.e-com-net.com/image/info8/ea7c7e43d1734da389df8f4810ed87b5.gif){kind=small}
，
就是映射参数，也就是所谓的Embedding映射矩阵了，而这个映射矩阵的初始化是由FM来完成的
我们来回顾一下FM的表达式：
其中，
和 
是用于表达当前特征交叉给出的隐权重向量，而
相当于第i个特征的bias（偏置）（这里一定要小心呀，我们做LR的时候是一个转换成onehot是一个单元就对应一个权重，这里就是拿单独一个权重出来，不是一个向量）
我们就取这个特征
对应的bias 以及它的隐权重向量构成一个新的向量
来组成映射参数 的第i列，所以我们可以发现 映射矩阵 的维度是 n行k+1列，n值得是特征数（Onehot后的）, K指的是隐向量的维度，+1指的是这个特征对应的bias。
然后继续求解出 稠密向量 
后，就可以继续进行后面三个全连接网络的高级特征交叉部分了。
损失函数用 交叉熵损失函数：
FNN的优势之前说了，现在来说他的缺点：
1. 只关注了高阶的特征交叉，并没有做到低阶的部分。
2. 在后面的全连接网络里面，相当于对每一种特征都做了交叉，也就是什么鬼特征都做交叉，这其实就不是那么滴合理，在POLY2那篇文章也提到过，有一些做交叉其实没什么用。
2. DeepFM
前面说了FNN没有低阶的特征交叉嘛，那我现在就来把低纬的给引入进来，于是就有了DeepFM的出现了，它集成了FM的低纬特征交叉，也集成了像DNN这样高纬的特征交叉。
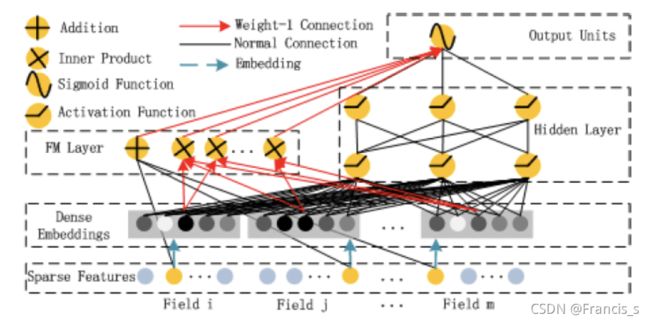
先放一个每篇博客都会放的结构图：
这尼玛就很像Wide&Deep网络结构哈哈哈，这个网络的重点就是左边的FM和右边的DNN共享相同的Embedding层的输入
左侧的FM对不同特征域的Embedding进行了两两交叉（这里的Embedding向量当成了原FM的特征隐向量）
右边的DNN对特征Embedding进行了深度交叉， 最后将FM的输出与Deep部分的输出一起送入最后的输出层，参与最后的目标拟合。
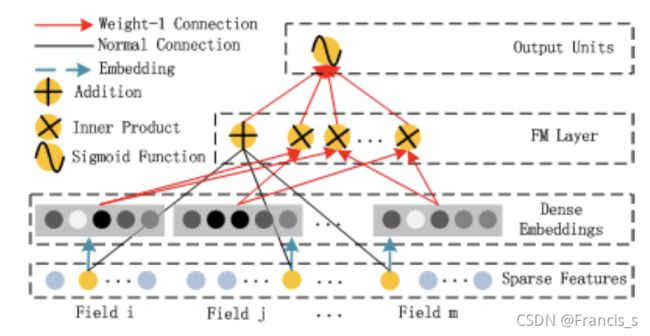
2.1 DeepFM-FM
这里面也不纯是FM，就是FM稍微改动一丢丢，有一个加法操作和一个内积操作，也就是图上的Addition和Inner Product操作。
FM这里的隐向量参数是直接和神经网络的参数一样，都是当做学习参数一块学习的，这样就省去了FM的预训练过程，而是以端到端方式训练整个网络。 且这种训练方式还有个好处，就是作者发现通过高阶和低阶交互特征一块来进行反向传播更新参数反而会使得模型表现更佳，当然，这个也依赖于共享Embedding输入的策略。
我看了下代码：假如有五个特征，每个特征都转化为onehot，然后再转Embedding，然后根据FM网络去训练出最终特征来，其实到最后如果数据是向量的话，结果就是一个数字而已。后面二阶那里别看那么求和，其实就是最后一个一个数。
2.2 DeepFM-Deep
我们一开始拿到的Embedding，就直接可以输进去网络了，如果对应隐向量是k维的话，那么输入就是一个三维的，我们假设onehot后有m个离散的向量，最后我们的输入会变成 n(特征数) * m * k
2.3 DeepFM的细节
就是在输入到Embedding这里，其实有点东西在里面的。
可以肯定的是，不通的输入特征域肯定有不同的维度，但是我们转化成embedding的维度确实一样的。
还有就是我们依然拿一开始不做处理的FM的隐权重向量来作为embedding映射矩阵的列，就是FNN那样（你看图中红色的线），但是不同的是，FNN是预训练了，咱们现在DeepFM就是把也把这个参数当作网络的一部分进行反向传播去修正 。因此，我们消除了 FM 预训练的需要，而是以端到端的方式联合训练整个网络，这样通过反向传播去修正会使模型表现更加地出色。
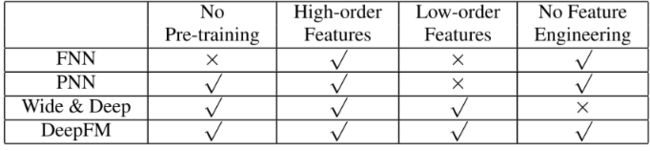
2.4 模型对比
老引用了！
FNN模型： 预训练的方式增加了开销，模型能力受限于FM表征能力的上限，且只考虑了高阶交互
PNN模型：IPNN的内积计算非常复杂， OPNN的外积近似计算损失了很多信息，结果不稳定， 且同样忽视了低阶交互
W&D模型：虽然是考虑到了低阶和高阶交互，兼顾了模型的泛化和记忆，但是Wide部分输入需要专业的特征工程经验，作者这里还举了个例子，比如用户安装应用和应用推荐中曝光应用的交叉，这个需要一些强的业务经验。
DeepFM同时考虑了上面的这些问题， 用FM换掉了W&D的LR，并Wide部分和Deep部分通过低阶和高阶特征交互来影响特征表示，从而更精确地对特征表示进行建模的策略共享了特征Embedding。
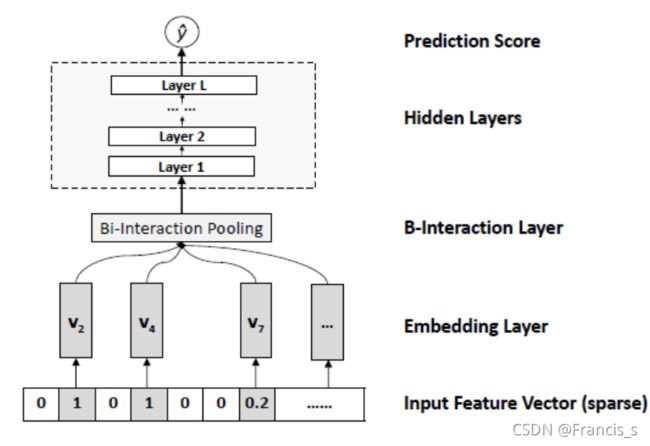
3. NFM
其实是非常类似于FM，FNN的，我们给出NFM的公式：
通过式子，其实也可以看出区别就是第三项，作者希望用一个表达力更强的函数来代替FM中二阶隐向量内积的部分。
第三项是NFM用于特征交叉的核心部分，是一个多层前馈神经网络，包含了Embedding，Bi-Interaction，Hidden 和 输出层
其中最核心的，就是Bi-Interaction这里了，因为其余的好像和PNN是一样的，下面我们先一层层地看：
3.1 Input 到 Embedding
这里还和前面稍微有点不一样。
具体的就是假如我们有x个特征，然后x个特征里面都转换成onehot编码了，所以肯定有很多0，也就是很多稀疏向量。然后我们根据FM的思想，拿到每个特征背后对应的隐向量 。最关键的一步来了
我们拿每个特征对应的onehot编码向量去乘他们自己的隐向量，这会发生什么有趣的事情呢？
输入：
输出就是 
，也就是只保留了onehot对应非0的特征向量给取下来
为啥是特征向量？还记得之前说过的话，其实这里转化为onehot之后对应的每一个维度都是也就是里面0，0，0，1，0，每一个值都是有对应的隐向量的。
这就得把所有的为1的特征向量给全取出来了。
3.2 Bi-Interaction Pooling layer
在Embedding层和神经网络之间加入了特征交叉池化层，为什么叫池化层呢？因为它是它是将一组Embedding向量转化成一个向量了：
要注意的是，这里的
不是内积，而是逐元素乘法，也就是对应元素乘对应元素。然后最后出来的还是一个向量，这就相当于FM里面的所有向量内积，然后不做最后一步，也就是不做最后的对所有隐向量求和的操作，所以当我们的隐向量有k维，这里出来的维度就是k。
3.3 Hidden Layer
就是把交叉后的特征向量走一遍全连接网络：
3.4 预测层
就是不加激活的全连接隐藏层，输出是一个单一数值
3.5 NFM的细节
在特征交叉层里面，还加入了dropout来防止过拟合地学习了高阶特征交互
还有一点不理解（没想通）：在
NFM中，为了避免特征embedding的更新改变了隐层或者预测层的输入，我们对Bi-Interaction的输出执行了BN。
Bi-Interaction池化部分来代替其他模型使用的拼接。对比于Wide&Deep模型与Deep Crossing模型完全依赖深度学习有意义的特征交互，NFM使用特征交叉池化的方式捕获了较低级别的二阶特征交互，这比拼接提供的信息更多（拼接操作的一个明显的缺点是它不考虑特征之间的任何交互。因此，这些深度学习方法必须完全依赖于后续的
deep layer来学习有意义的特征交互）。这极大地促进了NFM的后续隐藏层以更容易的方式学习有用的高阶特征交互。