详解Transformer模型及相关的数学原理

声明：本文参考了许多相关资料，视频，博客，结合《Attention is All You Need》这篇文章的每一个细节，从一个初学者的角度出发详细解读Transformer模型，无代码。原文链接及参考资料放在文末，若有错误或不当之处请指出，如有侵权请联系作者删除。

Transformer模型是谷歌在2017年提出的继卷积神经网络（CNN）模型之后新一代网络架构，最初用于自然语言处理（NLP），如今在计算机视觉领域的很多下游任务（如图像分类，目标检测，图像分割等）及其他领域也有很出色的表现，因此，理解了最基本的Transformer模型对理解以后的所有Transformer模型变种非常有帮助。

首先祭出这张经典的Transformer模型架构图（以下简称架构图），让我们一步步去理解。

宏观理解Transformer

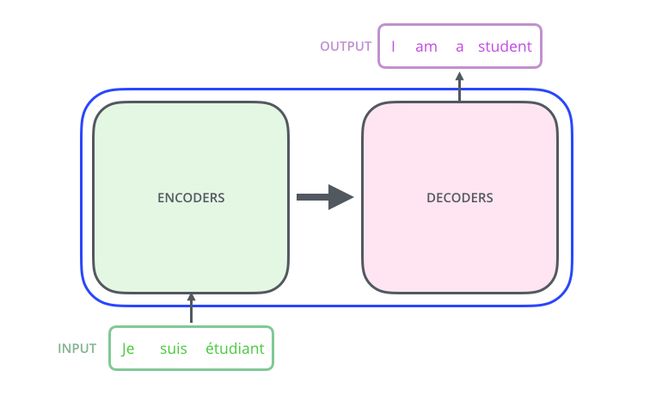
和其他所有人工智能模型一样，Transformer模型可以被当做一个黑箱（Black box）。以文本翻译中的法-英翻译任务为例，这个黑箱接受一句法语作为输入，输出一句相应的英语。
打开黑箱，我们可以发现里边由编码组件（Encoders），解码组件(Decoders) 组成，以及他们之间的连接组成。

再进一步放大看，可以发现编码组件和解码组件又由若干个相应的编码器（Encoder）和解码器（Decoder）组成。原文中这里编码器和解码器为的数目为6个（架构图中的 N× 中的 N 即为这里的个数），这个数目可以任意改变，不一定为6，只要训练出来模型的效果好就行。

要注意的是，这里所有的编码器和解码器在结构上都是相同的，但是，他们没有共享参数，也就是说每一个小的编码器和解码器的参数（或者叫权重）是独立更新的。（后续也有研究将他们中的几个进行参数共享以减少计算开销，这里不展开介绍，感兴趣的可以去搜索相关文章）。

继续放大，单独拿出一个编码器进行观察可以看到以下结构

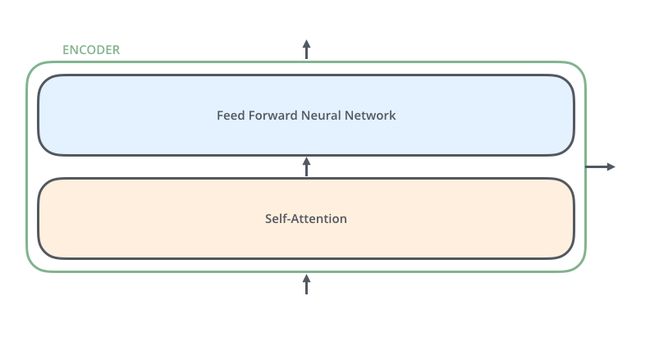
每一个编码器包含两层网络结构，自注意力层 (Self-Attention) 和 前馈神经网络层（Feed Forward Neural Network, 缩写为FFNN）。

与编码器对应，解码器在自注意力层和前馈神经网络层之间加入了一个Encoder-Decoder Attention层。

以上便是Transformer的宏观结构，下面我们将以张量的视角，从头开始查看模型细节。

Transformer结构细节

1.词编码（Word Embedding）

计算机不会直接理解我们人类的语言，在计算机中，信息的存储都是以0，1的形式进行表示的，单词，句子，图像，音乐等等都是如此。因此，我们要先将单词进行编码，用向量进行表示，通俗来说就是将单词变成计算机看得懂的语言。
词编码的手段有很多，比如独热编码（One-Hot 编码），他用以下形式进行编码，假设要编码的单词有4个（dog, apple, banana, cat）:
dog: [1, 0, 0, 0]
apple: [0, 1, 0, 1]
banana: [0, 0, 1, 0]
cat: [0, 0, 0, 1]
用这种方法进行编码方法简单，但缺点也有很多，比如：

1. 无法表达两个单词之间的相关性（距离）。
   以人类的视角来看，apple和banana，dog和cat都属于同一类的事物，apple距离banana应该比dog更近一些，但从向量上却无法反映出来。
2. 词向量维度过大，要编码的向量的维度等于单词的个数。
   单单是英语就有成千上万个单词，如果每一个单词都采用这种形式进行编码，那么所产生的向量的维度将和单词个数一致，这显然是无法接受的（上述维度是4，因为有4个单词）。
   
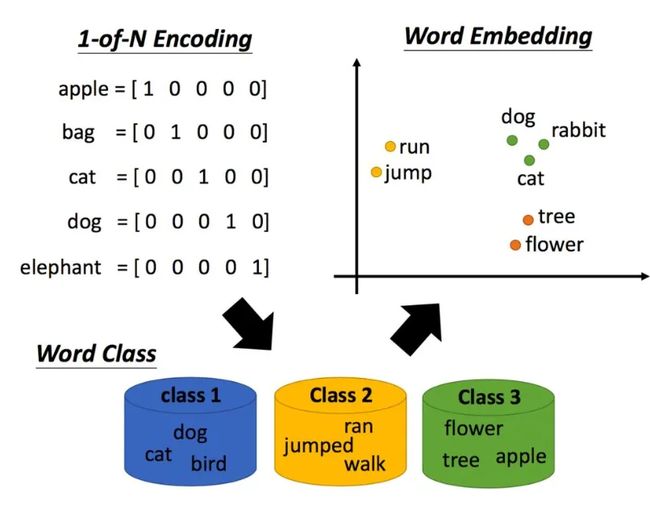
   图为Word Embedding，两个单词词义相近时，在空间也应该更近。

现在常用的编码手段依据word2vec算法对单词进行编码，具体方法参考word2vec论文。

我们将每个单词进行编码，假设Word Embedding的维度（d_model）是4（原文中是512, d_model=512），如下图所示：

现在，单词已经被我们表示成了向量，但这还不够。

2. 位置编码（Positional Encoding, 简称PE）

首先解释一下为什么Transformer需要位置编码，所谓的位置编码就是对一个句子中的每个单词贴上标签，标明他们在句子中的位置（1，2，3，4，…）。

假设我们输入一个句子不对它进行位置编码，那么 I am a student, 和 Student am a I 将被计算机认为是同一个句子，这显然不符合认知。（后续也有研究发现位置编码其实在注意力层的处理以后就消失了，这里不展开叙述。）

RNN模型中是按顺序处理一个序列，H_t 时刻的状态取决于 H_t-1 时刻，因此天生就包含了句子中的位置信息，而Transformer模型是一次处理整个句子的信息，将句子中的单词进行词编码后全部同时送入模型，因此不包含位置信息。（这也是为什么Transformer模型更擅于处理长文本序列，因为Transformer更关注全局信息，而RNN模型将模型状态储存在一个Hidden State里，因此更关注相邻几个单词之间的关系。）

那么位置编码具体是怎么操作的呢，肯定不是简单的将1，2，3，4加进去。论文中所使用的方法如下：

其中，pos是单词的位置，d_model 是位置向量的维度，和词编码的维度相等。i ∈ [0, d_model) 代表位置向量的第 i 维。根据上述公式我们可以得到第pos个位置的 d_model 向量。

下图展示了一种位置向量在第4、5、6、7维度、不同位置的的数值大小。横坐标表示位置下标，纵坐标表示数值大小。

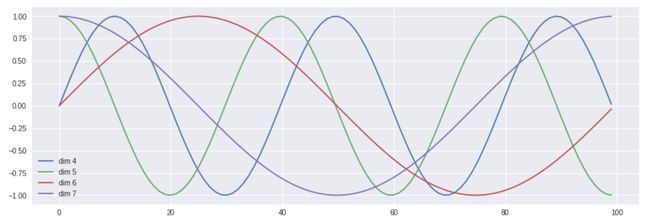
当然，上述公式不是唯一生成位置编码向量的方法。但这种方法的优点是：可以扩展到未知的序列长度。例如：当我们的模型需要翻译一个句子，而这个句子的长度大于训练集中所有句子的长度，这时，这种位置编码的方法也可以生成一样长的位置编码向量。

2.1 PE中的数学原理

为什么用三角函数，为什么偶数维（2i）用sin，奇数维（2i+1）用cos？

由三角函数性质公式：
sin(α + β) = sin α cosβ + cos α sin β
cos(α + β) = cos α cosβ - sin α sin β
将
sin(pos/10000${}^{2i/dmodel}$）= PE_(pos，2i) ，
cos(pos/10000${}^{2i/dmodel}$）= PE_(pos，2i+1),

代入上述公式有：
PE_(M+N，2i) = PE_(M，2i) × PE_(N，2i+1) + PE_(M，2i+1) × PE_(N，2i)
PE_(M+N，2i+1) = PE_(M，2i+1) × PE_(N，2i+1) - PE_(M，2i) × PE_(N，2i)

也就是说，PE_(M+N) 可由PE_(M) 与PE_(N) 相互计算得到，即各个位置间可以相互计算得到，绝对位置编码中包含了相对位置的信息。

到此，我们理解了位置编码的意义以及背后的数学规律。

3. 编码器（Encoder）

首先说明一点，除了第一个编码器外，其余编码器的输入皆为前一个编码器的输出，除了最后一个编码器外，第i个编码器的输出是第i+1个编码器的输入。

第一个编码器的输入为词编码与位置编码相加的和，所得到的新的向量可以为模型提供更多有意义的信息，比如词的位置，词之间的距离等。如下图所示：

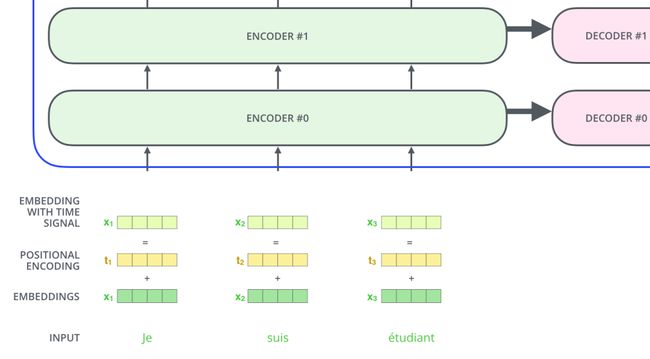
3.1 Self-Attention层

假设我们想要翻译的句子是：

The animal didn’t cross the street because it was too tired

这个句子中的 it 是一个指代词，那么 it 指的是什么呢？它是指 animal 还是street？这个问题对人来说，是很简单的，但是对模型来说并不是那么容易。但是，如果模型引入了Self Attention机制之后，便能够让模型把it和animal关联起来了。同样的，当模型处理句子中其他词时，Self Attention机制也可以使得模型不仅仅关注当前位置的词，还会关注句子中其他位置的相关的词，进而可以更好地理解当前位置的词。

上图所示的是以 “it” 这个单词为例，是当Transformer在第5层编码器编码 “it” 时的状态，可视化之后显示 “it” 有一部分注意力集中在了“The animal”上，并且把这两个词的信息融合到了 “it” 中。

3.1.1 自注意力细节

我们先看如何使用向量计算自注意力，然后再看它的矩阵实现。

注意力（attention）有加法注意力和点乘注意力，为了方便使用矩阵乘法加速运算，论文中使用的是缩放点乘注意力（Scaled Dot-Product), Scaled后边再讲。

图为Attention计算公式

先通过一个简单的例子来理解一下：什么是“self-attention自注意力机制”？

假设一句话包含两个单词：Thinking Machines。自注意力的一种理解是：Thinking-Thinking，Thinking-Machines，Machines-Thinking，Machines-Machines，共2²种两两attention。那么，具体该如何计算呢？

假设Thinking、Machines这两个单词经过词向量算法得到向量是$x_1$, $x_2$，我们将self-attention计算的6个步骤进行可视化。

1. 创建Q, K, V向量
从每个编码器的输入向量中创建三个向量，对于每个单词，创建一个查询向量（Q）、一个键向量（K）和一个值向量（V）。这些向量是通过将词嵌入向量 (X) 乘以训练过程中训练的三个矩阵（W^Q, W^K, W^V）来创建的。

注意，这些Q, K, V 向量的维度小于词嵌入向量，原文中Q, K, V向量的维度d_k = 64，而词嵌入和编码器输入/输出向量的维度d_model = 512。这是一种架构选择，可以使多头注意力（大部分）的计算保持不变。

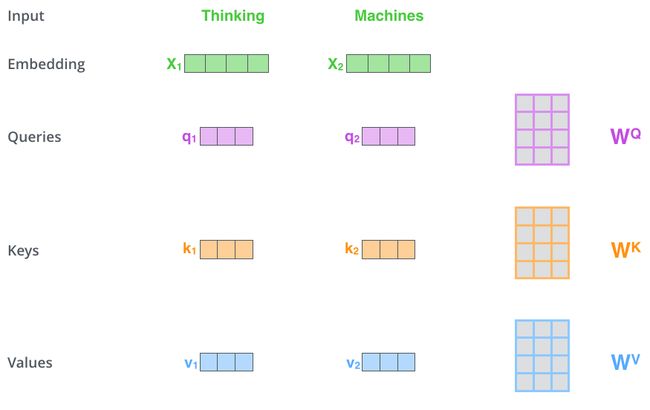
将$x_1$乘以 W^Q 权重矩阵会产生q1 ，即与该词关联的“查询”向量。我们最终为输入句子中的每个单词创建了一个“查询”、一个“键”和一个“值”投影。
2. 计算注意力分数
假设我们正在计算本例中第一个单词“Thinking”的自注意力。我们需要根据这个词对输入句子的每个词进行评分。当我们在某个位置对单词进行编码时，分数决定了对输入句子其他部分的关注程度。

分数是通过 查询向量（Q） 与我们正在评分的各个单词的 键向量（K） 的点积来计算的。因此，如果我们正在处理位置#1中单词的自注意力，第一个分数将是q1和k1的点积，第二个分数是q1和k2的点积。

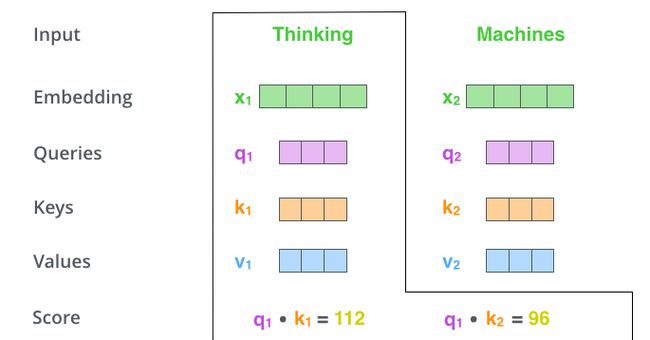
3. 缩放（Scaled）
将分数除以 8（论文中使用的 键向量（K） 维度的平方根$\sqrt{64}$ = 8。这会让梯度更稳定。这里可能还有其他可能的值，但默认是使用$\sqrt{dk}$，为什么要缩放后面会解释。
4. Softmax
将结果进行Softmax操作。Softmax 将分数归一化，因此它们都是正数并且和为 1。

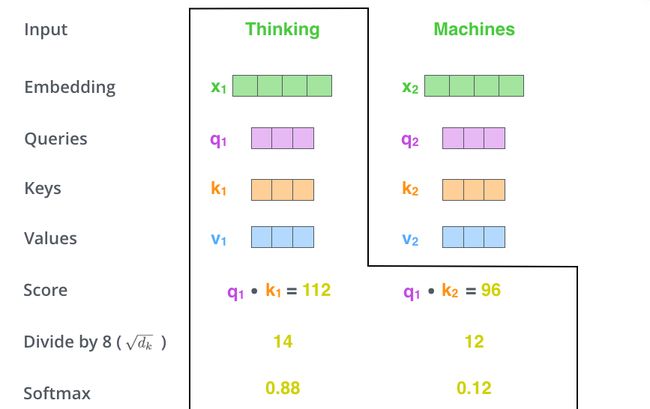
5. 乘以Value向量
在第4步进行完，得到每个词向量的分数后，将分数分别与对应的Value向量相乘。
这样做的意义在于：对于分数高的位置，相乘后的值就越大，我们把更多的注意力放到了它们身上；对于分数低的位置，相乘后的值就越小，这些位置的词可能是相关性不大的。
6. 加权求和
把第5步得到的Value向量相加，就得到了Self Attention在当前位置（这里的例子是第1个位置）对应的输出。

自注意力计算到此结束，将结果向量输入到前馈神经网络。在实际实现中，这种计算是以矩阵形式进行的，以便更快地处理。

3.1.2 自注意力的矩阵计算

首先，我们把所有词向量放到一个矩阵X中，然后分别和3个权重矩阵W^Q, W^K, W^V, 相乘，得到 Q，K，V 矩阵。矩阵X中的每一行，表示句子中的每一个词的词向量。Q，K，V 矩阵中的每一行表示 Query向量，Key向量，Value 向量，向量维度是d_k。

X 矩阵中的每一行对应于输入句子中的一个单词

第2步：由于我们使用了矩阵来计算，我们可以把上面的第 2 步到第 6 步压缩为一步，直接得到 Self Attention 的输出。

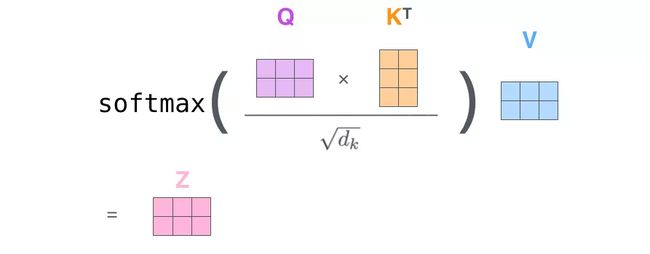
3.1.3 多头注意力机制（Multi-Head Attention）

Transformer 的论文通过增加多头注意力机制（一组注意力称为一个 attention head），进一步完善了Self-Attention。这种机制从如下两个方面增强了attention层的能力。

1. 它扩展了模型关注不同位置的能力。 在上面的例子中，第一个位置的输出​包含了句子中其他每个位置的很小一部分信息，但​仅仅是单个向量，所以可能仅由第1个位置的信息主导了。而当我们翻译句子：The animal didn’t cross the street because it was too tired时，我们不仅希望模型关注到"it"本身，还希望模型关注到"The"和“animal”，甚至关注到"tired"。这时，多头注意力机制会有帮助。
2. 多头注意力机制赋予attention层多个“子表示空间”。 下面我们会看到 ，多头注意力机制会有多组​W^Q, W^K, W^V的权重矩阵（在 Transformer 的论文中，使用了 8 组注意力),，因此可以将​变换到更多种子空间进行表示。接下来我们也使用8组注意力头（attention heads））。每一组注意力的权重矩阵都是随机初始化的，但经过训练之后，每一组注意力的权重​ 可以把输入的向量映射到一个对应的”子表示空间“。通俗来讲就是，同一件事找8个不同的人去做比只找1个人去做更好。
   

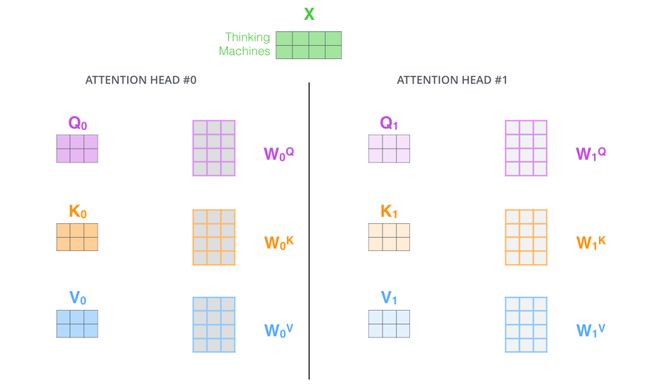
在多头注意力机制中，我们为每组注意力设定单独的​W^Q, W^K, W^V参数矩阵。将输入 X 和每组注意力的​W^Q, W^K, W^V 相乘，得到8组 Q, K, V 矩阵。

接着，我们把每组 K, Q, V 计算得到每组的 Z 矩阵，就得到8个Z矩阵。
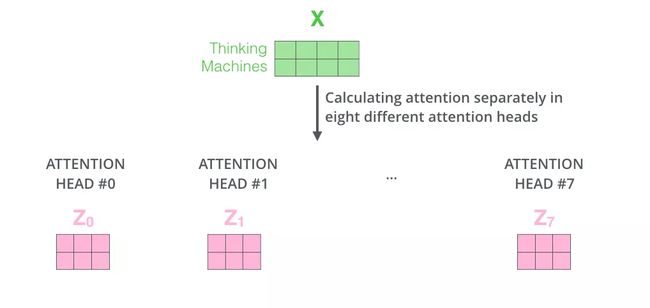由于前馈神经网络层接收的是 1 个矩阵（其中每行的向量表示一个词），而不是 8 个矩阵，所以我们直接把8个子矩阵拼接（concat）起来得到一个大的矩阵，然后和另一个权重矩阵 W^O 相乘做一次变换，映射到前馈神经网络层所需要的维度。
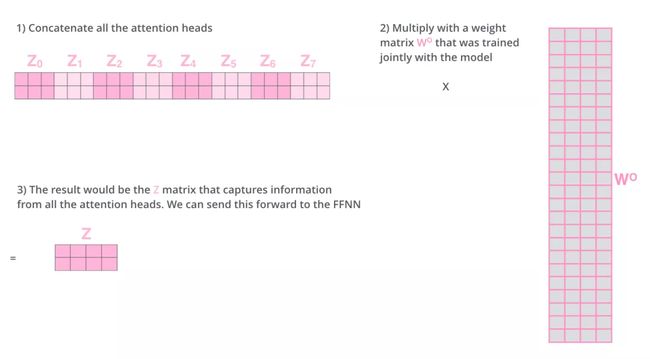总结一下就是：

1. 把8个矩阵 {Z0,Z1…,Z7} 拼接起来。
2. 把拼接后的矩阵和 W^O 权重矩阵相乘。
3. 得到最终的矩阵Z，这个矩阵包含了所有 attention heads（注意力头） 的信息。这个矩阵会输入到FFNN (Feed Forward Neural Network)层。
   以上就是多头注意力的全部内容。最后将所有内容放到一张图中：
   

再来看下前面提到的 it 的例子，不同的attention heads （注意力头）对应的“it”attention了哪些内容。下图中的绿色和橙色线条分别表示2组不同的attention heads：

当我们编码单词"it"时，其中一个 attention head （橙色注意力头）最关注的是"the animal"，另外一个绿色 attention head 关注的是"tired"。因此在某种意义上，"it"在模型中的表示，融合了 “animal” 和 “tire” 的部分表达。

3.2 残差连接和层归一化

到目前为止，我们计算得到了self-attention的输出向量。而单层encoder里后续还有两个重要的操作：残差链接、层归一化。

3.2.1 残差连接

残差连接是由何恺明等人为了缓解网络退化问题而提出（详见ResNet）。

一般认为： 网络越深，表达能力越强，性能越好。
实际现象： 在神经网络可以收敛的前提下，随着网络深度增加，网络的表现先是逐渐增加至饱和，然后迅速下降。

图为网络退化现象

残差连接本质是将网络的输出与最初的输入相加。如下图所示，将X输入网络，可将该网络看作是对X的函数F(X)，将F(X)的结果与X相加作为下一层网络的输入。

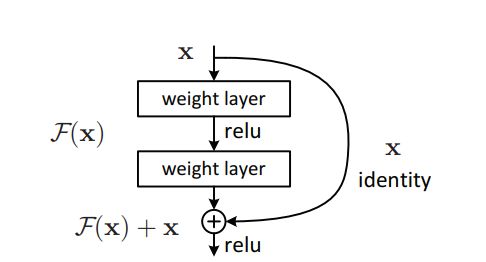
这样做可以缓解随着网络加深，模型梯度在传递过程中逐渐变得很小直至消失，导致模型参数更新缓慢的问题。

3.2.1.1为什么残差连接可以解决梯度消失？

一个残差连接，或者叫残差块（Residual block）可以表示为：
$x_{l+1}$ = H($x_l$) + F($x_l$, $W_l$)

由残差块的表示式可得：
$x_1$ = $x_0$ + F($x_0$, $W_0$)

$x_2$ = $x_1$ + F($x_1$, $W_1$) = $x_0$ + F($x_0$, $W_0$) + F($x_1$, $W_1$)

…

$x_L$ = $x_l$ +$\sum _{i=l}^{L-1}$F($x_i$, $W_i$)

上述过程说明：L层可以表示为任意一个比它浅的 $\mathbf{l}$ 层和它们之间的残差部分之和。也说明了残差网络在训练的过程中始终保留了原始信息，还增加了网络中获取的新知识。

设损失函数为Loss，则根据链式求导公式：

由损失函数的梯度计算结果可知，网络在进行反向传播时，错误信号可以不经过任何中间权重矩阵变换直接传播到低层，一定程度上可以缓解梯度消失问题（即便中间层矩阵权重很小，括号内依然有一个1，因此梯度也基本不会消失）。
残差连接使得信息前后向传播更加顺畅。

3.2.2 层归一化

编码器的每个子层（Self Attention 层和 FFNN）都有一个残差连接和层归一化（layer-normalization），如下图所示。

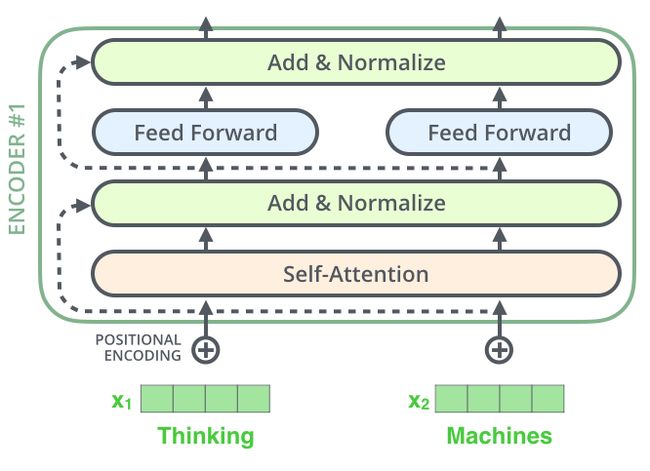
将 Self-Attention 层的层归一化（layer-normalization）和涉及的向量计算细节都进行可视化，如下所示：

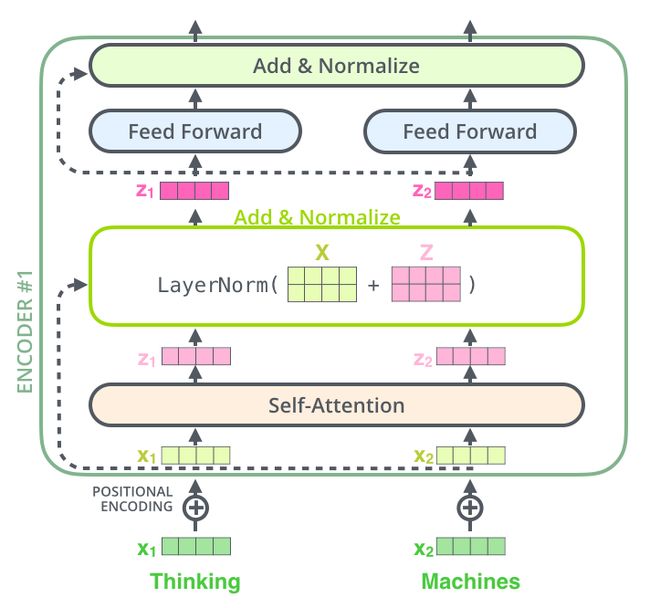
编码器和和解码器的子层里面都有层标准化（layer-normalization）。假设一个 Transformer 是由 2 层编码器和两层解码器组成的，将全部内部细节展示起来如下图所示。

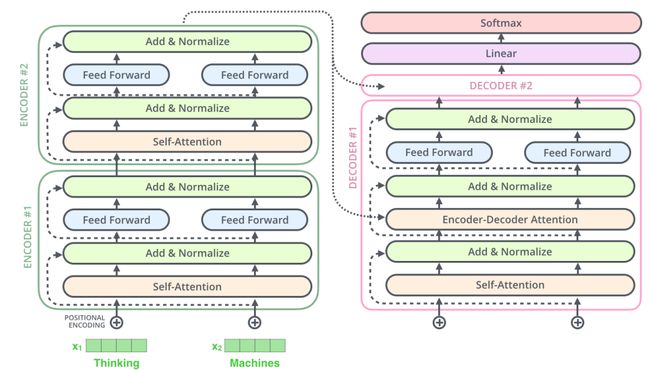
3.2.2.1 使用Normalization的目的

当我们使用梯度下降法做优化时，随着网络深度的增加，输入数据的特征分布会不断发生变化，为了保证数据特征分布的稳定性，会加入Normalization。从而可以使用更大的学习率，从而加速模型的收敛速度。同时，Normalization也有一定的抗过拟合作用，使训练过程更加平稳。

具体地，Normalization的主要作用就是把每层特征输入到激活函数之前，对它们进行normalization，使其转换为均值为1，方差为0的数据，从而可以避免数据落在激活函数的饱和区，以减少梯度消失的问题。

3.2.2.2 LayerNorm & BatchNorm

BN（BatchNorm）和LN（LayerNorm）是两种最常用的Normalization的方法，它们都是将输入特征转换为均值为1，方差为0的数据，
它们的形式是：

只不过，BN是对一个batch-size样本内的每个特征做归一化，LN是对每个样本的所有特征做归一化。以一个二维矩阵为例，它的行数代表batch_size，列数代表fea_nums。BN就是竖着进行归一化，LN则是横着进行归一化。

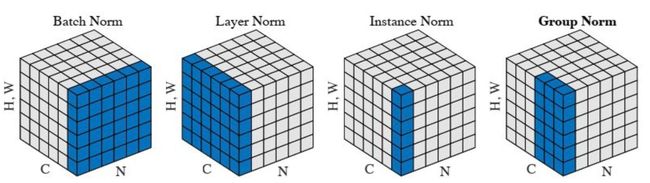
所以，BN抹平了不同特征之间的大小关系，而保留了不同样本之间的大小关系。这样，如果具体任务依赖于不同样本之间的关系，BN更有效，尤其是在CV领域，例如不同图片样本进行分类，不同样本之间的大小关系得以保留。
LN抹平了不同样本之间的大小关系，而保留了不同特征之间的大小关系。所以，LN更适合NLP领域的任务，其中，一个样本的特征实际上就是不同word embedding，通过LN可以保留特征之间的这种时序关系。

3.3 Attention中的数学原理

3.3.1 键值对注意力

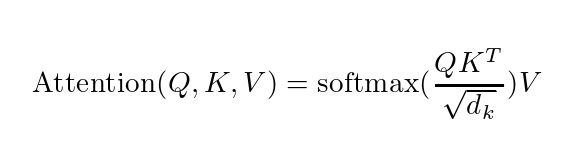
假如上面的公式很难理解，那么下面的公式读者能否知道其意义是什么呢？

Softmax(XX^T)X

我们先抛开Q K V三个矩阵不谈，self-Attention最原始的形态其实长上面这样。那么这个公式到底是什么意思呢？

我们一步一步讲

XX^T 代表什么？

一个矩阵乘以它自己的转置，会得到什么结果，有什么意义？

我们知道，矩阵可以看作由一些向量组成，一个矩阵乘以它自己转置的运算，其实可以看成这些向量分别与其他向量计算内积。（此时脑海里想起矩阵乘法的口诀，第一行乘以第一列、第一行乘以第二列…矩阵转置以后第一行不就是第一列吗？这是在计算第一个行向量与自己的内积，第一行乘以第二列是计算第一个行向量与第二个行向量的内积第一行乘以第三列是计算第一个行向量与第三个行向量的内积…）

向量的内积，其几何意义是什么？

答：表征两个向量的夹角，表征一个向量在另一个向量上的投影

记住这个知识点，我们进入一个超级详细的实例：

我们假设 X = [$x_1^T$, $x_2^T$, $x_3^T$] ,其中 X 为一个二维矩阵， $x_i^T$ 为一个行向量，对应下面的图，$x_1^T$对应"早"字embedding之后的结果，以此类推。

下面的运算模拟了一个过程，即 XX^T。我们来看看其结果究竟有什么意义。

首先，行向量 $x_i^T$ 分别与自己和其他两个行向量做内积（“早"分别与"上”"好"计算内积），得到了一个新的向量。我们回想前文提到的向量的内积表征两个向量的夹角，表征一个向量在另一个向量上的投影。那么新的向量向量有什么意义的？是行向量 $x_i^T$ 在自己和其他两个行向量上的投影。我们思考，投影的值大有什么意思？投影的值小又如何？

投影的值大，说明两个向量相关度高。

我们考虑，如果两个向量夹角是九十度，那么这两个向量线性无关，完全没有相关性！

更进一步，这个向量是词向量，是词在高维空间的数值映射。词向量之间相关度高表示什么？是不是在一定程度上（不是完全）表示，在关注词A的时候，应当给予词B更多的关注？

上图展示了一个行向量运算的结果，那么矩阵 XX^T 的意义是什么呢？

矩阵 XX^T 是一个方阵，我们以行向量的角度理解，里面保存了每个向量与自己和其他向量进行内积运算的结果。

至此，我们理解了公式 Softmax(XX^T)X 中，XX^T 的意义。我们进一步，Softmax的意义何在呢？

回想Softmax函数的公式：

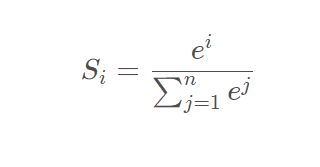
答：归一化。准确来说是，将数据映射到[0, 1]，并归一化，和为1。

我们再想，Attention机制的核心是什么？
加权求和

那么权重从何而来呢？就是这些归一化之后的数字。当我们关注"早"这个字的时候，我们应当分配0.4的注意力给它本身，剩下0.4关注"上"，0.2关注"好"。

我们仿佛已经拨开了一些迷雾，公式 Softmax(XX^T)X 已经理解了其中的一半。最后一个 X 有什么意义？完整的公式究竟表示什么？我们继续之前的计算，请看下图

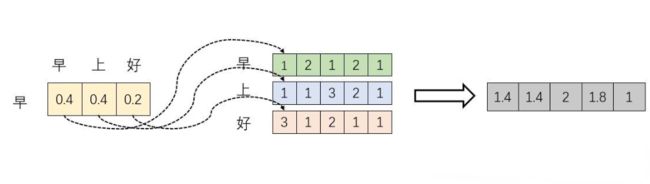
我们取 Softmax(XX^T)X 的一个行向量举例。这一行向量与 X 的一个列向量相乘，表示什么？

观察上图，行向量与 X 的第一个列向量相乘，得到了一个新的行向量，且这个行向量与 X 的维度相同。

在新的向量中，每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的，这个新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。

回想上一张可视化注意力的图中右半部分的颜色深浅，其实就是我们上图中黄色向量中数值的大小，意义就是单词之间的相关度（回想之前的内容，相关度其本质是由向量的内积度量的）。

如果您坚持阅读到这里，相信对公式Softmax(XX^T)X 已经有了更深刻的理解。

我们接下来解释原始公式中一些细枝末节的问题。

3.3.2 Q K V 矩阵

Q K V究竟是什么？我们看下面的图

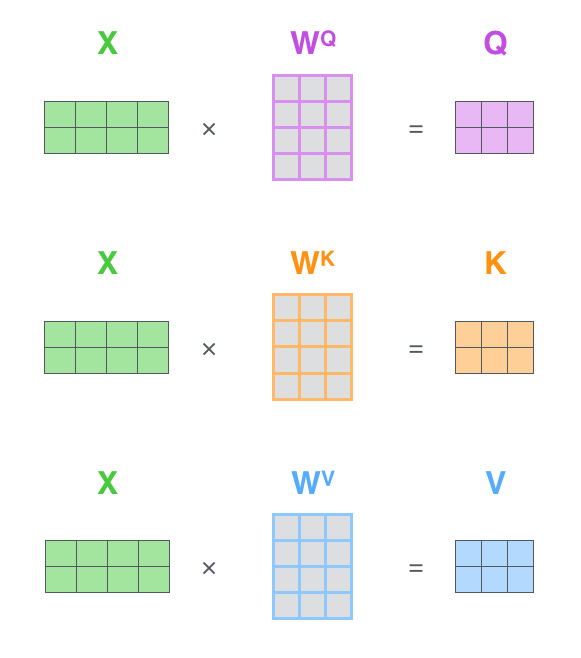
其实，所谓的Q K V矩阵、查询向量之类的字眼，其来源是 X 与矩阵的乘积，本质上都是X 的线性变换。

为什么不直接使用 X 而要对其进行线性变换？

当然是为了提升模型的拟合能力，矩阵 W 都是可以训练的，起到一个缓冲的效果。

3.3.3 $\sqrt{dk}$的意义

假设 Q, K 里的元素的均值为0，方差为1，那么A^T = Q^TK 中元素的均值为0，方差为d. 当d变得很大时，A中的元素的方差也会变得很大，如果 A 中的元素方差很大，那么 Softmax(A) 的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。

总结一下就是Softmax(A) 的分布会和 d 有关。因此A 中每一个元素除以d 后，方差又变为1。这使得Softmax(A) 的分布“陡峭”程度与d 解耦，从而使得训练过程中梯度值保持稳定。

4. 解码器（Decoder）

现在我们已经介绍了编码器中的大部分概念，我们也基本知道了编码器的原理。现在让我们来看下， 编码器和解码器是如何协同工作的。

编码器一般有多层，第一个编码器的输入是一个序列文本，最后一个编码器输出是一组序列向量，这组序列向量会作为解码器的K、V输入，其中K=V=解码器输出的序列向量表示。这些注意力向量将会输入到每个解码器的Encoder-Decoder Attention层，这有助于解码器把注意力集中到输入序列的合适位置，如下图所示。

解码阶段的每一个时间步都输出一个翻译后的单词，解码器当前时间步的输出又重新作为输入Q和编码器的输出K、V共同作为下一个时间步解码器的输入。然后重复这个过程，直到输出一个结束符。如下图所示：

解码器中的 Self Attention 层，和编码器中的 Self Attention 层的区别：

1.在解码器里，Self Attention 层只允许关注到输出序列中早于当前位置之前的单词（Masked）。
具体做法是：在 Self Attention 分数经过 Softmax 层之前，屏蔽当前位置之后的那些位置（将attention score设置成-inf）。这样做的目的是为了符合因果关系，即在解码时应当遮住未来的单词，只关注过去已经编码的单词。

2.解码器 Attention层是使用前一层的输出来构造Query 矩阵，而Key矩阵和 Value矩阵来自于编码器最终的输出。

5. 线性层和softmax

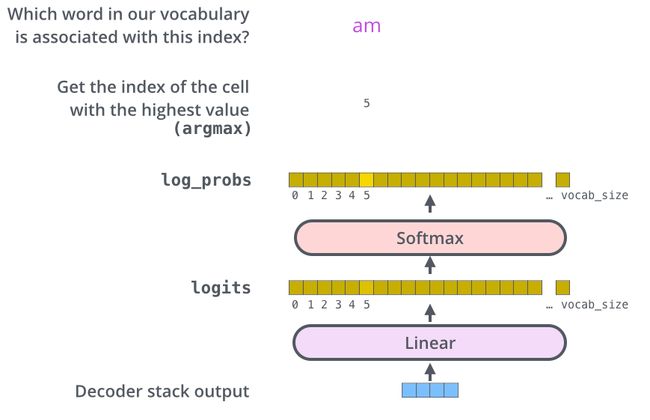
Decoder 最终的输出是一个向量，其中每个元素是浮点数。我们怎么把这个向量转换为单词呢？这是线性层和softmax完成的。

线性层就是一个普通的全连接神经网络，可以把解码器输出的向量，映射到一个更大的向量，这个向量称为 logits 向量：假设我们的模型有 10000 个英语单词（模型的输出词汇表），此 logits 向量便会有 10000 个数字，每个数表示一个单词的分数。

然后，Softmax 层会把这些分数转换为概率（把所有的分数转换为正数，并且加起来等于 1）。然后选择最高概率的那个数字对应的词，就是这个时间步的输出单词。

6. 损失函数

Transformer训练的时候，需要将解码器的输出和label一同送入损失函数，以获得loss，最终模型根据loss进行方向传播。我们用一个简单的例子来说明训练过程的loss计算：把“merci”翻译为“thanks”。

我们希望模型解码器最终输出的概率分布，会指向单词 ”thanks“（在“thanks”这个词的概率最高）。但是，一开始模型还没训练好，它输出的概率分布可能和我们希望的概率分布相差甚远，如下图所示，正确的概率分布应该是“thanks”单词的概率最大。但是，由于模型的参数都是随机初始化的，所示一开始模型预测所有词的概率几乎都是随机的。

只要Transformer解码器预测了组概率，我们就可以把这组概率和正确的输出概率做对比，然后使用反向传播来调整模型的权重，使得输出的概率分布更加接近整数输出。

那我们要怎么比较两个概率分布呢？我们可以简单的用两组概率向量的的空间距离作为loss（向量相减，然后求平方和，再开方），当然也可以使用交叉熵(cross-entropy) 和KL 散度(Kullback–Leibler divergence)。读者可以进一步检索阅读相关知识，损失函数的知识不在此展开。

由于上面仅有一个单词的例子太简单了，我们可以再看一个复杂一点的句子。句子输入是：“je suis étudiant” ，输出是：“i am a student”。这意味着，我们的transformer模型解码器要多次输出概率分布向量：

每次输出的概率分布都是一个向量，长度是 vocab_size（前面约定最大vocab size，也就是向量长度是 6，但实际中的vocab size更可能是 30000 或者 50000）
第1次输出的概率分布中，最高概率对应的单词是 “i”
第2次输出的概率分布中，最高概率对应的单词是 “am”
以此类推，直到第 5 个概率分布中，最高概率对应的单词是 “”，表示没有下一个单词了
于是我们目标的概率分布长下面这个样子：

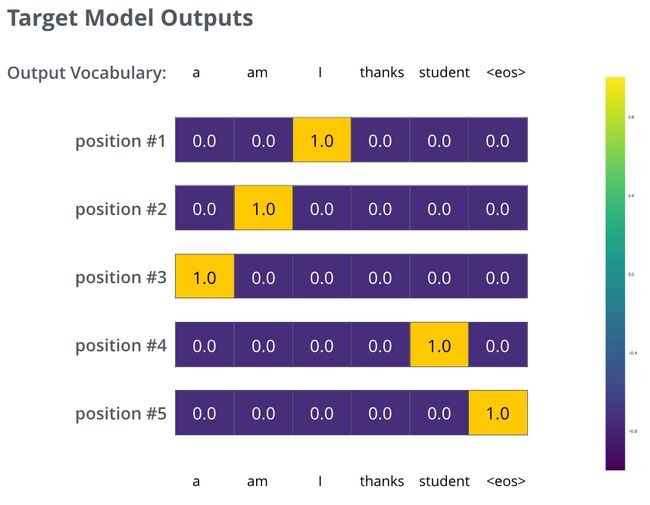
我们用例子中的句子训练模型，希望产生图中所示的概率分布 我们的模型在一个足够大的数据集上，经过足够长时间的训练后，希望输出的概率分布如下图所示：

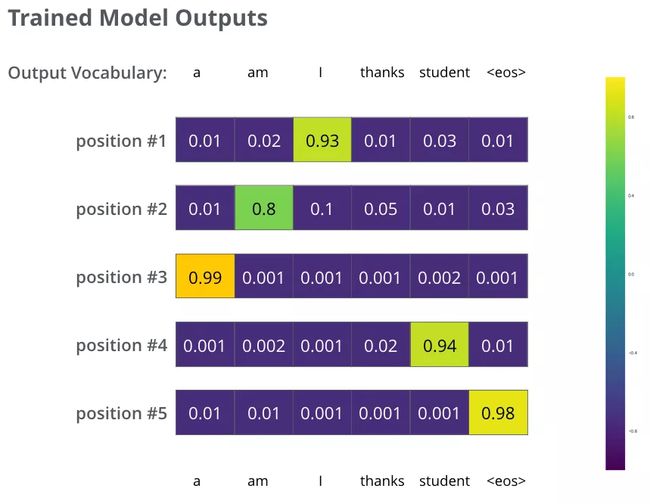
我们希望模型经过训练之后可以输出的概率分布也就对应了正确的翻译。当然，如果你要翻译的句子是训练集中的一部分，那输出的结果并不能说明什么。我们希望模型在没见过的句子上也能够准确翻译。

最后提一下greedy decoding和beam search的概念：

1. Greedy decoding：由于模型每个时间步只产生一个输出，我们这样看待：模型是从概率分布中选择概率最大的词，并且丢弃其他词。这种方法叫做贪婪解码（greedy decoding）。
2. Beam search：每个时间步保留k个最高概率的输出词，然后在下一个时间步，根据上一个时间步保留的k个词来确定当前应该保留哪k个词。假设k=2，第一个位置概率最高的两个输出的词是”I“和”a“，这两个词都保留，然后根据第一个词计算第2个位置的词的概率分布，再取出第2个位置上2个概率最高的词。对于第3个位置和第4个位置，我们也重复这个过程。这种方法称为集束搜索(beam search)。

7. 参考资料

1. Attention is All You Need
2. Deep Residual Learning for Image Recognition
3. Layer Normalization
4. http://nlp.seas.harvard.edu/annotated-transformer/
5. https://github.com/datawhalechina/learn-nlp-with-transformers
6. http://jalammar.github.io/illustrated-transformer/
7. https://zhuanlan.zhihu.com/p/410776234
8. https://www.bilibili.com/video/BV1pu411o7BE
9. https://www.bilibili.com/video/BV1cP4y1V7GF
10. https://www.bilibili.com/video/BV12L4y157MS
11. https://www.bilibili.com/video/BV1TL4y1p7M
12. https://www.bilibili.com/video/BV1MY41137AK
13. https://www.bilibili.com/video/BV1Xp4y1b7ih
14. https://blog.csdn.net/FrankieHello/article/details/122656652