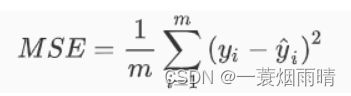机器学习西瓜书——第三章 线性模型
文章目录
-
- 线性回归
- 对数几率回归
- 线性判别分析(LDA)
- 高斯判别分析
- 多分类问题
- 类别不平衡问题
- 代码实现
-
- 线性回归
- Logistic回归
- SGDRegressor
- 局部加权线性回归
- 线性判别分析(LDA)
- 高斯判别分析
- 多项式回归
线性模型形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想,许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射而得。
由于W直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性。
线性回归
“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。
对于多变量线性回归问题

然而现实任务中该矩阵往往不是满秩矩阵。例如在许多任务中我们会遇到大量的变量,其数目甚至超过样例数,导致X的列数多于行数,该矩阵显然不满秩,此时可以解出多个最优参数W,它们都能使得均方误差最小化,选择哪一个解作为输出,将由学习算法的归纳偏好决定,常见的做法是引入正则化项。
对数几率回归
使用线性模型做分类任务,若考虑二分类任务,其输出标记y在0-1之间,可使用“单位阶跃函数”和“对数几率函数”。



线性判别分析(LDA)
严格来说LDA与Fisher判别分析稍有不同前者假设了各类样本的协方差矩阵相同且满秩。
LDA思想:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。



LDA可以从贝叶斯决策理论的角度来阐述,并可证明,当两类数据同先验、满足高斯分布且协方差相等时,LDA可达到最优分类。
若将W视为一个投影矩阵,则多分类LDA将样本投影到N-1维空间,N-1通常远小于数据原有的属性数。于是,可以通过这个投影来减少样本点的维数,且投影过程中使用了类别信息,因此LDA也被称为一种经典的监督降维技术。

高斯判别分析
多分类问题
有些二分类学习方法,例如LDA,可直接推广到多分类,但在更多情形下,我们是基于一些基本策略,利用二分类学习器来解决多分类问题。关键是如何对多分类任务进行拆分,以及如何对多个分类器进行集成,本节主要介绍拆分策略。
最经典的拆分策略有三种:“一对一OvO”,“一对其余OvR”和“多对多MvM”。
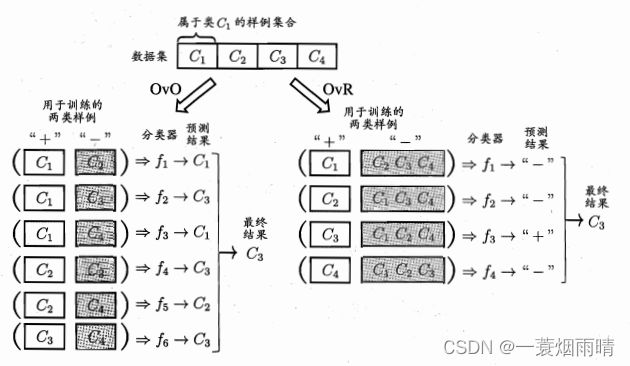
OvR只需训练N个分类器,而OvO需训练N(N-1)/2个分类器,在类别很多时,OvO的训练时间开销通常比OvR更小。
MvM是每次将若干类作为正类,若干其他类作为反类。MvM的正、反类构造必须有特殊的设计,不能随意选取。常用的MvM技术:“纠错输出码(ECOC)”
ECOC是将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性,主要分为两步:
- 编码:对N个类别做M次划分,每次划分将一部分划为正类,一部分划为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可以训练出M个分类器。
- 解码:M个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其距离最小的类别作为最终预测结果。
类别划分通过“编码矩阵”指定,编码矩阵有多种形式,常见的主要有二元码和三元码,前者将每个类别分别指定为正类和反类,后者在正、反类之外,还可指定“停用类”。
类别不平衡问题
前面介绍的分类学习方法都有一个共同的基本假设,即不同类别的训练样例数目相当。
例如有998个反例,但正例只有2个,那么学习方法只需返回一个永远将新样本预测为反例的学习器,就能达到99.8%的精度;然而这样的学习器往往没有价值,因为它不能预测出任何正例。

再缩放的思想虽简单,但实际操作却并不平凡,主要因为“训练集是真实样本总体的无偏采样”这个假设往往并不成立,也就是说,我们未必能有效地基于训练集观测几率来推断出真实几率。是“代价敏感学习”的基础,代价敏感学习研究非均等代价下的学习。
现有技术大体上有三类做法:
- “欠采样”,即去除一些反例使得正、反例数目接近,然后进行学习;
- “过采样”,即增加一些正例使得正、反例数目接近,然后进行再学习;
- “阈值移动”,直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将(3.48)嵌入到其决策过程中。
过采样法不能简单地对初试正例样本进行重复采样,否则会招致严重的过拟合;过采样法的代表性算法SMOTE是通过对训练集里的正例进行插值来产生额外的正例。
欠采样法若随机丢弃反例,可能丢失一些重要信息,代表算法是EasyEnsemble则是利用集成学习机制,将反例划分为若干个集合供不同学习器使用,这样对每个学习器来看都进行了欠采样,但全局来看却不会丢失重要信息。
代码实现
线性回归
参考 numpy,linear_model.LinearRegression()和linear_model.Ridge(alpha=0., solver='lsqr')三种实现方式。
import numpy as np
from sklearn import linear_model
class LinearRegression:
def __init__(self):
self.w=None
self.n_features=None
def fit(self,X,y):
"""
w=(X^TX)^{-1}X^Ty
"""
assert isinstance(X,np.ndarray) and isinstance(y,np.ndarray)
assert X.ndim==2 and y.ndim==1
assert y.shape[0]==X.shape[0]
n_samples = X.shape[0]
self.n_features=X.shape[1]
extra=np.ones((n_samples,))
X=np.c_[X,extra]
if self.n_features<n_samples:
self.w=np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
else:
raise ValueError('dont have enough samples')
def predict(self,X):
n_samples=X.shape[0]
extra = np.ones((n_samples,))
X = np.c_[X, extra]
if self.w is None:
raise RuntimeError('cant predict before fit')
y_=X.dot(self.w)
return y_
if __name__=='__main__':
X=np.array([[1.0,0.5,0.5],[1.0,1.0,0.3],[-0.1,1.2,0.5],[1.5,2.4,3.2],[1.3,0.2,1.4]])
y=np.array([1,0.5,1.5,2,-0.3])
lr=LinearRegression()
lr.fit(X,y)
X_test=np.array([[1.3,1,3.2],[-1.2,1.2,0.8]])
y_pre=lr.predict(X_test)
print(y_pre)
sklearn_lr=linear_model.LinearRegression()
sklearn_lr.fit(X,y)
sklearn_y_pre=sklearn_lr.predict(X_test)
print(sklearn_y_pre)
ridge_reg = linear_model.Ridge(alpha=0., solver='lsqr') # 可选择具有l2正则化
ridge_reg.fit(X, y)
ridge_y_pre=ridge_reg.predict(X_test)
print(ridge_y_pre)
所算结果一致:
[0.72595294 2.05195332]
[0.72595294 2.05195332]
[0.72595294 2.05195332]
参考对以上建立的模型求指标:
# 截距项
lr.w[-1]
sklearn_lr.intercept_
ridge_reg.intercept_
0.38361347550256863
0.38361347550256863
0.38361347550256775
# 回归系数(斜率)
lr.w[:-1]
sklearn_lr.coef_
ridge_reg.coef_
array([-0.45948582, 0.92846221, 0.00350276])
array([-0.45948582, 0.92846221, 0.00350276])
array([-0.45948582, 0.92846221, 0.00350276])
# 均方误差,拟合数据和原始数据对应样本点的误差的平方和的均值
((y-sklearn_lr.predict(X))**2).sum()/ X.shape[0]
from sklearn.metrics import mean_squared_error
mean_squared_error(y,sklearn_lr.predict(X))
from sklearn.metrics import mean_squared_error
mean_squared_error(y,ridge_reg.predict(X))
0.11602502065506759
0.11602502065506759
0.11602502065506762

即1−我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例 ,越接近1越好。
1-(((y-sklearn_lr.predict(X))**2).sum())/(((y - y.mean())**2).sum())
from sklearn.metrics import r2_score
r2_score(y,sklearn_lr.predict(X))
sklearn_lr.score(X,y)
0.8171106231792755
0.8171106231792755
0.8171106231792755
sklearn下载糖尿病数据集,抽取一列属性,用于做一元线性回归。
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
#加载糖尿病数据集
diabetes = datasets.load_diabetes()
X = diabetes.data[:,np.newaxis ,2] #diabetes.data[:,2].reshape(diabetes.data[:,2].size,1)
y = diabetes.target
X_train , X_test , y_train ,y_test = train_test_split(X,y,test_size=0.2,random_state=42)
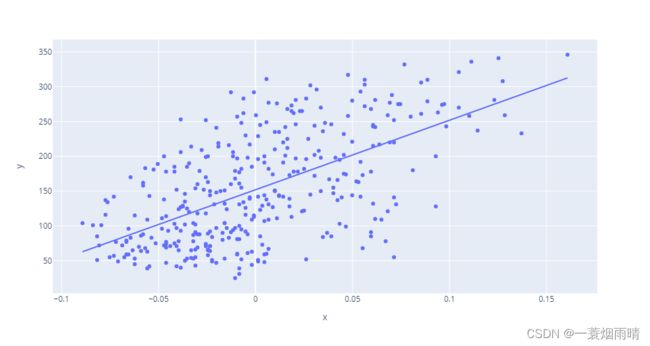
# plotly回归线与点图
import plotly.express as px
fig=px.scatter(x=X_train.reshape(X_train.shape[0],), y=y_train,trendline="ols")
fig.show()
from sklearn import linear_model
sklearn_lr=linear_model.LinearRegression()
sklearn_lr.fit(X_train,y_train)
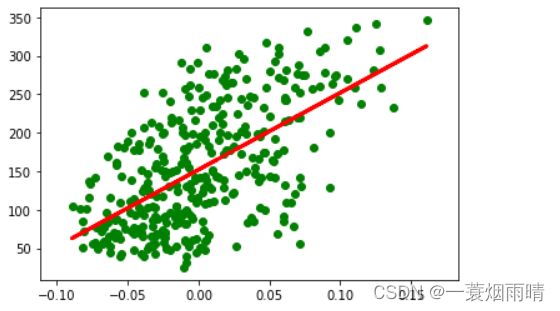
from matplotlib import pyplot as plt
plt.scatter(X_train , y_train ,color ='green')
plt.plot(X_train ,sklearn_lr.predict(X_train) ,color='red',linewidth =3)
plt.show()
一元线性回归R语言实现参见博客
Logistic回归
参考
numpy牛顿法、torch随机梯度下降和sklearn库实现。
以下是输入数据格式:
import numpy as np
from sklearn import linear_model
from sklearn.datasets import load_breast_cancer # 乳腺癌数据集
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
np.random.seed(42)
import torch
from torch import nn,optim
class SGDLogisticRegression: # 随机梯度下降
class LogisticRegressionModel(nn.Module): # nn.Module作为LogisticRegressionModel的父类
def __init__(self,n_features):
super(SGDLogisticRegression.LogisticRegressionModel,self).__init__() # 是对继承自父类的属性进行初始化
self.linear=nn.Linear(n_features,1) # 全连接层,即线性函数部分
self.sigmoid=nn.Sigmoid() # Sigmoid()函数层
def forward(self,X):
return self.sigmoid(self.linear(X))
def __init__(self,max_iter=100000,learning_rate=0.005):
self.max_iter=max_iter # 最大迭代次数
self.learning_rate=learning_rate # 学习率
self.criterion=nn.BCELoss() # 二分类的交叉熵
# self.fitted=False # 不知道是做什么用
def fit(self,X,y):
n_feature=X.shape[1] # 几个变量(属性)
self.model=SGDLogisticRegression.LogisticRegressionModel(n_feature) # 模型
self.optimizer=optim.SGD(self.model.parameters(),lr=self.learning_rate) # SGD优化器
X=torch.from_numpy(X.astype(np.float32))
y=torch.from_numpy(y.astype(np.float32))
for epoch in range(self.max_iter):
y_predict=self.model(X)[:,0]
loss=self.criterion(y_predict,y)
# print('epoch:',epoch,' loss.item():',loss.item())
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
def predict(self,X):
X = torch.from_numpy(X.astype(np.float32))
with torch.no_grad():
y_pred = self.model(X).detach().numpy() # tensor.detach()返回一个新的tensor,从当前计算图中分离下来的,但是仍指向原变量的存放位置,不同之处只是requires_grad为false,得到的这个tensor永远不需要计算其梯度,不具有grad。
y_pred[y_pred>0.5]=1
y_pred[y_pred<=0.5]=0
return y_pred[:,0]
def predict_proba(self,X):
X = torch.from_numpy(X.astype(np.float32))
with torch.no_grad():
y_pred = self.model(X).detach().numpy() # tensor.detach()返回一个新的tensor,从当前计算图中分离下来的,但是仍指向原变量的存放位置,不同之处只是requires_grad为false,得到的这个tensor永远不需要计算其梯度,不具有grad。
y_pred = np.c_[y_pred, 1-y_pred]
return y_pred
class LogisticRegression:
def __init__(self,max_iter=100,use_matrix=True):
self.beta=None # 线性函数部分参数向量
self.n_features=None #
self.max_iter=max_iter # 最大迭代次数
self.use_Hessian=use_matrix
def fit(self,X,y):
n_samples=X.shape[0] # 数据量
self.n_features=X.shape[1] # 属性量
extra=np.ones((n_samples,))
X=np.c_[X,extra] # np.c_是按行连接两个矩阵,就是把两矩阵左右相加
self.beta=np.random.random((X.shape[1],)) # 线性函数部分参数向量
for i in range(self.max_iter):
if self.use_Hessian is not True: # 如果不使用黑塞矩阵(Hessian Matrix
dldbeta=self._dldbeta(X,y,self.beta)
dldldbetadbeta=self._dldldbetadbeta(X,self.beta)
self.beta-=(1./dldldbetadbeta*dldbeta)
else:
dldbeta = self._dldbeta(X, y, self.beta)
dldldbetadbeta = self._dldldbetadbeta_matrix(X, self.beta)
self.beta -= (np.linalg.inv(dldldbetadbeta).dot(dldbeta))
@staticmethod
def _dldbeta(X,y,beta):
# 《机器学习》 公式 3.30
m=X.shape[0]
sum=np.zeros(X.shape[1],).T
for i in range(m):
sum+=X[i]*(y[i]-np.exp(X[i].dot(beta))/(1+np.exp(X[i].dot(beta))))
return -sum
@staticmethod # 静态方法
def _dldldbetadbeta_matrix(X,beta):
m=X.shape[0]
Hessian=np.zeros((X.shape[1],X.shape[1]))
for i in range(m):
p1 = np.exp(X[i].dot(beta)) / (1 + np.exp(X[i].dot(beta)))
tmp=X[i].reshape((-1,1))
Hessian+=tmp.dot(tmp.T)*p1*(1-p1)
return Hessian
@staticmethod
def _dldldbetadbeta(X,beta):
# 《机器学习》公式 3.31
m=X.shape[0]
sum=0.
for i in range(m):
p1=np.exp(X[i].dot(beta))/(1+np.exp(X[i].dot(beta)))
sum+=X[i].dot(X[i].T)*p1*(1-p1)
return sum
def predict_proba(self,X):
n_samples = X.shape[0]
extra = np.ones((n_samples,))
X = np.c_[X, extra]
if self.beta is None:
raise RuntimeError('cant predict before fit')
p1 = np.exp(X.dot(self.beta)) / (1 + np.exp(X.dot(self.beta)))
p0 = 1 - p1
return np.c_[p0,p1]
def predict(self,X):
p=self.predict_proba(X)
res=np.argmax(p,axis=1)
return res
if __name__=='__main__':
breast_data = load_breast_cancer() # 乳腺癌数据集
X, y = breast_data.data[:,:7], breast_data.target # 只选择了前7个属性
X = MinMaxScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
tinyml_logisticreg = LogisticRegression(max_iter=100,use_matrix=True)
tinyml_logisticreg.fit(X_train, y_train)
lda_prob = tinyml_logisticreg.predict_proba(X_test)
lda_pred = tinyml_logisticreg.predict(X_test)
# print('tinyml logistic_prob:', lda_prob)
# print('tinyml logistic_pred:', lda_pred)
print('tinyml accuracy:', len(y_test[y_test == lda_pred]) * 1. / len(y_test))
sklearn_logsticreg = linear_model.LogisticRegression(max_iter=100,solver='newton-cg')
sklearn_logsticreg.fit(X_train, y_train)
sklearn_prob = sklearn_logsticreg.predict_proba(X_test)
sklearn_pred = sklearn_logsticreg.predict(X_test)
# print('sklearn prob:',sklearn_prob)
# print('sklearn pred:',sklearn_pred)
print('sklearn accuracy:', len(y_test[y_test == sklearn_pred]) * 1. / len(y_test))
torch_sgd_logisticreg=SGDLogisticRegression(100000,0.01)
torch_sgd_logisticreg.fit(X_train,y_train)
torch_pred=torch_sgd_logisticreg.predict(X_test)
torch_prob=torch_sgd_logisticreg.predict_proba(X_test)
#print('torch prob:', torch_prob)
print('torch accuracy:',len(y_test[y_test==torch_pred])/len(y_test))
# expected output
"""
tinyml accuracy: 0.9590643274853801
sklearn accuracy: 0.9298245614035088
torch accuracy: 0.9532163742690059
"""
SGDRegressor
参考 SGD线性回归numpy(L1,L2,L1+L2)和sklearn库实现.
import numpy as np
from sklearn import linear_model
# 采用MSE作为损失函数
# penalty = 'l2' 则为 Ridge Regression 岭回归
# penalty = 'l1' 则为 Lasso Regression
# penalty = 'l1l2' 则为 Elastic Net
# alpha 为 正则化系数
np.random.seed(1)
class SGDRegressor:
def __init__(self,max_iter=100,penalty=None,alpha=1e-3,l1_ratio=0.5):
self.w = None
self.n_features = None
self.penalty=penalty
self.alpha=alpha
self.l1_ratio=l1_ratio
self.max_iter=max_iter
#
def fit(self, X, y):
assert isinstance(X, np.ndarray) and isinstance(y, np.ndarray)
assert y.shape[0] == X.shape[0]
n_samples = X.shape[0]
self.n_features = X.shape[1]
extra = np.ones((n_samples,1))
X = np.c_[X,extra]
self.w=np.random.randn(X.shape[1],1)
for iter in range(self.max_iter):
for i in range(n_samples):
sample_index=np.random.randint(n_samples)
x_sample=X[sample_index:sample_index+1]
y_sample=y[sample_index:sample_index+1]
lr=SGDRegressor.learning_schedule(iter*n_samples+i)
# 求导
grad=2*x_sample.T.dot(x_sample.dot(self.w)-y_sample)
if self.penalty is not None:
# Ridge
if self.penalty=='l2':
grad+=self.alpha*self.w
# Lasso
elif self.penalty=='l1':
grad+=self.alpha*np.sign(self.w)
# Elastic Net
elif self.penalty=='l1l2':
grad+=(self.alpha*self.l1_ratio*np.sign(self.w)+
(1-self.l1_ratio)*self.alpha*self.w)
self.w=self.w-lr*grad
def predict(self, X):
n_samples = X.shape[0]
extra = np.ones((n_samples,1))
X = np.c_[X,extra]
if self.w is None:
raise RuntimeError('cant predict before fit')
y_ = X.dot(self.w)
return y_
@staticmethod
def learning_schedule(t):
return 5 / (t + 50)
if __name__ == '__main__':
# X = np.random.rand(100,3)
# y = np.random.rand(100,3).dot(np.ones((3,1)))
# y=y.ravel() # ravel() 函数将数组多维度拉成一维数组
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
#加载糖尿病数据集
diabetes = datasets.load_diabetes()
X = diabetes.data[:,np.newaxis ,2] #diabetes.data[:,2].reshape(diabetes.data[:,2].size,1)
y = diabetes.target
X , _ , y ,_ = train_test_split(X,y,test_size=0.2,random_state=42)
print(X.shape)
print(y.shape)
lr = SGDRegressor(max_iter=20000,penalty='l1',alpha=1e-3,l1_ratio=0.5)
lr.fit(X, y)
print('w:',lr.w)
sklearn_lr = linear_model.SGDRegressor(max_iter=20000,penalty='l1',alpha=1e-3)
sklearn_lr.fit(X, y)
print(sklearn_lr.coef_)
print(sklearn_lr.intercept_)
局部加权线性回归
参见1 参见2
import numpy as np
import matplotlib.pyplot as plt
class LocallyWeightedLinearRegression:
def __init__(self,tau):
self.tau=tau
self.w=None
def fit_predict(self,X,y,checkpoint_x):
m = X.shape[0]
self.n_features = X.shape[1]
extra = np.ones((m,))
X = np.c_[X, extra]
checkpoint_x=np.r_[checkpoint_x,1]
self.X=X
self.y=y
self.checkpoint_x=checkpoint_x
weight=np.zeros((m,))
for i in range(m):
weight[i]=np.exp(-(X[i]-checkpoint_x).dot((X[i]-checkpoint_x).T)/(2*(self.tau**2)))
weight_matrix=np.diag(weight) # 以一维数组的形式返回方阵的对角线(或非对角线)元素,或将一维数组转换成方阵(非对角线元素为0)
self.w=np.linalg.inv(X.T.dot(weight_matrix).dot(X)).dot(X.T).dot(weight_matrix).dot(y)
return checkpoint_x.dot(self.w)
def fit_transform(self,X,y,checkArray):
m=len(y)
preds=[]
for i in range(m):
preds.append(self.fit_predict(X,y,checkArray[i]))
return np.array(preds)
if __name__=='__main__':
X=np.linspace(0,30,100)
y=X**2+2
X=X.reshape(-1,1)
lr=LocallyWeightedLinearRegression(tau=3)
y_pred=lr.fit_transform(X,y,X)
plt.plot(X,y,label='gt')
plt.plot(X,y_pred,label='pred')
plt.legend()
plt.show()
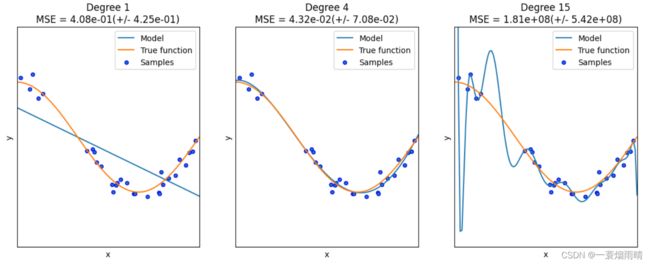
我们现实生活中的很多数据不一定都能用线性模型描述。依然是房价问题,很明显直线非但不能很好的拟合所有数据点,而且误差非常大,但是一条类似二次函数的曲线却能拟合地很好。为了解决非线性模型建立线性模型的问题,我们预测一个点的值时,选择与这个点相近的点而不是所有的点做线性回归。基于这个思想,便产生了局部加权线性回归算法。在这个算法中,其他离一个点越近,权重越大,对回归系数的贡献就越多。

线性判别分析(LDA)
参见 实现线性判别模型(numpy、sklearn)
from sklearn import discriminant_analysis
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
class LDA:
def __init__(self):
self.omega=None
self.omiga_mu_0=None
self.omiga_mu_1=None
pass
# 《机器学习》 p61
def fit(self,X,y):
n_samples = X.shape[0]
extra = np.ones((n_samples,))
X = np.c_[X, extra]
X_0=X[np.where(y==0)]
X_1=X[np.where(y==1)]
mu_0=np.mean(X_0,axis=0)
mu_1=np.mean(X_1,axis=0)
#S_omega=X_0.T.dot(X_0)+X_1.T.dot(X_1)
#invS_omega=np.linalg.inv(S_omega) # np.linalg.inv返回给定矩阵的逆矩阵
S_omega=(X_0-mu_0).T.dot(X_0-mu_0)+(X_1-mu_1).T.dot(X_1-mu_1)
invS_omega=np.linalg.pinv(S_omega)
self.omega=invS_omega.dot(mu_0 - mu_1)
self.omega_mu_0=self.omega.T.dot(mu_0)
self.omega_mu_1=self.omega.T.dot(mu_1)
pass
# 书上没讲怎么判断分类
# 采用距离度量,计算X到两个投影中心的L2距离,分类为距离更近的类别。
def predict_proba(self,X):
if self.omega is None:
raise RuntimeError('cant predict before fit')
n_samples = X.shape[0]
extra = np.ones((n_samples,))
X = np.c_[X, extra]
omega_mu = X.dot(self.omega)
d1=np.sqrt((omega_mu-self.omega_mu_1)**2)
d0=np.sqrt((omega_mu-self.omega_mu_0)**2)
prob_0=d1/(d0+d1)
prob_1=1-prob_0
return np.column_stack([prob_0, prob_1])
def predict(self,X):
p = self.predict_proba(X)
res = np.argmax(p, axis=1)
return res
if __name__=='__main__':
np.random.seed(42)
breast_data = load_breast_cancer()
X, y = breast_data.data, breast_data.target
X = MinMaxScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
lda = LDA()
lda.fit(X_train, y_train)
lda_prob = lda.predict_proba(X_test)
lda_pred = lda.predict(X_test)
#print('tinyml lda_prob:', lda_prob)
#print('tinyml lda_pred:', lda_pred)
print('tinyml accuracy:', len(y_test[y_test == lda_pred]) * 1. / len(y_test))
sklearn_lda = discriminant_analysis.LinearDiscriminantAnalysis()
sklearn_lda.fit(X_train,y_train)
sklearn_prob=sklearn_lda.predict_proba(X_test)
sklearn_pred=sklearn_lda.predict(X_test)
#print('sklearn prob:',sklearn_prob)
#print('sklearn pred:',sklearn_pred)
print('sklearn accuracy:',len(y_test[y_test==sklearn_pred])*1./len(y_test))
高斯判别分析
参考
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
"""
Gaussian Discriminant Analysis
"""
class GDA:
def __init__(self):
self.Phi=None
self.mu0=None
self.mu1=None
self.Sigma=None
self.n=None
pass
def fit(self, X, y):
m=X.shape[0]
self.n=X.shape[1]
bincount=np.bincount(y) # 统计非负整数值出现的次数。
assert bincount.shape==(2,)
self.Phi=bincount[1]*1./m
zeros_indices=np.where(y==0)
one_indices=np.where(y==1)
self.mu0=np.mean(X[zeros_indices],axis=0)
self.mu1=np.mean(X[one_indices],axis=0)
self.Sigma=np.zeros((self.n,self.n))
# for i in range(m):
# if y[i]==0:
# tmp=(X[i]-self.mu0).T.dot((X[i]-self.mu0))
# self.Sigma+=tmp
# else:
# tmp=(X[i]-self.mu1).dot((X[i]-self.mu1))
# # tmp=(X[i]-self.mu1).reshape(-1,1).dot((X[i]-self.mu1).reshape(1,-1))
# self.Sigma+=tmp
self.Sigma=(X[zeros_indices]-self.mu0).T.dot(X[zeros_indices]-self.mu0)+(X[one_indices]-self.mu1).T.dot(X[one_indices]-self.mu1)
self.Sigma=self.Sigma/m
def predict_proba(self, X):
probs=[]
m=X.shape[0]
p0=1-self.Phi
p1=self.Phi
denominator=np.power(2*np.pi,self.n/2)*np.sqrt(np.linalg.det(self.Sigma))
for i in range(m):
px_y0=np.exp(-0.5*(X[i]-self.mu0).dot(np.linalg.inv(self.Sigma)).dot((X[i]-self.mu0).T))/denominator
px_y1=np.exp(-0.5 * (X[i] - self.mu1).dot(np.linalg.inv(self.Sigma)).dot((X[i] - self.mu1).T)) /denominator
p_y0=px_y0*p0
p_y1=px_y1*p1
probs.append([p_y0/(p_y0+p_y1),p_y1/(p_y0+p_y1)])
return np.array(probs)
def predict(self, X):
p = self.predict_proba(X)
res = np.argmax(p, axis=1)
return res
if __name__ == '__main__':
np.random.seed(42)
breast_data = load_breast_cancer()
X, y = breast_data.data, breast_data.target
X=MinMaxScaler().fit_transform(X)
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
gda = GDA()
gda.fit(X_train, y_train)
lda_prob = gda.predict_proba(X_test)
lda_pred = gda.predict(X_test)
# print('gda_prob:', lda_prob)
# print('gda_pred:', lda_pred)
print('accuracy:',len(y_test[y_test ==lda_pred]) * 1. / len(y_test))
多项式回归
来自
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
def true_fun(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
degrees = [1, 4, 15] # 多项式最高次
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i],
include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)]) # 使用pipline串联模型
pipeline.fit(X[:, np.newaxis], y)
# 使用交叉验证
scores = cross_val_score(pipeline, X[:, np.newaxis], y,
scoring="neg_mean_squared_error", cv=10)
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
degrees[i], -scores.mean(), scores.std()))
plt.show()