Python:【人工智能】【机器学习】这篇博客带你读懂机器学习
博主这学期开了一门人工智能的课程,学了半学期大致对整个体系有了一定的了解。打算结合比较通俗易懂的B站up主【五分钟机器学习】的视频进行简单的阶段性总结.
一、机器学习的起点:线性回归(Linear Regression)
我们小学二年级的时候就学过 y = a x + b y=ax+b y=ax+b的数学模式,对两个精准的点可以求出公式中的 a a a和 b b b,我们就可以求的任意 x x x时候对应的 y y y 。

比如:排队的队伍、身高体重比、广告投入与销量的关系。这些实际问题虽然存在排队问题中个别在队伍外面排队的人、身高体重比问题中个别特别肥胖的人、投了广告花式作死的杜嘉班纳(D&G)这些少数特别情况的存在,但总体还是呈现一条歪歪曲曲的线符合 y = a x + b y=ax+b y=ax+b特征。
所以我们的线性回归就是在 y = a x + b y=ax+b y=ax+b这个小学问题上进行了一点点升级,由于就像上面所说的一样,实际问题不会存在所有样本都精准落在一条直线上的情况,所以我们要保证这条直线最大程度的符合实际情况。
我们称上面这些实际问题为线性问题,而对这些实际问题中新样本的预测问题就称为线性回归问题
缺点:线性回归模型作为最基本的模型就是它只能分析线性问题,对于预测股票等不符合 y = a x + b y=ax+b y=ax+b的情况就不适用于此模型。
二、机器分类的基石:逻辑回归(Logistic Regression)
还是在小学,假设你的班主任是个看了我这篇博客的人工智能爱好者,那么她在期末评选这学期三好学生的时候就会这么办:把成绩、体育、品德进行量化,然后采用给每项的加上一个权重,结合权重给每个人打上一个分数,就形成了这样一个模型 Y = a 1 × 学 习 + a 2 × 体 育 + a 3 × 品 德 + b Y=a_1×学习+a_2×体育+a_3×品德+b Y=a1×学习+a2×体育+a3×品德+b。老师再根据每个人Y值进行排序,从高到底开始发奖状和大红花。
我们先跟视频中一样,把很复杂的多元问题化简成只讲分数,那么它现在变成了这个样子 Y = a × 学 习 + b Y=a×学习+b Y=a×学习+b。是不是很眼熟,这就回到了线性回归问题。
读者1:那我们为什么不直接用这个模型解决呢?
博主:如果老师一个不注意把学生的分数打成10086,那为了拟合上那个错误的数据,整个模型都会产生很大的偏差呀,就像这样。
 读者2:那直接改回来不就好了,或者在程序里面限制输入范围不就OK啦
读者2:那直接改回来不就好了,或者在程序里面限制输入范围不就OK啦
博主:…拆台嗷,这样机器学习就没法发展了。来,我们看下一题
为了拟合好这些可能出现的错误信息,我们引入了sigmoid函数:
p = s i g m o i d ( y ) = 1 1 + e − Y 其 中 : Y = a 1 × 学 习 + a 2 × 体 育 + a 3 × 品 德 + b p=sigmoid(y)=\frac1{1+e^{-Y}}\\ 其中:Y=a_1×学习+a_2×体育+a_3×品德+b p=sigmoid(y)=1+e−Y1其中:Y=a1×学习+a2×体育+a3×品德+b

我们可以看到,这个sigmoid函数输出的值是在0~1之间。所以它也常被用来判断一件事物发生的概率,刚好可以被老师拿来预测同学们当选三好学生的概率。
小总结:
- 线性回归(Linear Regression)的输出值可以是任意值,所以可以拿来做任何线性问题的ji数值预测。→ Regression 回归算法
- 逻辑回归(Logistic Regression)的输出只在(0,1),所以很适合拿来做线性问题概率的预测。→Classification 分类算法
sigmoid函数目前被广泛的用于时间的判断,例如如果你有足够充足的信息来源和准确的权重,你可以搭建一个sigmoid函数,它会帮你预测这支股票是会涨还是跌。除此之外,还可以用于指纹识别、人脸识别和智能医疗。(这也就是为啥手机录指纹要各个方位录入好几次,每块区域都是一个 x x x)
优点:1.非常适合用来计算概率;2.能够减小极端值的影响。
缺点:用线性模型转化而来,所以也只能处理简单的线性问题。
拓展:分类问题常用的其他方法
Python:【人工智能】【机器学习】带你从零到用代码实现线性回归问题
准确率、混淆矩阵、F统计… 感兴趣先自行查一查,后面博主会写相关博客进行介绍
三、环境会影响你的决策:K邻近算法(KNN:K-NEAREST NEIGHBOR)
)
如果视频里的例子还没有理解的话,我们也可以拿是否考研为例。当你身边的80%的人都在考研的时候,如果你也会选择去考研。那么这时你的潜意识里就作为一个基本点进行了一次KNN算法,将自己也归类到与周围相同的类别中。
明白了这个算法的逻辑,那么怎么来实现它呢?首先,我们先建立一个小学三年级常用的直角坐标系(简化的欧几里得空间系),想必大家也还记得距离公式吧。
d i s ( a , b ) = ∣ ∣ a , b ∣ ∣ = ( a 1 − b 1 ) 2 + ( a 2 − b 2 ) 2 dis(a,b)=||a,b||=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2} dis(a,b)=∣∣a,b∣∣=(a1−b1)2+(a2−b2)2
现在我们有了空间,也有了距离。就可以把我们已经有的实例抽象到这个坐标系中,当把我们需要预测的实例也录入到这个空间中时,这个算法就可以求得每个待测实例周围最近的那几个点分别都是哪一类,就可以用上面的方法对我们的待测实例进行分类了。
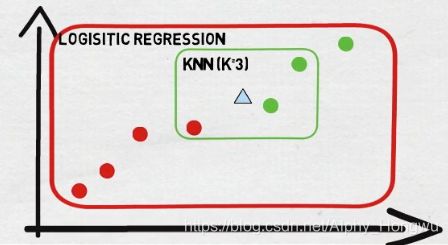
我们会发现,KNN算法也是用于分类问题的算法,类似于sigmoid函数,所以上面拓展中提到的几种常用方法也适用与本算法。
读者1:那么KNN算法可以用来干什么呢?
博主:因为它是根据实例的特征进行预测,所以可以用来做偏好推送。比如我们在应用宝下载软件后都会显示一堆相关软件的推送,这些就可以通过KNN算法归纳计算之前所有用户的喜好来实现。
读者1:所以抖音、B站的算法推送也可以用这个算法实现吗?
博主:对,是可以的!
优点:1.直观,好理解;2.可以局部估算,不需要估算整体数据
缺点:1.局部估算可能不符合全局分布;2.不能计算概率;3.对半径K的取值非常敏感
拓展:如何取得一个较合适的K值
可以采用交叉验证(cross-validation)来找到这个K来做最优的估算。
四、可视化的决策过程:决策树(Decision Tree)
我们上面讨论了三种分类、回归问题,都可以很好的得到我们需要的结果。但是如果我们想知道这中间的判断究竟是怎么来的,那么就只能依靠决策树来做这件事了。那么,究竟什么是决策树呢?
简单来说,就是提前预设好一批样本(sample)作为训练集,搭建好一种分类模型。当我们把需要预测的新样本导入到决策树中。它就会根据导入测试集的样本属性进行逐一判断,放到预测结果那一个框里。
就像图中我们把鸟、蝙蝠、飞机、狗、鸡作为训练集,而羊作为测试集放入这样的决策树就得到了“不是鸟”的预测结果。
读者3:那么这么做有什么好处呢?
博主:这样不仅可以让算法推理过程更直观,也可以方便我们对预判错误的样本进行分析。手动去调整它各个属性的权重,达到更加精准的分类效果。
读者3:这里的权重是上面提到的 y = w x + b y=wx+b y=wx+b中的 w w w吗?
博主:对,具体步骤我在这篇博客中有写。感兴趣的话跳转过去研究一下。
读者3:好嘞,我看完这篇博客就去研究。还有,我觉得这个决策树还能再优化一下。
博主:对,决策树条件的选择还是一门学问呢,我来详细讲一下吧。
我们现在引入一个信息熵(Entropy)的概念,简单来说就是衡量一个节点内容的不确定性

根据概念我们可以知道,熵越大,节点内的信息就越鱼龙混杂。所以我们要保证最后划分出的子节点的熵尽量低。这个时候我们就可以引入熵增概念:
熵 增 的 增 益 = 上 层 节 点 − 本 层 熵 的 总 和 公 式 : G ( D ) = H ( X ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ H ( D ) v 熵增的增益=上层节点-本层熵的总和\\公式:G(D)=H(X)-\sum\limits_{v=1}^V\frac{|D^v|}{|D|}H(D)^v 熵增的增益=上层节点−本层熵的总和公式:G(D)=H(X)−v=1∑V∣D∣∣Dv∣H(D)v
而这个G(D)的计算方法,就是在决策树中大名鼎鼎的ID3模型。
优点:直观,好理解;
缺点:1.对于树的最大深度这个预设参数很敏感
①.深度太大,可能过拟合(overfit);②.深度太小可能欠拟合(underfit)
2.数量量很大或数据维度很高时,计算会很慢
拓展:
1.ID3模型因为是基于已知样本的属性和类别进行搭建的分类模型,所以它不能用做回归模型。如果我们可以用Classification And Regression Tree(CART)逻辑来做回归、决策等问题。此外还有C4.5,CHAID等方法来训练决策树。
2.通常为了保证一个合理的树的深度的取值,我们也会采用与KNN算法计算K值相同的方法——交叉验证来找到最优的深度用来估算。

五、现代机器学习的血液:梯度下降法(Gradient Descent)
我们前面已经分析了线性回归和逻辑回归方法两种处理回归问题的方法。它们的根本方法就是找到一个合适的 y = A x + B y=Ax+B y=Ax+B来对使得损失函数(Loss Function)最小。而 a a a和 b b b又可以取任意值,且随着维度增加穷举的难度会以指数增加,所以我们不可能采用穷举法一个个试。
这个时候梯度下降法(Gradient Descent)就应运而生,那么什么是梯度下降法呢?

我们把函数想象成滑滑梯,当我们在下滑的时候所受到的重力会分解为下压力和下滑力。而这个下滑力会一直驱使我们向最低点滑动。这时我们将这个概念带入到Loss Function最低点的求解中:
如果我们只考虑A的值,代入到损失函数 L = S U M ( Y t r u e − Y p r e d ) 2 L=SUM(Y_{true}-Y_{pred})^2 L=SUM(Ytrue−Ypred)2中就会得到如图的函数,要求的最低点能想到最好的方法就是进行求导。我们得到导数 g = d y d x = lim △ x → 0 △ y △ x g=\frac{dy}{dx}=\lim\limits_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x} g=dxdy=△x→0lim△x△y作为下落的加速度。但因为梯度下降的曲线中,大多数函数都是平滑曲线,所以我们不能直接知道什么位置是最低点。我们只能规定一个学习步长(Learning Rate)来一步一步向最低点靠拢。
优点:逻辑递进更新求解更快,且跟Loss函数高度相关。
缺点:1.只知道导数方向,不知道最低点→对学习步长很敏感
2.函数存在多个波峰波谷,会陷入局部的谷底→无法保证全局最优性
拓展:
梯度下降法不只运用与简单的线性回归和逻辑回归。几乎现在所有的人工智能都运用了它或者它的变种算法,例如:随机梯度下降(Stochastic Gradient Descent)、批量梯度下降(Stochastic Batch Gradient Descent)、小批量梯度下降(Mini Batch Gradient Descent)


