因果推断运用到机器学习的思想 2篇论文
因果推断+机器学习
- 1. 2019《Towards The First Adversarially Robust Neural Network Model on MNIST》
- 2.2018《Invariant Models for Causal Transfer Learning》
这里主要涉及机器学习中运用因果推断的思想,论文具体细节过程不详述。
1. 2019《Towards The First Adversarially Robust Neural Network Model on MNIST》
作者: Lukas Schott1-3∗, Jonas Rauber1-3∗, Matthias Bethge1,3,4†& Wieland Brendel1,3†
发表: Published as a conference paper at ICLR 2019
![]()
问题: 针对数据集MNIST分类(0-9的数字图像分类)问题,小的扰动依旧会造成很大误差,目的增加模型的鲁棒性。
图像分类问题,共k个类,样本x的标签y真∈{1,2,…,k}。输入x,求解f(x)=p(y|x),输出f(x)为向量,表示x的预测标签y的概率分布。
本文模型: Analysis by Synthesis model (ABS) ,利用自编码器(Kingma & Welling, 2013)。
涉及因果关系: 已知样本x,求概率分布P(class|X=x)转化成学习类条件数据分布P(X|Y)。即利用贝叶斯公式求:
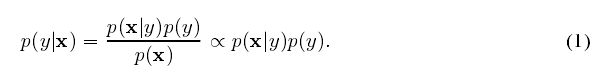
p(y)的分布可以用训练集估计。
P(x|y):利用变分自编码器(variational autoencoders ,VAEs;Kingma & Welling, 2013)(隐变量z)。
【补充:
自编码器: 目的是压缩模型(隐向量z)。输入无标签x向量,经过一个神经网络压缩成z向量,再经过一个神经网络恢复x ̃。
变分自编码器: 目的是生成模型。输入无标签x向量,经过中间隐变量z,最后生成x ̃。
补充结束】
![]()
Kingma & Welling, 2013变分自编码器,估计下界(注:有多少个类就训练多少个自编码器):
推出p(y|x)的概率:每个类都包含一个自编码器得到p(x|y)的最大下界,这里除以总共的就隐含了p(y)概率。其中η作用让标签平滑,α为缩放因子。
![]()
实验:(对图像的扰动有不同的攻击方式)
其中,Binary ABS 是把MNIST图片像素二值化。
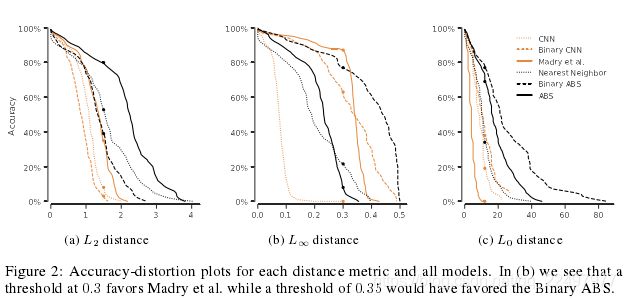
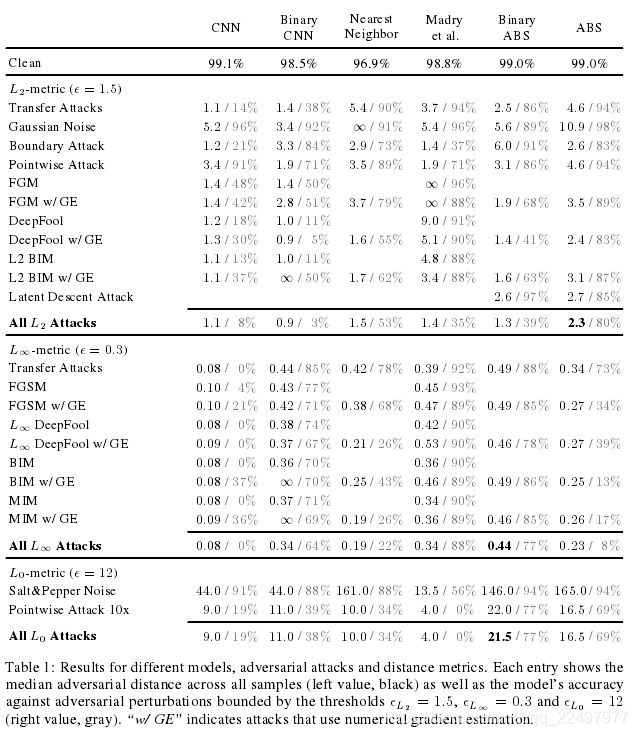
没有一个单一的攻击在所有模型上都是最好的,因此突出了广泛攻击的重要性。
思想: 其实是变分自编码器和因果有关系,这里隐变量z的输出不是代表单点值,而是表示分布,这样就能用到贝叶斯后验分布等公式。
![]()
2.2018《Invariant Models for Causal Transfer Learning》
发表: Journal of Machine Learning Research 19 (2018) 1-34
题目: 因果迁移学习的不变模型,有关多任务学习,迁移学习,领域泛化。
问题背景: 领域泛化DG/多任务学习MTL中的知识迁移。
![]()
【补充:
1. 多任务学习 (MTL,2018《A survey on multi-task learning》)

即给定 m 个学习任务,其中所有或一部分任务是相关但并不完全一样的,多任务学习的目标是通过使用这 m 个任务中包含的知识来帮助提升各个任务的性能。
2. 领域泛化DG: 目标域不可知。
补充结束】
![]()
问题: 解决训练集和测试集数据的分布不同
具体问题: 目标任务T是预测无标签样本X的值 Y∈R。
![]()
训练集:D个任务(已知D个训练集和相应标签值),服从Pk分布。![]()
方法:训练 f :X → Y,使得在任务T中下图的目标损失函数loss达到最小。![]()
![]()
![]()
思想(涉及因果): covariate shift(协变量移位):即所有任务(D个训练任务和测试任务T)中,下图条件分布不变。![]()
则不同任务的联合分布P(Xk,Yk)的差异仅在于边缘分布P(Xk)的差异。则对于任务T的训练集可以通过重要性采样进行重新加权。
创新点 :本文提出covariate shift(协变量移位)仅对特征的一个子集成立。
即(指标集S*,训练集X为p维向量)![]()
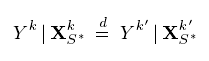
![]()

d表示均匀分布。
![]()
两个假设(需要用假设A1‘ 和A2。MTL满足,但DG只满足A1和A2,需要加额外条件):

训练网络的目标损失函数:
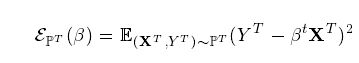
相应的定义其他任务上的损失:
![]()
给出了子集S*寻找算法(对于DG问题,S+是满足A1的集合,S+不唯一,S* 是满足A1’的集合,S^ 是S+中可以最大限度的提高在预测集上的预测精度,即最能满足A1’的;对于MTL问题,S+和S*等价)


注:不变集不一定存在。

实验没看懂,但是结论:![]()
证明了利用不变集进行预测在DG的对抗条件下是最优的。

在实践中,我们看到我们的算法是成功的,当有足够的训练任务可用时,找到一组导致不变条件的预测器。我们的方法可以合并来自测试任务(MTL)的额外数据,并在合成数据上产生良好的性能。
![]()
结合因果思想: 迁移时要求P(Yk|Xk)不变。