BP神经网络算法及Matlab实现

数据结构与算法

BP神经网络算法

1. 算法原理

1.1 概述

​ 人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。
​ BP神经网络的计算过程由正向计算过程和反向计算过程组成。正向传播过程，输入模式从输入层经隐单元层逐层处理，并转向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转入反向传播，将误差信号沿原来的连接通路返回，通过修改各神经元的权值，使得误差信号最小。

1.2 算法分析

多层神经网络结构：

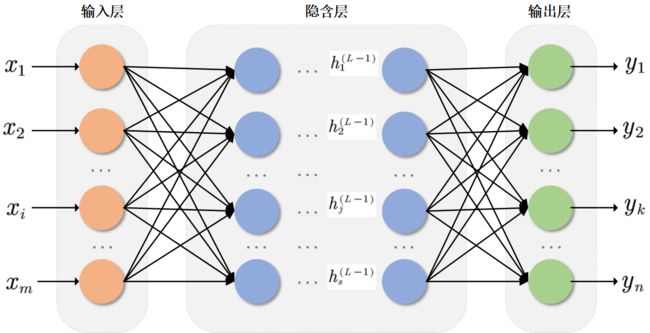
通常一个多层神经网络由$L$​​层神经元组成，第一层称作输入层，最后一层称作输出层，中间层为隐含层。

多层神经网络的基本组成元素是神经元，单个神经元的模型如下：

输入层输入向量:$X=(x_1,x_2,...，x_i,...,x_m);$​

第$l$​​​​​层的隐含层向量：$H^l=(h_1^l,h_2^l,...,h_j^l,...,h_{s_l}^l)(l=2,3,...,L-1,j=1,2,...,s_l);$​​​​

输出层输出向量：$Y=(y_1,y_2,...,y_k,...,y_n);$​

设$w_{ij}^l$为从第$l-1$层的第$i$个神经元与第$l$层的第$j$​个神经元之间的连接权重，$b_j^l$为第$l$层第$j$​个神经元的偏置。

因此得到：
$$\begin{gathered} h_j^l=f(ne{t}_j^l) \\ ne{t}_j^l=\sum _{j=1}^{s_{l-1}}{w}_{ij}^l+b_j^l \end{gathered}$$
其中$ne{t}_j^l$为第$l$层第$j$个神经元的输入，$f(\cdot )$​为激活函数。

激活函数：

作用：引入非线性因素，使得模型能够较好地逼近非线性函数。

BP神经网络算法常用的激活函数：

• Sigmod函数：
  $$f(x)=\frac{1}{1+e^x}$$
  

• Tanh函数（双曲正切函数）
  $$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

  

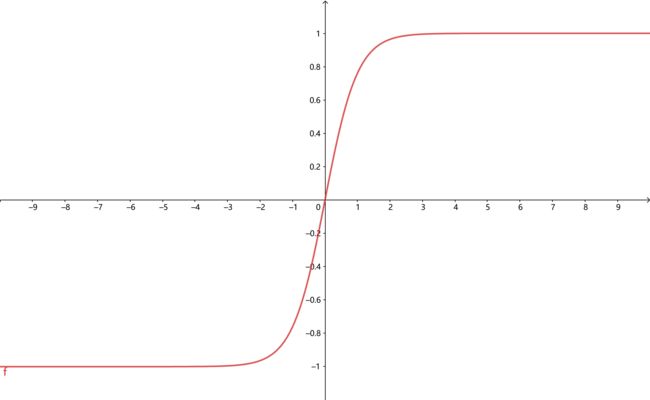
  偏置：

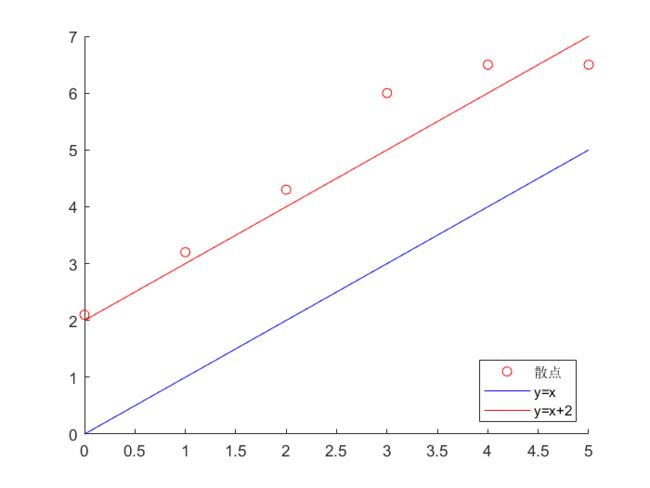
  作用：可以理解为加入一个与输入$X$无关的常数项，使得逼近的效果更好。

  

  如果用$y=x$​​​去逼近，效果不如人意，相反如果加入一个常数项，使得$y=x+2$​，效果则会好很多。

  

  误差函数:

  作用：衡量输出结果与期望输出的差距

  假设有$p$​个训练样本$\{(x(1),y(1)),(x(2),y(2)),...,(x(p),y(p))\}$​,$d(i)$​为对应$x(i)$​的期望输出，假设单个训练样本有$n$​个输出。定义误差函数：
  $$E=\frac{1}{p}\sum _{i=1}^{p}E(i)$$
  其中$E(i)$为单个样本的训练误差：
  $$E(i)=\frac{1}{2}\sum _{k=1}^n(d_k(i)-y_k(i){)}^2$$
  因此全局误差函数：
  $$E=\frac{1}{2p}\sum _{i=1}^p\sum _{k=1}^n(d_k(i)-y_k(i){)}^2$$

  如何更新权重与偏置：

  误差反向传播更新权重与偏置

  一般采用梯度下降法更新权重与偏置：
  $$\begin{gathered} w_{ij}^l=w_{ij}^l-\alpha \frac{\partial E}{\partial w_{ij}^l} \\ {b}_j^l=b_j^l-\alpha \frac{\partial E}{\partial b_j^l} \end{gathered}$$

  其中$\alpha$为学习速率，$\alpha \in (0,1)$​​。BP神经网络算法关键就在与如何求解上述两个偏导数，具体推导比较繁杂，这里就不在叙述，相关参考将附在文末²。

1.3 回顾

最后我们再通过一个示意图，回顾BP神经网络算法的整个流程。

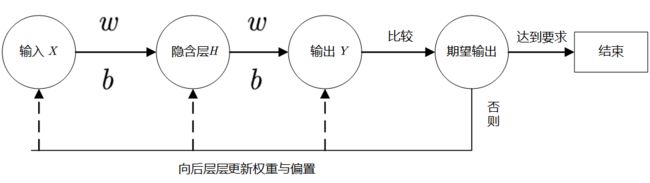
1.4 优劣势

优势：

主要用于以下四个方面：

• 函数逼近
• 模式识别
• 分类
• 数据压缩

劣势：

• 学习速度慢，需要多次学习才能收敛
• 采用梯度下降法，容易陷入局部最小值
• 网络层数、神经元个数的选取没有理论指导，主要凭借经验
• 网络推广能力有限

2. Matlab实现

2.1 算法实现步骤

(1) 进行数据预处理

(2) 建立BP神经网络模型

(3) 利用样本进行训练

(4) 返回训练结束的模型

2.2 案例

​ 在建立BP神经网络模型以及训练（即更新权重与偏置）Matlab有自带的函数，在实现BP神经网络算法的时候，我们直接调用这些函数就可以。

​ 为了能够更清晰地了解算法的实现过程，这里选取比较简单的数据进行演示。

案例一：曲线拟合

题目：创建BP神经网络

输入向量 $P=[0,1,2,3,4,5,6,7,8,9,10];$

期望输出 $T=[0,1,2,3,4,3,2,1,2,3,4];$

散点图如下：

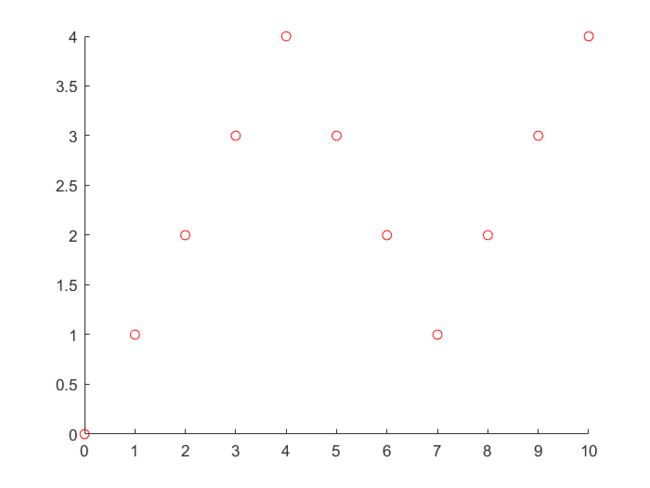
试用BP神经网络算法对上图进行拟合，并将拟合效果绘图展示。

Matlab代码：

close all; clearvars; clear; %清空工作环境
P = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
T = [0, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4];
%由于feedforwardnet函数自动对样本进行归一化和划分训练、验证、测试集,
%所以就不用手动将数据进行归一化处理，但不知道有没有打乱顺序
% n=size(P,2); temp=randperm(n); P_train=P(temp(1:8));
% T_train=T(temp(1:8)); P_test=P(temp(9:end)); T_test=T(temp(9:end));
%
% [p_train,p_input]=mapminmax(P_train,0,1);
% [t_train,t_output]=mapminmax(T_train,0,1);
% p_test=mapminmax(P_test,p_input);
net = feedforwardnet(5, 'traingd'); 
%是'5'是指隐含层有5个神经元，这里只有一个隐含层，多个隐含层神经元的个数设置为[5,3,...]

net.trainParam.lr = 0.01; %学习速率
net.trainParam.epochs = 10000; %最大训练次数
net.trainParam.goal = 1e-6; %最小误差，达到该精度，停止训练
net.trainParam.show = 50; %每50次展示训练结果
net = train(net, P, T); %训练
Y = net(P); %输出
perf = perform(net, Y, T);%误差
plot(P, T, P, Y, 'r-')

结果还不错的几个图：

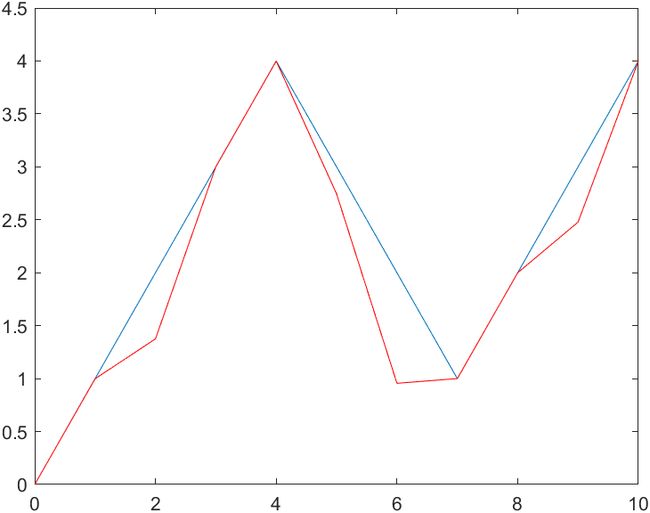
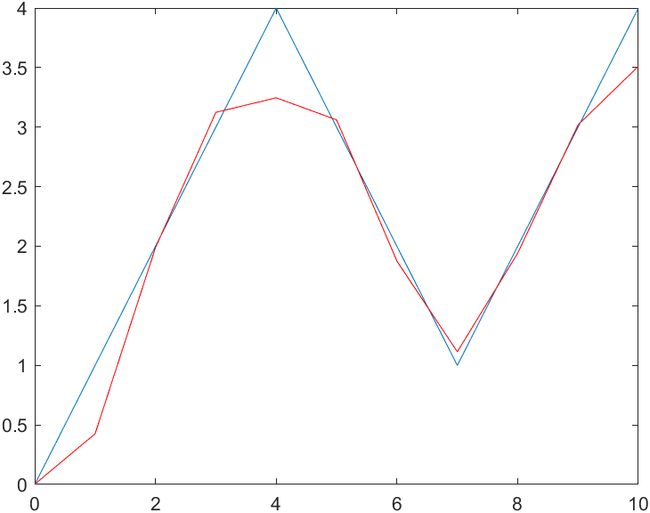
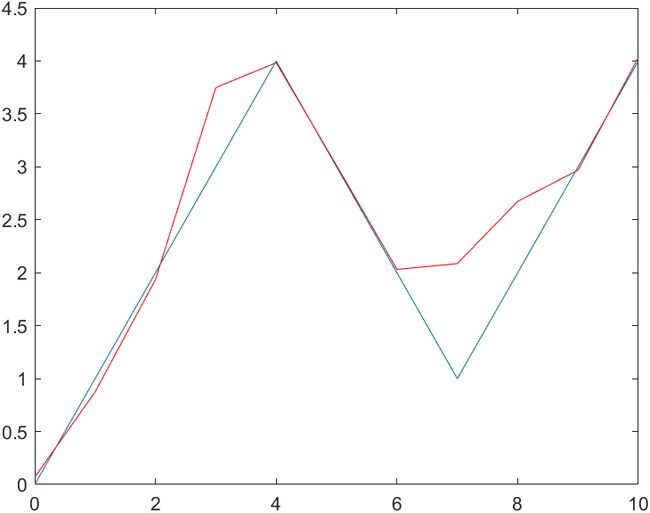
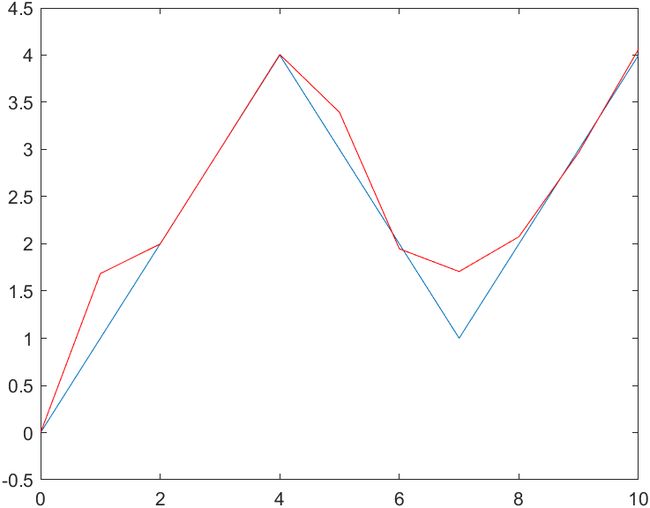
由于训练的样本太少，所以结果不是很令人满意。

案例二：蠓虫分类

题目：依据的资料是触角和翅膀的长度，已经测得了9 支Af 和6 支Apf 的数据如下：
Af: (1.24,1.72)，(1.36,1.74)，(1.38,1.64)，(1.38,1.82)，(1.38,1.90)，(1.40,1.70)，
(1.48,1.82)，(1.54,1.82)，(1.56,2.08).
Apf: (1.14,1.78)，(1.18,1.96)，(1.20,1.86)，(1.26,2.00)，(1.28,2.00)，(1.30,1.96).

试对触角和翼长分别为(1.24,1.80)，(1.28,1.84)与(1.40,2.04)的3 个标本加以识别。

Matlab代码：

clearvars; close all; %清空工作环境
%导入数据，第一列为触角长度，第二列为翅膀长度
x_1 = [1.24, 1.72; 1.36, 1.74; 1.38, 1.64; 1.38, 1.82;
    1.38, 1.90; 1.40, 1.70; 1.48, 1.82; 1.54, 1.82; 1.56, 2.08]; %Af蠓虫
x_2 = [1.14, 1.78; 1.18, 1.96; 1.20, 1.86; 1.26, 2.00; 1.28, 2.00;
    1.30, 1.96]; %Apf蠓虫
x = [x_1; x_2]'; %合并转置，因为feedforwardnet函数以一列为单个样本

goal = [ones(1, 9), zeros(1, 6); zeros(1, 9), ones(1, 6)]; %(1,0)表示为
%Af蠓虫，(0,1)表示Apf蠓虫
x_recognize = [1.24, 1.80; 1.28, 1.84; 1.40, 2.04]'; %识别的样本

plot(x_1(:, 1), x_1(:, 2), 'ro', 'DisplayName', 'Af'); %绘制Af的散点图
hold on;
plot(x_2(:, 1), x_2(:, 2), 'bo', 'DisplayName', 'Apf'); %绘制Apf的散点图
plot(x_recognize(1, :), x_recognize(2, :), 'yo', 'DisplayName', '识别' ); %绘制识别样本的散点图
xlabel('触角长度');
ylabel('翅膀长度');
legend;

net = feedforwardnet([3, 2], 'trainlm'); %两层隐含层，相应神经元个数分别为3和2，采用L-M优化算法，效果比较好
net.trainParam.max_fail = 1000; %连续1000次误差不下降，停止训练
net.trainParam.lr = 0.05; %学习速率
net.trainParam.epochs = 10000; %最大训练次数
net.trainParam.goal = 1e-15; %最小误差，达到该精度，停止训练
net.trainParam.show = 50; %每50次展示训练结果
net = train(net, x, goal); %训练
y0 = sim(net, x) %输出
perf = perform(net, goal, y0)%误差
ym = sim(net, x_recognize) %识别

下图是蠓虫的散点图，可以看出这三个样本还是比较难分类的，肉眼几乎很难判断。利用BP神经网络算法得到的结果有时候也会有比较大的差异，这也很正常，仅通过触角和翅膀长度确实不易分辨。

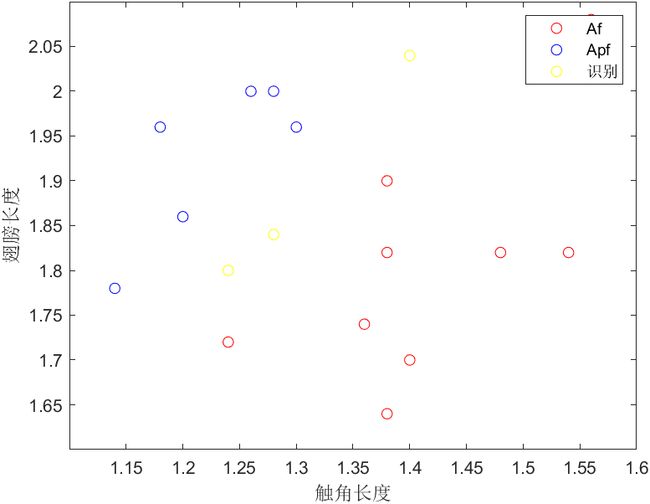
这是训练误差比较低情况下的一个输出，显示识别样本中第一、第二为Af类型的蠓虫，第三为Apf类型的蠓虫。

3. 参考来源

[1] BP神经网络_百度百科 (baidu.com)

[2] BP神经网络推导过程详解 - Alex Yu - 博客园 (cnblogs.com)

[3] 专题 通过四个matlab建模案例彻底精通BP神经网络_哔哩哔哩_bilibili

[4] 最容易听懂的BP神经网络教程----萌新入门首选课_哔哩哔哩_bilibili