机器学习笔记(7)——神经网络初探
上一篇:机器学习笔记(6)——过拟合与正则化
之前我们已经学完了基本的线性回归与逻辑回归算法以及相关的正则化技巧,下面我们就要进入令人激动的神经网络的世界
前言
之前我们讲线性回归和逻辑回归举的例子中样本都只有少数几个特征,现在我们来看一个如下有100个原始特征的分类问题(下面的样本分布图只是一种抽象的表述,不必在意,高维空间也画不出来),如果想要拟合出比较好的决策边界,我们可能需要加入很多多项式,使得最终拟合函数中有成千上万个特征,这计算起来就很复杂了
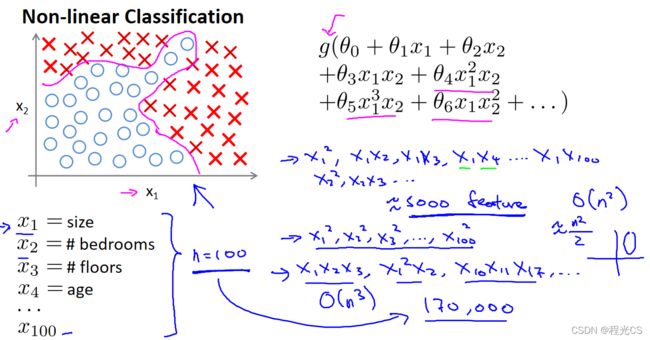
而机器学习中的问题通常都有大量的特征,如果你觉得100个特征用逻辑回归似乎也还能处理,那么下面我们再来看一个计算机视觉中的一个经典问题——汽车图片识别,我们之所以看到一张汽车图片时能识别出汽车,是因为我们的视网膜接收到这片光信号后转换为电信号,然后传输给大脑的神经网络进行特征分析卷积处理,最后得出汽车的概念,但是对于计算机本身来说一张图片就是一片像素点矩阵,不同的图片对于计算机而言就是不同大小的像素点矩阵以及矩阵中像素点值的不同(也就是还停留在视网膜接收光信号转换为电信号的阶段),例如下图中汽车图片的一个门把手,对于计算机而言就是一个包含不同像素强度值的像素点矩阵(但这个矩阵中的像素强度值肯定是某种特别的分布,我们人眼才会识别出这是一个门把手)。那么计算机视觉要做的通过大量不同的样本图片进行学习,建立一个分类器,分析图片中每个区域块的像素强度特征,以此来分类图片中是否有汽车

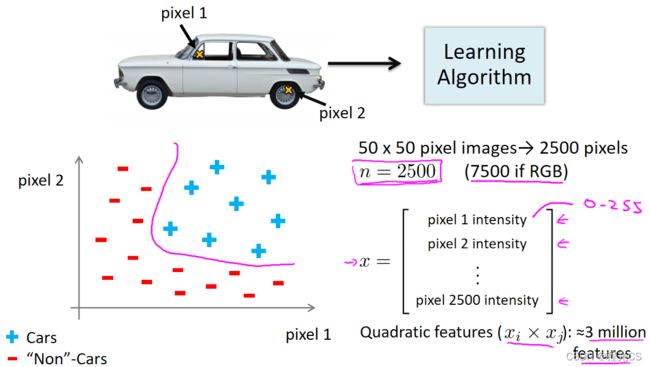
如下图,假设从每个样本图片中选择同样位置的两个像素点的强度值pixel 1和pixel 2作为图片的特征,那么我们可能最终会发现汽车图片和非汽车图片在特征空间中分布在不同的区域,我们就可以通过一个非线性假设拟合出预测函数。然而就算图片只有50x50像素,也有2500个特征(如果是RGB彩色图片,即每个像素点由三个值构成,那么就有7500个特征),如果我们要通过包含所有的二次项特征(就是前面讲的多项式特征,x1x2这样,很容易得出共有C22500项)来做逻辑回归,就有近300万个特征了,那不知道要计算多久才能迭代出总代价函数的最低点了,因此我们就需要一种算法能够处理有巨量特征的机器学习问题,能够像我们的人脑一样快速的判断出一张图片中的信息,这就是神经网络
一、神经网络(Neural Networks)思想的起源
神经网络的思想其实早在上个世纪四五十年代就出现了,最开始是想通过模仿大脑思考的方式来制造出类人智能算法,在八九十年代被广泛使用,九十年代后期由于各种原因(比如神经网络的计算量较大,当时计算机算力不够)应用逐渐减少了,但随着近年来机器学习的火热,以及计算机算力的提升使得大规模神经网络得以运行,神经网络又得到了广泛的应用和发展。
神经网络的思想起源于大脑,而人类的大脑是如此神奇,可以处理声音、处理触觉、处理图像等,如果我们想模仿大脑是否就要编写上千个复杂程序来分别模拟这些功能呢?其实不然,我们可以假设大脑只使用了一种学习算法来实现这些功能,而且这种假设也是有相关证据的,我们能听到声音是因为耳朵收到声音信号后将信息传递给了大脑中专门处理声音的听觉皮层进行处理,而科学家们曾经在动物身上做过一种叫神经重连的实验,把动物耳朵到听觉皮层的神经切断,然后将视觉神经连接到听觉皮层上,发现听觉皮层会学会看这一功能(也就是能处理图像),这就引申出一个理念:如果一块脑组织能处理光、声音和触觉信号,那么也许就存在一种学习算法,可以同时处理视觉、听觉和触觉信息,而不是需要上千种算法来模拟大脑的各种功能。
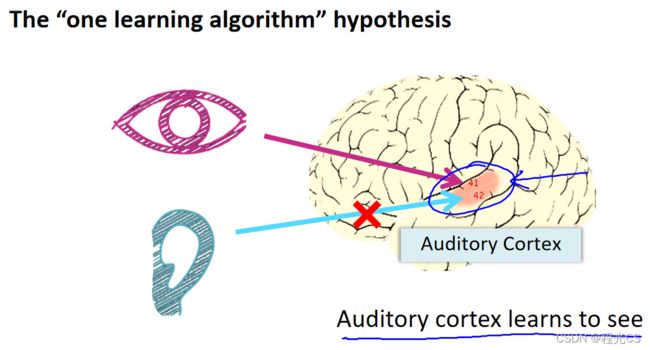
漫谈:我们可以这样假设,对于大脑来说声音信号、视觉信号、触觉信号等都属于“信号”这一大类,耳朵、眼睛、皮肤等这些功能部位接收到这些不同类别的信息后经过各自的转换接口向上转型为“信号”大类的对象然后交给大脑皮层处理,因此让其他一个功能的大脑皮层处理其它类型的信号时经过学习适应也能处理,不会出现完全不兼容的情况,是不是有一点面向对象的感觉了?(当然这只是我思维漫游时的一种猜想,扯远了hh)
二、大脑神经元的工作原理
俗话说,大道至简,前面我们说了大脑各种复杂的功能可以抽象为一块脑组织进行处理,而复杂的脑组织的工作单元也主要是由大量简单(抽象的简单)的神经元构成,现在我们就来看下大脑的最小计算单元——神经元的工作原理。
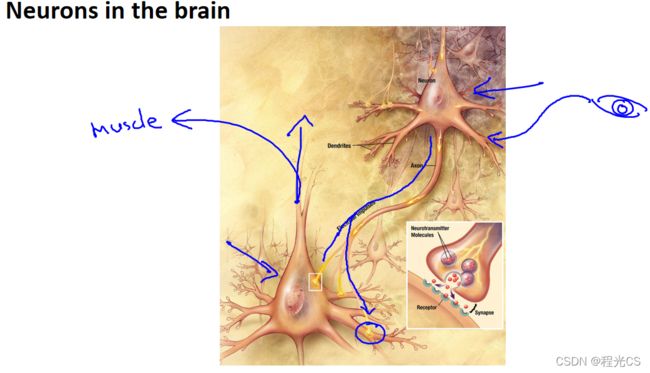
如下是一个大脑神经元细胞(Neuron)的主体结构,它有许多可以接收信息的输入通道树突(Dendrite),可以接收来自其它神经元的信息;负责对接收的信息进行变换处理的细胞体(Cell body);一条用来输出计算出的信息的通道轴突(Axon),可以向其它神经元传递信号。神经元从输入通道接收一定数目的信息,然后经过细胞体的计算,最后通过输出通道将结果传递到其它节点,这就是一个神经元的工作原理。
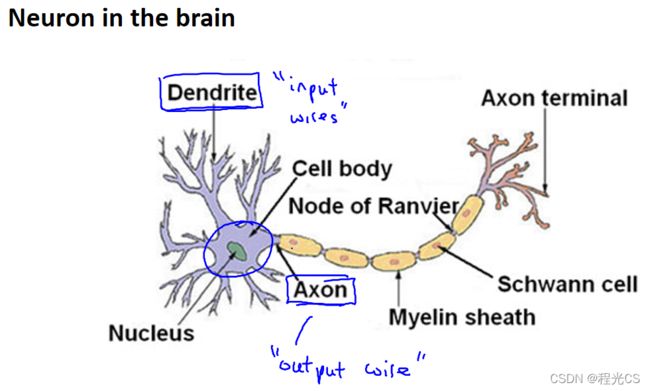
下面是一组神经元的示意图,神经元的轴突连接着其它神经元的树突,如果一个神经元需要与另一个神经元沟通,就通过轴突给另一个神经元传递电流信号,另一个神经元通过树突接收到信号后就进行计算然后执行下一步的动作,这就是我们人类思考、感知和刺激肌肉工作最基本的原理,大道至简如此
三、模拟神经元的模型
那么我们很容易就可以将上述神经元抽象为一个逻辑单元,现在我们用一个简化的神经元模型来模拟我们之前学过的逻辑回归的预测函数,如下图,它可以接收三个输入,每条输入通道上可以有一个权重系数w(也称为参数,就是将输入乘以一个系数再传递给计算单元),然后经过称为激活函数(Activate Function)的计算单元g(z)的计算后,最后通过输出通道输出一个值。这就是神经网络算法中最基本的运算单元
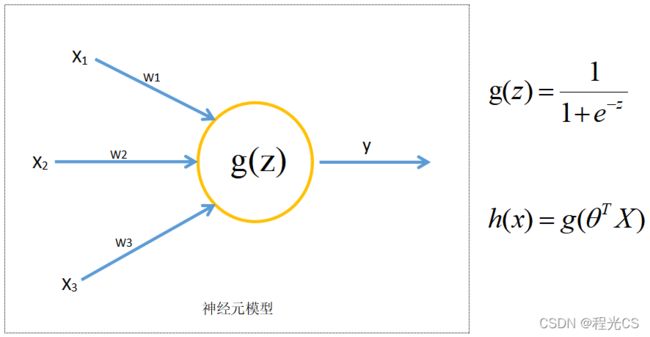
但有人可能会想,这看起来好像没有什么神奇的,不就是把之前学的函数换了一个形式表述嘛,但这就就像大脑的神经元一样,明明单个结构看起来挺简单的,组合在一起却能完成非常复杂的功能。那么现在我们就来看下多个神经元构成的神经网络的结构
如下图的神经网络,网络中的第一层即前三个输入称为输入层(input layer),最后一层的神经元称为输出层(output layer),输出最终的计算结果,而包含三个神经元的第二层称为隐藏层(hidden layer),其中每个神经元都有自己的激活函数,它们接收后面传递过来的数据信息,经过计算后再传递给下一层的神经元。这种输入经过中间隐藏层神经元计算转化不断向前传播,最后经过输出层神经元计算得到最终结果的神经网络就叫前馈神经网络,这种传播方式也叫前向传播(Forward Propagation,FP)

神经网络的结构可以有很多种,比如如下神经网络有两个隐藏层,Layer3接收Layer2的计算结果作为输入然后计算压缩出更复杂的特征(也称为隐藏特征,在某些模型中可以用中间的隐藏特征得出一些有趣的结论),最后汇聚到输出层计算出最终结果。
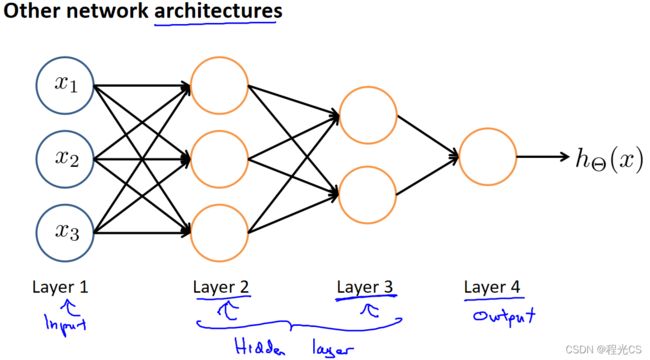
旁白:目前我们可能还很难直接体会到神经网络这种结构的妙处,但是应该能隐约感觉到,这是一个样本特征值流动、转换、信息压缩最后提取汇集成一个我们想要的特征的过程,就像我们看一张汽车图片,图片上有很多特征,但是最后在我们脑中汇集成了汽车这一概念,相比于逻辑回归,神经网络这种算法是不是更符合我们人类思考的模式呢?并且相比于逻辑回归直接一个式子,这种结构拆分成了多层函数来处理,我们还能在中间做观察和调整,就显得了更加精妙和更多的可能性。不过只有经过后续大量的实战后我们才能比较明确的认识到神经网络的作用,现阶段只需要记住它的大概形式即可。
四、神经网络的简单例子
下面我们就用神经网络的结构实现几个简单的分类器。如下图左样本分布(下图右的简化版本),每个样本有x1、x2两个特征,我们可以看出来它是大概满足y = x1 XNOR x2这样一个异或非(XNOR,即相同时取1,不同时取0)函数的
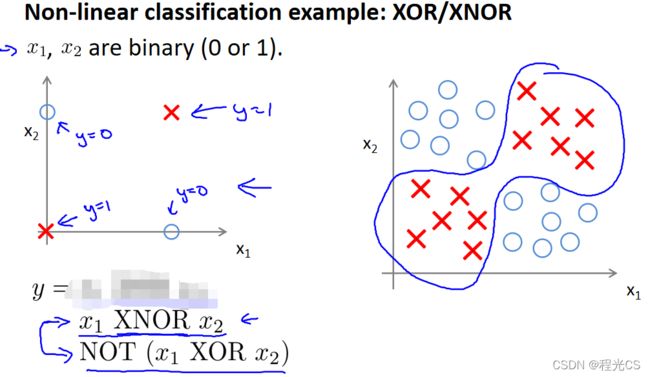
那么我们在神经网络中实现对输入的异或非呢?我们知道异或非的运算规则是 (a ∧ b) ∨ (¬a ∧¬b),那么我们就先分别来看与、或、与非是怎样实现的
1. 神经元实现与(AND)运算
首先我们加入一个偏置单元(bias unit)即常数特征1,通过推算可得出当这三个输入的权重参数分别为-30、20、20时,即激活函数g(z)=g(-30+20x1+20x2),可以将样本分为两类,一类(至多只有一个特征为1的)样本输出值接近0,另一类(特征x1、x2都为1的)样本输出值接近1,这就实现了类似与(x1 AND x2)的运算
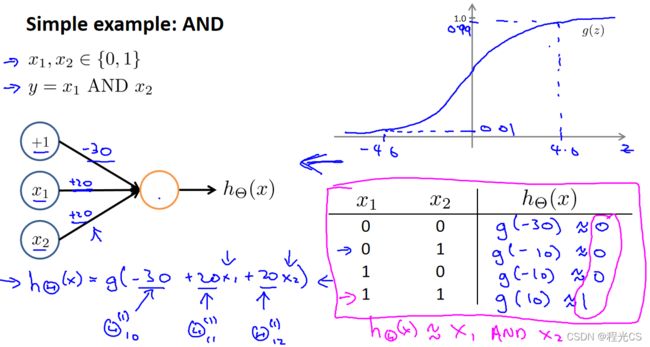
2. 神经元实现或(OR)运算
通过调整上述神经元的权重参数,同样可以实现类似或(x1 OR x2)的运算,如下
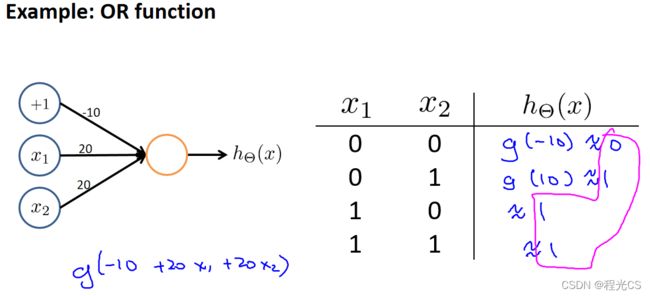
3. 神经元实现与非(NAND)运算
有了上述经验我们很容易就能得出非运算就是给输入值x乘上一个较大的负权重,这样当x为0时激活函数g(z)输出值就接近1,当x为1时g(z)输出值就接近0。那么与非运算就是特征值x1、x2都乘上一个较大的负权重,那么只有当x1、x2同时为0时输出值才为1
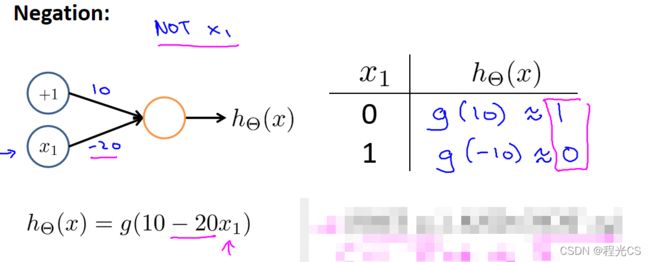
4. 神经元组合成神经网络实现XNOR分类
有了上述三个神经元,我们就可以将它们组合起来实现异或非运算。如下图,隐藏层的 与运算神经元 和 与非神经元 接收输入层输入然后计算输出,输出层的 或运算神经元 接收来自隐藏层的三个输入(还有一个是偏置神经元输出为常数1),最后计算输出结果。这样我们就实现了一个小型的神经网络,可以对样本进行XNOR分类,当样本有且只有一个特征的值为1时,它的输出值接近0,当样本的两个特征同时为0或同时为1时,它的输出值接近1。
神经网络就是这样接收输入,然后通过第一层隐藏层计算出一系列特征,再通过前面的隐藏层计算出更复杂的特征,最后归纳到最后一层计算出结果,体会到了吗?
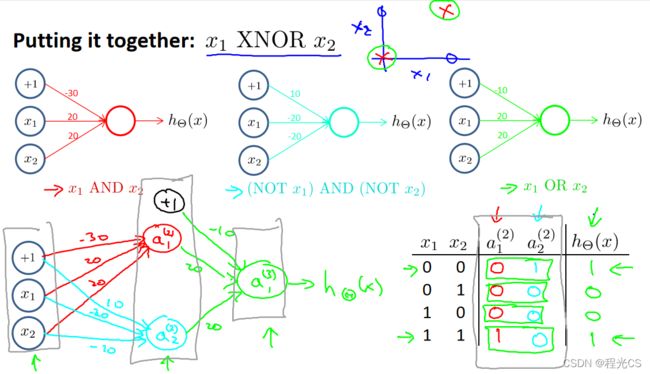
旁白:可能有人会想了,不就是一个异或非嘛,干嘛弄得这么复杂?不要忘了这是为了实现我们开始那个简化版样本分布的分类器(而且这个网络也不是真正的异或非,输出的结果不是精确的0和1而是为1的概率),我们完全可以通过灵活调整这个网络中的参数实现对那个更复杂的样本分布的分类,这就是这个网络结构的意义所在。
五、用神经网络进行多元分类
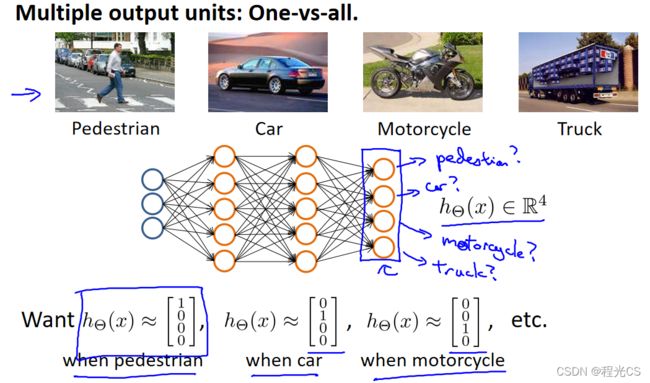
神经网络还有一个显著优点就是可以同时进行多元分类,而不仅仅是二分类。如下图我们的样本中有四类图片,分别是行人、汽车、摩托车和货车,这样的图片分类就是一个四分类问题,我们只需要通过设计网络结构让输出层有四个神经元,每个神经元输出为一类图片的可能性,这样我们就实现了同时多分类。
到这里我们已经掌握了神经网络的大体结构,那么对于一个实际的问题我们应该如何设计中间的隐藏层,如何得到合适的权重参数呢?且听下回分解