强化学习笔记(5)之时序差分法
强化学习笔记(5):时序差分法求值函数
标签(空格分隔): 未分类
文章目录
- 强化学习笔记(5):时序差分法求值函数
-
- 时序差分法与动态规划法和蒙特卡洛法的区别
- TD方法的反演
- 同策略的时序差分法:SARSA
-
- SARSA的收敛性
- SARSA($\lambda$)
-
- 异策略的TD法
时序差分法与动态规划法和蒙特卡洛法的区别
动态规划法(DP): 需要状态模型,即状态转移矩阵 P s s ′ a P_{ss'}^a Pss′a,状态值函数的估计是自举的(bootstrapping),即当前状态值函数的更新依赖于已知的其他状态值函数。
蒙特卡洛方法(MC): 可以从经验中学习,不需要环境模型;状态值函数的估计是相互独立的,但是只能应用于episode-task。
时序差分法(temporal difference learning, TD learning): 结合了DP和MC方法,并且兼具了两种算法的优点,它不需要环境模型,属于model-free算法,但它有不局限于episode-task,可以用于连续的任务。
相比于动态规划法(DP),TD 方法不需要环境模型,与MC方法一样。相比于MC方法,TD方法可以采用在线的、完全增量式的实现方式:
在MC方法中,必须要等到,episode结束,有了return之后才能更新,在有些应用中episode的时间很长,甚至有些应用环境是连续型任务,根本没有episodes。
而TD方法不需要等到最终真实的return,并且TD方法可以保证收敛到 V π V_{\pi} Vπ。
时序差分法和蒙特卡洛方法都是使用经验来解决预测问题,给定服从规则 π \pi π的一些经历,两种方法都可以跟新每一个非终止状态 S t S_t St的 V π V_{\pi} Vπ。
蒙特卡洛方法要等到return(回报)知道之后才将其设为是 V ( S t ) V(S_t) V(St)的目标值。基于增量式的蒙特卡洛方法中的V值计算方式:

时序差分学习是模拟(或者经历)一段序列,每行动一步或几步,根据新状态的价值,然后估计执行前的状态价值。
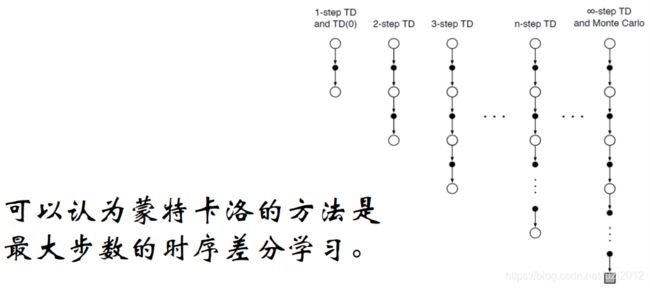
TD方法只需等 到下一个time step即可,即在时刻T+1时,TD方法立即形成一个target,并使用观测到的Reward R t + 1 R_{t+1} Rt+1和估计的 V t + 1 V_{t+1} Vt+1进行更新。最简单的TD方法称为TD(0),其更新方法为:

TD方法与MC方法一样,都是基于已有的估计进行更新,只不过MC方法更新的目标值为 G t G_t Gt,而TD更新的目标值为 R t + 1 + γ V ( S t + 1 ) R_{t+1}+\gamma V(S_{t+1}) Rt+1+γV(St+1),这两者的之间的关系,如下:
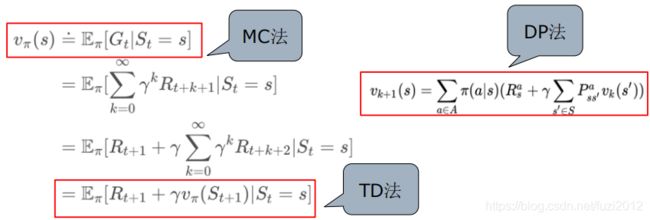
用与策略评价的TD(0)伪代码:

TD方法的反演
TD(0)方法的反演图,如下:

它对上面的节点的value评估值的更新是基于从它到下一个状态的一次样本转换;TD和MC都是更新采样反演(sample backup),因为它们都涉及到采样的连续的状态或者状态对。采样反演(sample backups)与DP的全量反演(full backups)的不同在于,它利用的不是所有可能的转换的完全分布,而是一个单一的样本转换。
现在再来看这三张图,是不是更加能理解?
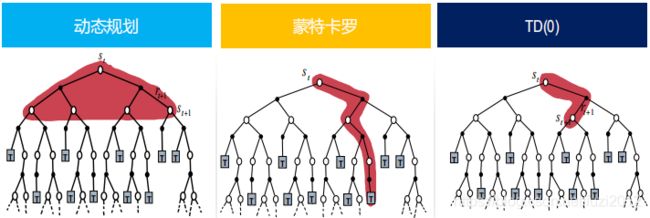
TD误差与MC误差: TD误差(TD error)用 δ t \delta_{t} δt表示,它表示的就是zai在该时刻估计的误差,在TD(0)中它指的是 R t + 1 + γ V ( S t + 1 ) R_{t+1}+\gamma V(S_{t+1}) Rt+1+γV(St+1) 与 V ( S t ) V(S_t) V(St)的差:
![]()
而蒙特卡洛误差(MC error)可以写作一系列TD error的和。

同策略的时序差分法:SARSA
与蒙特卡洛方法一样,TD的控制方式也分为同策略(on policy)和异策略(off policy)。
对于同策略(on policy): 首先要对当前的行为规则 π \pi π估计所有状态的s和行为a的 q π ( s , a ) q_{\pi}(s,a) qπ(s,a),估计的方法与上面阐述的学习 V π V_{\pi} Vπ的方法一致,每一个episode是有一系列states和state-action对组成的转换序列:

从一个“状态-行为对”到另一个“状态-行为对”的转换,根据上面对 V π V_{\pi} Vπ的估计方法, q π ( s , a ) q_{\pi}(s,a) qπ(s,a)估计值的更新方程:
![]()
每次从一个非终止状态 S t S_t St进行转换都会利用上面的更新方程来更新 Q ( S t , A t ) Q(S_t,A_t) Q(St,At),注意到该方程中有五个元素: ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) (S_t,A_t,R_{t+1},S_{t+1},A_{t+1}) (St,At,Rt+1,St+1,At+1),因此称这种方法为SARSA。
一个agent处在状态S,在这个状态下,它可以尝试各种不同的行为。当遵循某一策略时,会根据当前策略选择一个行为A,个体实际执行这个行为,与环境发生实际交互,环境会根据其行为给出即时奖励R,并进入下一个状态S’。在这个后续状态,在次依据当前策略产生一个行为A’。此时,个体并不执行该行为A’,而是通过当前的行为价值函数得到该“状态-行为对”(S’,A’)的价值Q。利用该价值同时结合个体在S状态下采取行为A所获得的即时奖励来更新个体在S状态下采取行为A的状态行为价值。
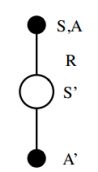
SARSA的收敛性
能使SARSA算法收敛至最优策略和最优价值函数的条件是:
1.行为策略满足GLIE特性,GLIE特性即在有限的时间内进行无限可能的探索:一是所有状态-行为对会被无限次探索,即确保探索到了所有的状态和行为;二是另外随着采样趋向无穷多,策略收敛至一个贪婪策略。
2.学习率参数 α \alpha α满足:

基于SARSA方法就可以得到同策略的控制方法(on-policy control algorithm),对于所有on-policy 方法,在持续对行为规则 π \pi π估计 q π q_{\pi} qπ的同时,也依据 q π q_{\pi} qπ采用贪婪的方式来修改行为规则 π \pi π。SARSA算法的伪代码如下:

在SARSA算法中,Q(S,A)的值存储在一张大表中,不适合解决规模很大的问题;对于每一个状态序列Episode,在状态S时采取行为A是基于当前策略的,同时该行为也是实际Episode发生的行为。在更新状态行为对(S,A)的价值循环里,agent并不实际执行在S’下的A’行为,而是将行为A’留到下一个循环中执行。
SARSA( λ \lambda λ)
根据前面的n-步收获,类似可以引入一个n-步的SARSA的概念。

这里对应的是一个状态-行为对,表示某个状态下采取某个行为的价值大小。
第n-步Q回报(Q-return)
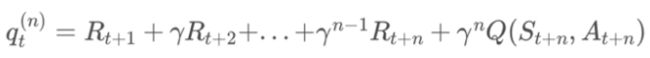
这里的n-步Q收获,Q是包含行为的,也就是某一策略下基于某一状态的行为。这样,可以把n-步SARSA用n-步Q收获来表示,如下公式:
![]()
每一步都有一个q(n),可以考虑用加权的方式融合这n个估计值(有些资料讲到前向计算n步融合加权的q(n),误导我了,愣是没看懂,什么意图。),但是SARSA( λ \lambda λ)并没有这么做,而是利用当前获得q(n)值去更新前面n步的状态行为对(Q(s,a),首先引入了Eligibility trace(适合度轨迹)的概念,用 E E E表示,是一个关于行为-状态对(s,a)的矩阵,记录经历过的状态-行为对的关系,它是用来保存在路径中所经历的每一步,因此在每次更新时也会对之前经历的步进行更新。
其值为:
![]() 初始状态时,所有的值赋值为0;
初始状态时,所有的值赋值为0;
![]() 当 S t = s , A t = a S_t=s,A_t=a St=s,At=a时,令 E t ( s , a ) + 1 E_t(s,a)+1 Et(s,a)+1,随后所有的状态-行为对都递减,即对E矩阵的所有制执行 γ λ E ( s , a ) \gamma \lambda E(s,a) γλE(s,a);
当 S t = s , A t = a S_t=s,A_t=a St=s,At=a时,令 E t ( s , a ) + 1 E_t(s,a)+1 Et(s,a)+1,随后所有的状态-行为对都递减,即对E矩阵的所有制执行 γ λ E ( s , a ) \gamma \lambda E(s,a) γλE(s,a);
![]()
引入Eligibility trace(适合度轨迹)后,SARSA( λ \lambda λ)的Q值更新公式如下:
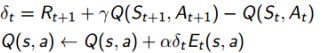
再看一下伪代码,你就知道它是怎么实现的了:

看代码注意两点:(1)当前的E值更新, E ( S , A ) ← E ( S , A ) + 1 E(S,A) \leftarrow E(S,A) + 1 E(S,A)←E(S,A)+1 ,就是在当前的状态-行为对执行的时候更新的;
(2)然后对其所有的状态的-行为对执行 E ( s , a ) ← γ λ E ( s , a ) E(s,a) \leftarrow \gamma \lambda E(s,a) E(s,a)←γλE(s,a),慢慢地这么执行下去,经历的越多的状态行为对,E值就会越大。
参数lambda取值范围为[0, 1] ,如果 lambda = 0,Sarsa( λ \lambda λ) 将退化为Sarsa,即只更新获取到 reward 前经历的最后一步;如果 lambda = 1,Sarsa(lambda) 更新的是获取到 reward 前的所有步。lambda 可理解为脚步的衰变值,即离有价值的状态越近的步越重要,越远的步则对于获取有价值的状态不是太重要。
再看看莫烦的博客的图:
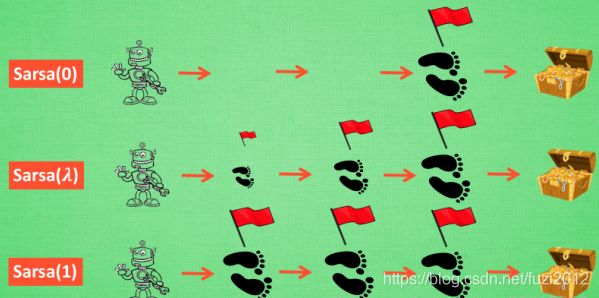
当前更新的时候,更新了所有的状态行为值(Q(s,a)),但是距离目标越近的状态行为值越大。
引入Eligibility trace(适合度轨迹)后,Sarsa( λ \lambda λ)将可以更加有效的在线学习,因为没有必要学习完整的episode,数据用完就扔掉。属于增量式的方法。
异策略的TD法
异策略的TD学习任务就是使用TD方法在目标策略 π ( a ∣ s ) \pi (a|s) π(a∣s) 的基础上更新行为价值,由于前面的文章中给出,其行为价值优化方式为:
![]()
由前面的文章中讲到过,异策略分为行为策略和目标策略,行为策略为智能体agent执行的策略,目标策略为行为价值更新的策略,对于上式,agent智能体处于状态 S t S_t St中,基于行为策略 μ \mu μ产生一个行为 A t A_t At,智能体agent执行该行为后进入状态 S t + 1 S_{t+1} St+1。
异策略学习要做的事情就是,比较目标策略和行为策略在状态 S t S_t St下产生同样的行为 A t A_t At的概率比值。
如果这个比值比较接近1,说明两个策略在状态 S t S_t St下采取的行为 A t A_t At的概率差不多,此次对于状态 S t S_t St价值的更新同时得到两个策略的支持。
如果这个概率比值比较小,表明目标策略 π \pi π在状态 S t S_t St下选择行为的 A t A_t At的机会比较小,此时为了目标策略的学习,则认为这一步的状态价值的更新布套符合目标策略,因而在价值更新是会打折扣(这个概率比值则为一个折扣因子)。
类似的,如果这个概率比值大于1,说明按照目标策略选择行为 A t A_t At的几率大于当前行为策略产生 A t A_t At的概率,此时,对当前的状态价值更新就可以更大胆一些。
从以上的分析中看出,选择一个大的概率比值是一个不错的选择。
从而得出Q_learning的伪代码:

Q_learning的反演图如下:
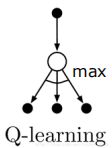
因为该规则更新是一个状态行为对,其端点是一个action node,并且该规则是在该状态下所有可能的行为中选择Q值最大的action node,所以该图下面是所有的action node。
由于Q_learning并不关心agent行为遵循什么样的策略,而仅仅采取Q值最好的行为来执行,其中的学习规则与执行规则不同,因此这是一个off-policy学习算法。
对比SARSA方法:
![]()
SARSA只需要执行动作 A t + 1 A_{t+1} At+1去得到 S t + 1 S_{t+1} St+1就能更新状态行为值。
Q_learning方法:
![]()
需要遍历在状态 S t S_t St下所有可能的行为,从中选择Q值最大的行为来更新状态行为值。所以Q_learning与SARSA的区别在于:Q_learning采取Q值最大值去更新状态行为,也就是说与当前执行的行为 a t a_t at时采用的策略无关。
当然,Q_learning还有很多毛病,导致有很多升级版本,这里就不多赘述了。