实验四 图像复原及几何校正

一、实验目的：
1.掌握退化模型的建立方法。
2.掌握图像恢复的基本原理。
二、实验原理（略）

三、实验步骤（包括分析、代码和波形）
首先来看看这个实验的内容。实验主要内容如下：
（1）选择一幅清晰的灰度图像，对该图像进行模糊化处理并加入高斯噪声，然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对退化图像进行复原，比较各种图像的复原方法的复原效果。
（2）选择一幅清晰的灰度图像，对该图像进行仿射变换，如然后分别采用连接点选择、空间变换和灰度插值法对几何失真的图像进行复原，比较各种图像复原方法的复原效果。

下面是第(1)小题的代码。
代码一：

%% 仿真逆滤波、维纳滤波，约束最小二乘滤波
close all;
clear all;
clc;
% Display the original image.
I = imread('flower.jpg'); 
[d1,d2,d3] = size(I); 
if(d3 > 1) 
I = rgb2gray(I);
end
I = im2double(I);
[hei,wid,~] = size(I);
subplot(3,3,1),imshow(I);
title('Original Image ');
 
% Simulate a motion blur.
LEN = 50;
THETA = 11;
PSF = fspecial('motion', LEN, THETA);
blurred = imfilter(I, PSF, 'conv', 'circular');
subplot(3,3,2), imshow(blurred); title('Blurred Image');
 
% Simulate additive noise.
noise_mean = 0;
% noise_var = 0.00001;
noise_var = 0.0001;
blurred_noisy = imnoise(blurred, 'gaussian', ...
                        noise_mean, noise_var);
subplot(3,3,3), imshow(blurred_noisy)
title('Simulate Blur and Noise')
 
%% 使用自带的 deconvwnr 进行维纳滤波。 deconvreg进行约束最小二乘滤波
% deconvwnr 维纳滤波，如果没有参数NSPR，则为逆滤波
 
%自带 逆滤波 对已添加噪声图像 deconvwnr
deblurred4 = deconvwnr(blurred_noisy,PSF);
subplot(3,3,4), imshow(deblurred4); title('deconvwnr逆滤波 对 运动+噪声')
 
%自带 维纳滤波 对已添加噪声图像 deconvwnr
deblurred4 = deconvwnr(blurred_noisy,PSF,0.005); %0.005为噪声信号比
subplot(3,3,5), imshow(deblurred4); title('deconvwnr维纳滤波 对 运动+噪声')
 
%自带的 deconvreg 进行约束最小二乘滤波
subplot(3,3,6);
imshow(deconvreg(blurred_noisy, PSF,20)); %20 为噪声功率
title('deconvreg最小二乘滤波 对 运动+噪声');
 
%% 自写 逆滤波,约束最小二乘滤波
 
%自写 逆滤波 对未添加噪声图像
If = fft2(blurred);
Pf = psf2otf(PSF,[hei,wid]);
deblurred = ifft2(If./Pf);
subplot(3,3,7), imshow(deblurred); title('逆滤波 对 仅运动')
%自写 逆滤波 对已经添加噪声图像
If2 = fft2(blurred_noisy);
deblurred2 = ifft2(If2./Pf);
subplot(3,3,8), imshow(deblurred2); title('逆滤波 对 运动+噪声')
 
% Try restoration using  Home Made Constrained Least Squares Filtering.
% 自写约束最小二乘滤波
p = [0 -1 0;-1 4 -1;0 -1 0];
P = psf2otf(p,[hei,wid]);
 
gama = 0.001;
If = fft2(blurred_noisy);
 
numerator = conj(Pf);
denominator = Pf.^2 + gama*(P.^2);
 
deblurred2 = ifft2( numerator.*If./ denominator );
subplot(3,3,9), imshow(deblurred2)
title('约束最小二乘滤波');
 

代码二：
㈠约束最小二乘滤波的MATLAB代码

clear all;
clc;
% Display the original image.
I = imread('flower.jpg'); 
[d1,d2,d3] = size(I); 
if(d3 > 1) 
I = rgb2gray(I);
end
I = im2double(I);
[hei,wid,~] = size(I);
subplot(2,2,1),imshow(I);
title('原图像');
% 模拟运动模糊.
LEN = 21;
THETA = 11;
PSF = fspecial('motion', LEN, THETA);%产生运动模糊算子，即点扩展函数
blurred = imfilter(I, PSF, 'conv', 'circular');
subplot(2,2,2), imshow(blurred); title('模糊图像');
Pf = psf2otf(PSF,[hei,wid]);%退化函数的FFT
% 添加加性噪声
noise_mean = 0;
noise_var = 0.00001;
blurred_noisy = imnoise(blurred, 'gaussian',noise_mean, noise_var);
subplot(2,2,3), imshow(blurred_noisy)
title('带运动模糊和噪声图像')
p = [0 -1 0;-1 4 -1;0 -1 0];%拉普拉斯模板
P = psf2otf(p,[hei,wid]);
gama = 0.001;
If = fft2(blurred_noisy);
numerator = conj(Pf);%conj函数，用于求一个复数的复共轭
denominator = Pf.^2 + gama*(P.^2);
deblurred2 = ifft2( numerator.*If./ denominator );%约束最小二乘方滤波在频率域中的表达式
subplot(2,2,4), imshow(deblurred2)
title('约束最小二乘方滤波后图像');

㈡逆滤波、维纳滤波的MATLAB代码

clc; 
clear;
x=rgb2gray(imread('flower2.jpg')); 
x1=x(:,:,1);
x1=double(x1); 
[r,r1]=size(x1); 
y1=fftshift(fft2(x1));
[r,r1]=size(y1); 
figure(1);
imshow(x1,[]);
title('原始的图像') ;
figure(2);
imshow(abs(y1),[0,250000]);
title('原始的图像频谱');
m=1:r; 
m1=1:r1; 
[m,m1]=meshgrid(m,m1);%生成网格空间 
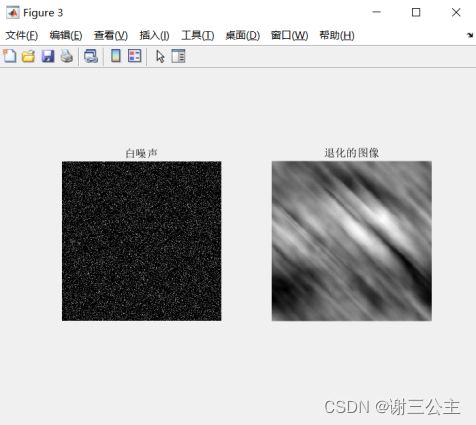
noise=20.*imnoise(zeros(r,r1),'gaussian',0,0.008);%高斯噪声 
figure(3);  
subplot(1,2,1);
imshow(noise,[]);
title('白噪声') ;
a=double(21/100);%x方向的最大移动量为ra的0.21倍,可调 
b=double(21/100);%y方向的最大移动量为ca的0.21倍,可调 
t=double(88/100);%移动到最大所需的时间默认为0.88
f=ones(r,r1);   
g=(m-r/2-1).*a+(m1-r1/2-1).*b+eps;   
f=t.*sin(pi.*g).*exp(-j.*pi.*g)./(pi.*g);
h=f'.*y1; 
tu=ifft2(h);  
tu=abs(tu)+noise; 
subplot(1,2,2);
imshow(tu,[]);
title('退化的图像')%原图傅立叶变换估计值 
y1=h./f'; 
figure(4)
subplot(1,2,1);
imshow(abs(ifft2(y1)),[]);
title('逆滤波的结果');
h=fftshift(fft2(tu));
x=fftshift(fft2(noise));
K=x.*conj(x)./(y1.*conj(y1));%计算K值  
w=(f.*conj(f))'.*h./(f.*(f.*conj(f)+K'))'; 
weina=abs(ifft2(w)); 
subplot(1,2,2);
imshow(weina,[]);
title('维纳滤波的结果');

下面的图给出了第(1)小题的后的图：
代码一运行图：

代码二：
㈠约束最小二乘方滤波对退化图像进行复原图

㈡逆滤波、维纳滤波对退化图像进行复原图

下面是第(2)小题的代码。
（一）选择一幅清晰的灰度图像，对该图像进行仿射变换代码

clear;close all;clc
I=rgb2gray(imread('flower3.jpg'));
figure,imshow(I);
[w,h]=size(I);
theta=pi/4;
t=[100,100];
s=0.5;
%% test affine transform
H_a=projective2d([1 0.5 t(1);
                 0 0.5 t(2);
                 0 0  1]');
newimg=imwarp(I,H_a);
figure,imshow(newimg);

仿射变换后的图：

（二）选择一幅清晰的灰度图像，对该图像进行仿射变换，如然后分别采用连接点选择、空间变换和灰度插值法对几何失真的图像进行复原，比较各种图像复原方法的复原效果，相关代码

clear,clc,close;
Image=im2double(rgb2gray(imread('flower3.jpg')));
[h,w,c]=size(Image);
figure,imshow(Image),title('原图');
RI=imrotate(Image,20);
tform=maketform('affine',[1 0.5 0;0.5 1 0; 0 0 1]);
NewImage=imtransform(RI,tform);
figure,imshow(NewImage),title('几何畸变的图像');
imwrite(NewImage,'GDImage.jpg'); 
cpselect(NewImage,Image);%连接点选择
input_points=[709 577;409 270;320 370];
base_points=[487 305;374 41;134 159];
tform=cp2tform(input_points,base_points,'affine');%空间变换
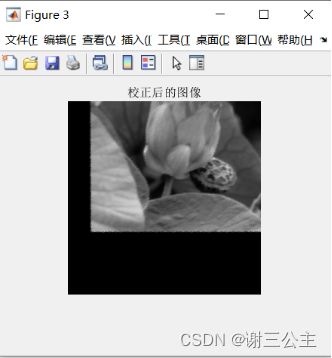
result=imtransform(NewImage,tform,'XData',[1 w],'YData',[1 h]);%灰度插值
figure,imshow(result),title('校正后的图像');
imwrite(result,'jiaozheng.jpg');

复原相关图像：