OpenCV(C++/Python)中的图像对齐(ECC)
OpenCV(C++/Python)中的图像对齐(ECC)

图1 左图:Prokudin Gorskii收藏的图片。右:通道对齐的同一图像
左边的这张照片是名为普罗库丁-戈尔斯基(Prokudin-Gorskii)的历史照片集的一部分。这张照片是一位俄罗斯摄影师在20世纪初用早期的彩色相机拍摄的。由于相机的机械特性,图像的颜色通道未对齐。右侧的图像是同一个图像使用OpenCV 3中提供的功能使通道对齐之后的版本。
OpenCV中的运动模型
在一个典型的图像对齐问题中,我们有一个场景的两幅图像,它们通过一个运动模型相关联。不同的图像对齐算法使用不同的技巧和假设来估计这些运动模型的参数。一旦知道了这些参数,就可以直接对一张图像进行扭曲,使其与另一张图像对齐。让我们快速看看这些运动模型是什么样子的。
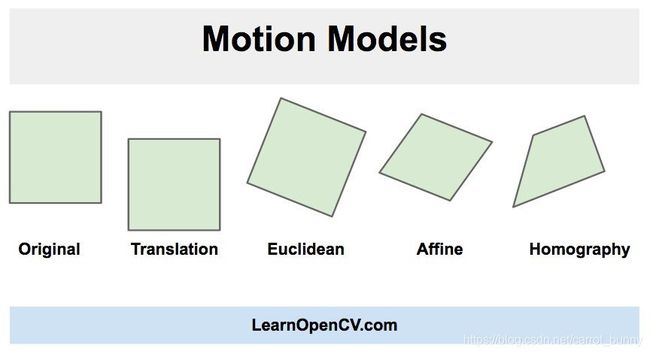 图2 这显示了一个正方形的图像如何通过不同的运动模型进行转换。
图2 这显示了一个正方形的图像如何通过不同的运动模型进行转换。
- Translation ( MOTION_TRANSLATION ):将第一幅图像平移(x, y)得到第二幅图像。我们只需要估算两个参数x和y。
- Euclidean ( MOTION_EUCLIDEAN ) :第一幅图像是第二幅图像的旋转和移位版本。所以有三个参数——x,y和角度。你会注意到在图2中,当一个正方形经过欧几里德(Euclidean)变换时,大小不变,平行线保持平行,直角在变换后保持不变。
- Affine ( MOTION_AFFINE ):仿射变换是旋转、平移、缩放和剪切的组合。该变换有六个参数。当正方形经过仿射变换时,平行线保持平行,但以直角相交的线不再保持正交。
- Homography ( MOTION_HOMOGRAPHY ) :上述所有变换都是2D变换。它们不考虑3D效果。而单应性变换则可以解释一些3D效果(但不是全部)。该转换有8个参数。使用单应变换时,正方形可以变成任何四边形。
在OpenCV中,仿射变换存储在2x3大小的矩阵中。平移变换和欧氏变换是仿射变换的特例。在平移变换中,旋转、缩放和剪切参数为零,而在欧几里得变换中,缩放和剪切参数为零。因此,平移和欧几里得变换也存储在2x3矩阵中。一旦估计出这个矩阵(我们将在下一节中看到),就可以使用warpAffine函数使图像对齐。而单应性变换存储在3 × 3矩阵中。一旦对单应性进行了估计,就可以使用warpPerspective函数对图像进行对齐。
基于增强型相关系数(ECC)最大化的图像配准
OpenCV 3中引入的ECC图像对齐算法基于2008年Georgios D.Evangelidis和Emmanouil Z.Psarakis发表的一篇题为《 Parametric Image Alignment using Enhanced Correlation
Coefficient Maximization》的论文。他们建议使用一种名为增强相关系数(ECC)的新相似性度量来估计运动模型的参数。他们的方法有两个优点。
1. 与传统的像素亮度差异相似性度量不同,ECC在对比度和亮度上不受光度失真的影响。
2. 虽然目标函数是参数的非线性函数,但他们提出的求解优化问题的迭代格式是线性的。换句话说,他们把一个表面上看起来计算成本很高的问题,找到了一种更简单的迭代求解方法。
OpenCV中的findTransformECC示例
在OpenCV 3中,使用函数findTransformECC估计ECC图像对齐的运动模型。以下是使用findTransformECC的步骤
- 读入图片;
- 将它们转换为灰度图像;
- 选择您想要估计的运动模型;
- 分配空间(WARP_MATRIX)存储运动模型;
- 定义一个终止条件,告诉算法何时停止;
- 使用findTransformECC估计扭曲矩阵(warp matrix);
- 将扭曲矩阵(warp matrix)应用于其中一幅图像,使其与另一幅图像对齐。
让我们深入研究代码,看看如何使用它。
C++代码
// Read the images to be aligned
Mat im1 = imread("images/image1.jpg");
Mat im2 = imread("images/image2.jpg");
// Convert images to gray scale;
Mat im1_gray, im2_gray;
cvtColor(im1, im1_gray, CV_BGR2GRAY);
cvtColor(im2, im2_gray, CV_BGR2GRAY);
// Define the motion model
const int warp_mode = MOTION_EUCLIDEAN;
// Set a 2x3 or 3x3 warp matrix depending on the motion model.
Mat warp_matrix;
// Initialize the matrix to identity
if ( warp_mode == MOTION_HOMOGRAPHY )
warp_matrix = Mat::eye(3, 3, CV_32F);
else
warp_matrix = Mat::eye(2, 3, CV_32F);
// Specify the number of iterations.
int number_of_iterations = 5000;
// Specify the threshold of the increment
// in the correlation coefficient between two iterations
double termination_eps = 1e-10;
// Define termination criteria
TermCriteria criteria (TermCriteria::COUNT+TermCriteria::EPS, number_of_iterations, termination_eps);
// Run the ECC algorithm. The results are stored in warp_matrix.
findTransformECC(
im1_gray,
im2_gray,
warp_matrix,
warp_mode,
criteria
);
// Storage for warped image.
Mat im2_aligned;
if (warp_mode != MOTION_HOMOGRAPHY)
// Use warpAffine for Translation, Euclidean and Affine
warpAffine(im2, im2_aligned, warp_matrix, im1.size(), INTER_LINEAR + WARP_INVERSE_MAP);
else
// Use warpPerspective for Homography
warpPerspective (im2, im2_aligned, warp_matrix, im1.size(),INTER_LINEAR + WARP_INVERSE_MAP);
// Show final result
imshow("Image 1", im1);
imshow("Image 2", im2);
imshow("Image 2 Aligned", im2_aligned);
waitKey(0);
重建Prokudin-Gorskii彩色藏品
上图也是普罗库丁-戈尔斯基收藏的一部分。左侧是未对齐RGB通道的图像,右侧是对齐后的图像。这张照片还表明,到了20世纪初,照相底片已经足够灵敏,能够漂亮地捕捉到广泛的彩色光谱。鲜艳的红色、蓝色和绿色令人惊叹。
前一节的代码可以用来解决一个简单的问题。然而,如果你用它来重建上面的图像,你会非常失望。现实世界中的计算机视觉是困难的,事情往往不是真的开箱即用。
问题是,图像中的红色、绿色和蓝色通道在像素强度方面的相关性并不像您可能猜测的那样强。然而,尽管强度不同,但这三个通道中的一些东西是相似的,因为人眼很容易分辨出这是同一个场景。结果表明,图像的三个通道在梯度域中的相关性更强。这并不奇怪,因为尽管三个通道中的强度可能不同,但由对象和颜色边界生成的边缘贴图是一致的。
下面给出图像梯度的近似值
C++代码
using namespace cv;
using namespace std;
Mat GetGradient(Mat src_gray)
{
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
int scale = 1;
int delta = 0;
int ddepth = CV_32FC1; ;
// Calculate the x and y gradients using Sobel operator
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );
// Combine the two gradients
Mat grad;
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
return grad;
}
现在我们准备重建彩色图片!请阅读下面的内联注释
C++代码
using namespace cv;
using namespace std;
// Read 8-bit color image.
// This is an image in which the three channels are
// concatenated vertically.
Mat im = imread("images/emir.jpg", IMREAD_GRAYSCALE);
// Find the width and height of the color image
Size sz = im.size();
int height = sz.height / 3;
int width = sz.width;
// Extract the three channels from the gray scale image
vector<Mat>channels;
channels.push_back(im( Rect(0, 0, width, height)));
channels.push_back(im( Rect(0, height, width, height)));
channels.push_back(im( Rect(0, 2*height, width, height)));
// Merge the three channels into one color image
Mat im_color;
merge(channels,im_color);
// Set space for aligned image.
vector<Mat> aligned_channels;
aligned_channels.push_back(Mat(height, width, CV_8UC1));
aligned_channels.push_back(Mat(height, width, CV_8UC1));
// The blue and green channels will be aligned to the red channel.
// So copy the red channel
aligned_channels.push_back(channels[2].clone());
// Define motion model
const int warp_mode = MOTION_AFFINE;
// Set space for warp matrix.
Mat warp_matrix;
// Set the warp matrix to identity.
if ( warp_mode == MOTION_HOMOGRAPHY )
warp_matrix = Mat::eye(3, 3, CV_32F);
else
warp_matrix = Mat::eye(2, 3, CV_32F);
// Set the stopping criteria for the algorithm.
int number_of_iterations = 5000;
double termination_eps = 1e-10;
TermCriteria criteria(TermCriteria::COUNT+TermCriteria::EPS,
number_of_iterations, termination_eps);
// Warp the blue and green channels to the red channel
for ( int i = 0; i < 2; i++)
{
double cc = findTransformECC (
GetGradient(channels[2]),
GetGradient(channels[i]),
warp_matrix,
warp_mode,
criteria
);
if (warp_mode == MOTION_HOMOGRAPHY)
// Use Perspective warp when the transformation is a Homography
warpPerspective (channels[i], aligned_channels[i], warp_matrix, aligned_channels[0].size(), INTER_LINEAR + WARP_INVERSE_MAP);
else
// Use Affine warp when the transformation is not a Homography
warpAffine(channels[i], aligned_channels[i], warp_matrix, aligned_channels[0].size(), INTER_LINEAR + WARP_INVERSE_MAP);
}
// Merge the three channels
Mat im_aligned;
merge(aligned_channels, im_aligned);
// Show final output
imshow("Color Image", im_color);
imshow("Aligned Image", im_aligned);
waitKey(0);
进一步改进
如果您要真正制作一个商业图像配准产品,您需要做的工作要比我的代码所做的多得多。例如,当不对齐很大时,此代码可能会失败。在这种情况下,需要在较低分辨率版本的图像上估计扭曲参数,并使用在低分辨率版本中估计的参数初始化较高分辨率版本的扭曲矩阵。此外,findTransformECC估计单个全局变换以进行对齐。当图像中存在局部运动(例如,被摄体在两张照片中略有移动)时,该运动模型显然是不合适的。在这种情况下,需要使用例如基于光流的方法进行附加的局部对准。
转载翻译自下面的链接:https://learnopencv.com/image-alignment-ecc-in-opencv-c-python/
(https://learnopencv.com/image-alignment-ecc-in-opencv-c-python/)
