图深度学习——前馈神经网络及训练

前馈神经网络

一个前馈神经网络中叠加了很多神经元

人工神经元

输入是一组向量$x_1,x_2,x_3,x_4$， 参数$w_1,w_2,...,w_4$，参数用于加权求和，通常来说，还会加入偏置$b$。激活函数：引入非线性变换，可以帮助对更复杂事物进行建模。

激活函数

• relu函数，输入为正，那么输入和输出相同，否则输出为0
• sigmoid函数，输出区间(0,1)
• tanh函数，在循环神经网络RNN，LSTM中有应用。

输出层和损失函数

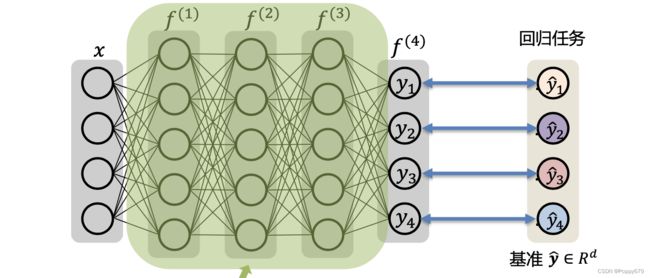
回归任务：ground truth（基准），经过神经网络的预测值去逼近基准值。

损失函数：

$\ell (\mathbf{y},\hat{\mathbf{y}})=\Vert \mathbf{y}-\hat{\mathbf{y}}{\Vert }_2^2$

$\mathcal{L}(\mathbf{W})=\frac{1}{n}{\sum }_{i=1}^n\ell \left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)$

其中，$\ell \left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)$ 表示第 $i$ 个训练样本。

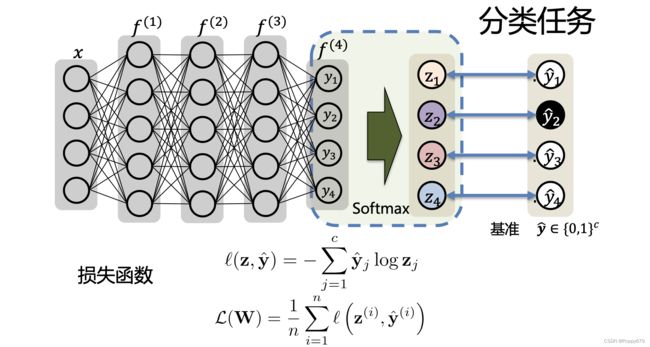
分类任务：基准是一个one-hot编码。对神经网络的输出做一个softmax得到类别的概率，再通过交叉熵损失来衡量预测得到的概率和基准之间的差距。

神经网络的训练

优化目标

${\mathbf{W}}^{\ast }=\arg {\min }_{\mathbf{W}}\mathcal{L}(\mathbf{W})=\frac{1}{n}{\sum }_{i=1}^n\ell \left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)$

最小化损失函数，一般采用梯度下降算法。
梯度下降：梯度方向是函数值上升最快的方向。

${\mathbf{W}}_{n+1}\leftarrow {\mathbf{W}}_n-\eta \nabla \mathcal{L}\left({\mathbf{W}}_n\right)$

这里的 $n$ 是梯度下降的步数。

反向传播

高效计算梯度。如，考虑每一层只有一个神经元的情况

这里的 $w_{(h_0,h_1)}$ 是参数

参数梯度–关于参数的偏导数–使用链式法则

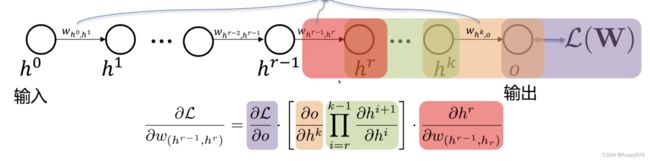
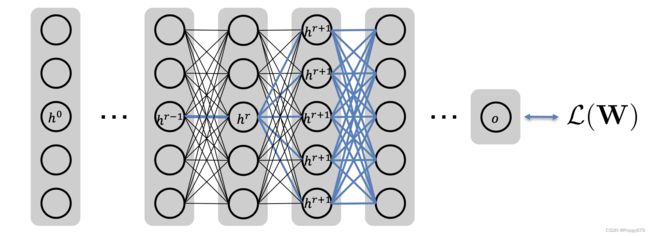
神经网络有很多层，需要计算量很大（指数型增长），所以提出反向传播解决梯度计算问题。

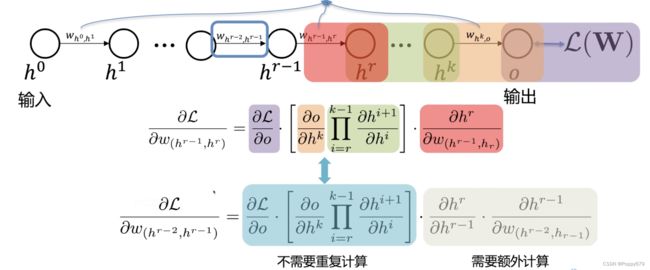
考虑每一层都有多个神经元的情况，相比单个神经元会更复杂，但原理是相似的。