分治算法思想及应用

一. 分治算法介绍

1. 分治算法思想

规模为n的原问题的解无法直接求出，进行问题规模缩减，划分子问题（这里子问题相互独立而且和原问题解的性质是相同的，只是问题规模缩小了）。如果子问题的规模仍然不够小，再进行子问题划分，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止，最后求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原问题的解。

2. 分治算法适用条件

分治算法所能解决的问题一般具有以下几个特征：

• 原问题的规模缩小到一定的程度就可以很容易地解决
• 原问题可以分解为若干个规模较小的相同问题，即原问题具有最优子结构性质
• 利用原问题分解出的子问题的解可以合并为原问题的解
• 原问题分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题（这条特征涉及到分治法的效率，如果各个子问题不独立，也就是子问题划分有重合部分，则分治法要重复的求解1公共子问题的解，此时虽然也可用分治法，但采用动态规划更好）

3. 分治算法的引入

二分查找算法

#include
#include
using namespace std;

bool binarySearch(int arr[], int i, int j, int val)
{
	if (i > j)
		return false;
	int m = (i + j) >> 1;
	if (arr[m] == val)
	{
		return true;
	}
	else if (arr[m] < val)
	{
		return binarySearch(arr, m + 1, j, val);
	}
	else
	{
		return binarySearch(arr, i, m - 1, val);
	}
}
int main()
{
	int arr[] = { 0,5,24,34,41,58,62,64,67,69,78 };
	cout << binarySearch(arr, 0, sizeof(arr) / sizeof(arr[0]), 34) << endl;
}

二. 分治算法的应用

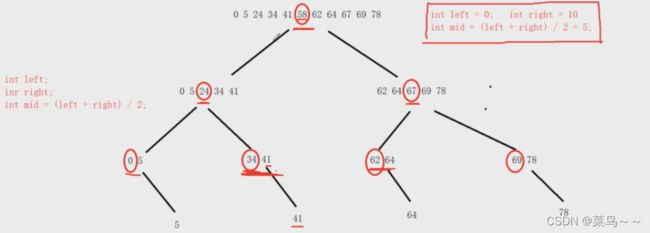
1. 快速排序

对一组数据{41,67,34,0,69,24,78,58,62,64,5}进行快排

#include
#include
using namespace std;

//快排划分函数，调整基准数
int partition(vector<int>& arr, int l, int r)
{
	int val = arr[l];//作为基准数
	while (l < r)
	{
		while (l < r)
		{
			if (arr[r] < val)//右 - 左,找第一个比val小的
			{
				arr[l++] = arr[r];
				break;
			}
			r--;
		}
		while (l < r)
		{
			if (arr[l] > val)//左 - 右，找第一个比val大的
			{
				arr[r--] = arr[l];
				break;
			}
			l++;
		}
	}
	arr[l] = val;//放置基准数
	return l;//返回基准数的下标
}
void quickSort(vector<int>& arr, int l, int r)
{
	if (l >= r)
	{
		return;
	}
	int pos = partition(arr, l, r);
	quickSort(arr, l, pos - 1);
	quickSort(arr, pos + 1, r);
}
int main()
{
	vector<int> arr = { 41,67,34,0,69,24,78,58,62,64,5 };
	quickSort(arr, 0, arr.size() - 1);
	for (int v : arr)
	{
		cout << v << " ";
	}
	cout << endl;
}

2. 快排划分函数求topk问题

求topk问题：

1. 大根堆/小根堆。O(n)线性时间复杂度，利用优先级队列，优先级队列底层一般都是根据大根堆/小根堆设计的，需要借助额外的内存空间，适用于海量数据
2. 快排的划分函数。O(nlogk)线性时间复杂度原地求解，不占用额外的内存空间，但是会修改数组

两种解法各有优缺点，各自适用于不同的场合，因此在动手做题之前要先搞清楚题目要求，包括输入的数据量有多大、能否一次性载入内存、是否允许交换输入数据中数字的顺序

#include
#include
#include
using namespace std;

//快排划分函数，调整基准数
int partition(vector<int>& vec, int l, int r)
{
	int val = vec[l];//作为基准数
	while (l < r)
	{
		while (l < r)
		{
			if (vec[r] < val)//右 - 左,找第一个比val小的
			{
				vec[l++] = vec[r];
				break;
			}
			r--;
		}
		while (l < r)
		{
			if (vec[l] > val)//左 - 右，找第一个比val大的
			{
				vec[r--] = vec[l];
				break;
			}
			l++;
		}
	}
	vec[l] = val;//放置基准数
	return l;//返回基准数的下标
}
//找第k大的，vec.size()-k小的下标
int max_select_topk(vector<int>& vec, int i, int j, int k)
{
	int pos = partition(vec, i, j);
	if (pos == vec.size() - k)//基准数的位置和topk的k值相等
	{
		return pos;
	}
	if (pos > vec.size() - k)//topk应该在基准数左边
	{
		return max_select_topk(vec, i, pos - 1, k);
	}
	else//topk在基准数右边
	{
		return max_select_topk(vec, pos + 1, j, k);
	}
}
//找第k小的，k-1小的下标
int min_select_topk(vector<int>& vec, int i, int j, int k)
{
	int pos = partition(vec, i, j);
	if (pos == k - 1)
	{
		return pos;
	}
	if (pos > k - 1)
	{
		return min_select_topk(vec, i, pos - 1, k);
	}
	else
	{
		return min_select_topk(vec, pos + 1, j, k);
	}
}
int main()
{
	vector<int> vec;
	for (int i = 0; i < 20; i++)
	{
		vec.push_back(rand() % 100);
	}
	//求第top10大的元素
	int pos = max_select_topk(vec, 0, vec.size() - 1,10);
	cout << "第top10大的元素：" << vec[pos] << endl;
	cout << "前top10大的元素为：";
	for (int i = pos; i < vec.size(); i++)
	{
		cout << vec[i] << " ";
	}
	cout << endl;
	pos = min_select_topk(vec, 0, vec.size() - 1, 4);
	cout << "第top4小的元素：" << vec[pos] << endl;
	cout << "前top4小的元素为：";
	for (int i = 0; i <= pos; i++)
	{
		cout << vec[i] << " ";
	}
	cout << endl;
	sort(vec.begin(), vec.end());
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
}

快排的效率和基准数的选择有关，最差是数据已经趋于有序，基准数每次都在边上，二叉树退化为链表，时间复杂度为O(n*n)，所以如果数据已经趋于有序，可以随机一个下标作为基准数

topk问题详解

3. 归并排序

直到划分到子问题只剩一个元素了，认为已经是有序的，然后向上回溯，合并子问题的解

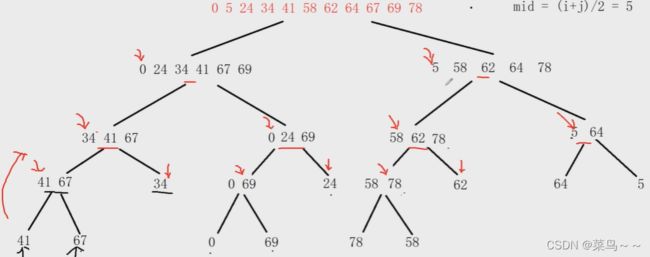
合并出原数组的解需要开辟额外的内存空间，写子问题合并后的解，再额外空间的这些数据找到原数组的范围，不能一边遍历一边写，要不然会把数据覆盖。

归并排序的空间复杂度是O(n)，时间复杂度是O(nlogn)

#include
#include
#include
using namespace std;

void merge(vector<int>& vec, int low, int mid, int high)
{
	//定义额外的辅助空间，存储合并的子问题的有序数组
	vector<int> tmp;
	//不能用resize
	//resize()是分配容器的内存大小，而capacity()只是设置容器容量大小，但并没有真正分配内存
	tmp.reserve(high - low + 1);
	int i = low;//[low,mid]
	int j = mid+1;//[mid+1,high]
	while (i <= mid && j <= high)
	{
		vec[i] > vec[j] ? tmp.push_back(vec[j++]) : tmp.push_back(vec[i++]);
	}
	while (i <= mid)
	{
		tmp.push_back(vec[i++]);
	}
	while (j <= high)
	{
		tmp.push_back(vec[j++]);
	}
	//tmp里面的元素->vec当中
	for (int t : tmp)
	{
		vec[low++] = t;
	}
}
void mergeSort(vector<int>& vec, int i, int j)
{
	//子问题划分到一个元素的时候代表子问题的解已知
	if (i == j)
	{
		return;
	}
	int mid = (i + j) / 2;
	//先划分子问题，降低问题规模
	mergeSort(vec, i, mid);
	mergeSort(vec, mid + 1, j);
	//向上回溯，回溯过程中，合并子问题的解
	merge(vec, i, mid, j);
}
int main()
{
	vector<int> vec;
	for (int i = 0; i < 10; i++)
	{
		vec.push_back(rand() % 100);
	}
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;

	mergeSort(vec, 0, vec.size()-1);
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
}

代码中使用额外内存空间，如果使用vector.push_back的话不能用resize，因为resize会分配内存，并默认值为0，而应该用vector.reserve，设置容器容量大小，不分配内存。

4. 合并k个有序单链表

#include
#include
#include
using namespace std;

struct ListNode
{
	int val;
	ListNode* next;
	ListNode(int x):val(x),next(nullptr){}
};
ListNode* init_link(initializer_list<int> list)
{
	ListNode* head = nullptr;
	ListNode* p = nullptr;
	for (int v : list)
	{
		if (head == nullptr)
		{
			head = new ListNode(v);
			p = head;
		}
		else
		{
			p->next = new ListNode(v);
			p = p->next;
		}
	}
	return head;
}
ListNode* mergeTwoLink(ListNode* p1, ListNode* p2)
{
	ListNode* head = nullptr;
	if (p1 == nullptr)
	{
		return p2;
	}
	if (p2 == nullptr)
	{
		return p1;
	}
	if (p1->val > p2->val)
	{
		head = p2;
		p2 = p2->next;
	}
	else
	{
		head = p1;
		p1 = p1->next;
	}
	ListNode* p = head;
	while (p1 != nullptr && p2 != nullptr)
	{
		if (p1->val > p2->val)
		{
			p->next = p2;
			p = p2;
			p2 = p2->next;
		}
		else
		{
			p->next = p1;
			p = p1;
			p1 = p1->next;
		}
	}
	p->next = p1 ? p1 : p2;
	return head;
}
ListNode* mergeLink(vector<ListNode*>& vlink,int i,int j)
{
	if (i >= j)
	{
		return vlink[i];
	}
	int mid = (i + j) / 2;
	ListNode* left = mergeLink(vlink, i, mid);
	ListNode* right = mergeLink(vlink, mid + 1, j);
	return mergeTwoLink(left, right);
}
int main()
{
	ListNode* p1 = init_link({ 1,3,5,7 });
	ListNode* p2 = init_link({ 2,4,6,8 });
	ListNode* p3 = init_link({ 0,9 });
	ListNode* p4 = init_link({ 1,8 });
	vector<ListNode*> vlink;
	vlink.push_back(p1);
	vlink.push_back(p2);
	vlink.push_back(p3);
	vlink.push_back(p4);
	ListNode* p = mergeLink(vlink, 0, vlink.size() - 1);
	for (ListNode* c = p; c != nullptr; c = c->next)
	{
		cout << c->val << " ";
	}
	cout << endl;
}

5. 对数时间求中位数算法思想

偶数个数升序序列的中位数：(n/2+n/2+1)/2
奇数个数升序序列的中位数：n/2

问题：有两个升序的数组，长度分别是m和n，求两个数组所有元素的中位数是多少？要求在O(logn)时间内完成

分析：

在两个升序数组中找中位数的话，那么就是找第topk个元素，第k个元素就是最中间的那个数字，第k个元素的值就是max(arr[i-1],brr[j-1])，中位数对应的下标应该是(m+n+1)/2。如果找到k，若总长度是偶数，则中位数为(第k个+第k+1个元素)/2 (第k+1个元素应该是min(arr[i],brr[j]))；若总长度为奇数，则中位数为第k个元素。

所以关键就是如何在对数时间内找到i和j合适的位置：

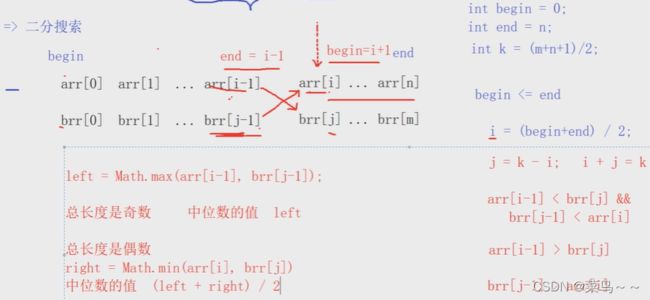
代码实现

#include
#include
#include
#include
using namespace std;

double middleValue(vector<int>& nums1, int length1, vector<int>& nums2, int length2)
{
	//在短的数组中求解合适的i和j值
	if (length1 > length2)
		return middleValue(nums2, length2, nums1, length1);
	if (length1 == 0)
	{
		int k = (length2 - 1) / 2;
		if (length2 - 1 % 2 == 0)
		{
			return (nums2[k] + nums2[k + 1]) * 1.0 / 2;
		}
		else
		{
			return nums2[k];
		}
	}
	int begin = 0;
	int end = length1;
	int k = (length1 + length2 + 1) / 2;
	int i;
	int j;
	//二分搜索的算法思想，在对数时间内找到i+j=k
	while (begin <= end)
	{
		i = (begin + end) / 2;
		j = k - i;
		if (j > 0 && i < length1 && nums2[j - 1] > nums1[i])
		{
			begin = i + 1;
		}
		else if (i > 0 && j<length2 && nums1[i - 1]>nums2[j])
		{
			end = i - 1;
		}
		else
		{
			break;
		}
	}

	int left = 0;
	//nums1特别短，而且nums1数组元素都特别大，中位数肯定在nums2数组中
	if (i == 0)
	{
		left = nums2[j - 1];
	}
	//nums2特别短，中位数肯定都在nums1数组中
	else if (j == 0)
	{
		left = nums1[i - 1];
	}
	else
	{
		left = max(nums1[i - 1], nums2[j - 1]);
	}
	int right = 0;
	//nums1数组元素太小了，而且值都特别小，中位数肯定在nums2数组中
	if (i == length1)
	{
		right = nums2[j];
	}
	//中位数肯定在nums1数组中
	else if (j == length2)
	{
		right = nums1[i];
	}
	else
	{
		right = min(nums1[i], nums2[j]);
	}
	//找到了合适的i和j值
	if ((length1 + length2) % 2 == 0)//偶数长度
	{
		return(left + right) * 1.0 / 2;
	}
	else//奇数长度
	{
		return left;
	}
}
int main()
{
	vector<int> vec1;
	vector<int> vec2;
	for (int i = 0; i < 10; i++)
	{
		vec1.push_back(rand() % 100);
	}
	for (int i = 0; i < 6; i++)
	{
		vec2.push_back(rand() % 100);
	}
	sort(vec1.begin(), vec1.end());
	sort(vec2.begin(), vec2.end());
	vector<int> vec = vec1;
	for (int v : vec2)
	{
		vec.push_back(v);
	}
	sort(vec.begin(), vec.end());
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
	double midval = middleValue(vec1, vec1.size(), vec2, vec2.size());
	cout << midval << endl;
}