tvm学习笔记（八）：卷积操作

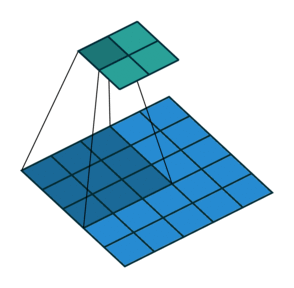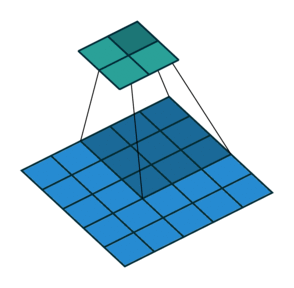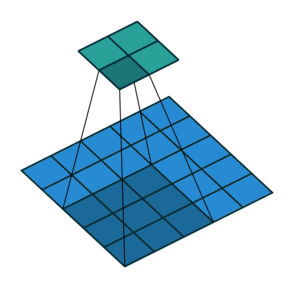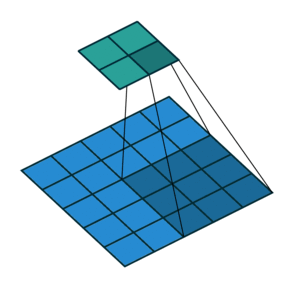
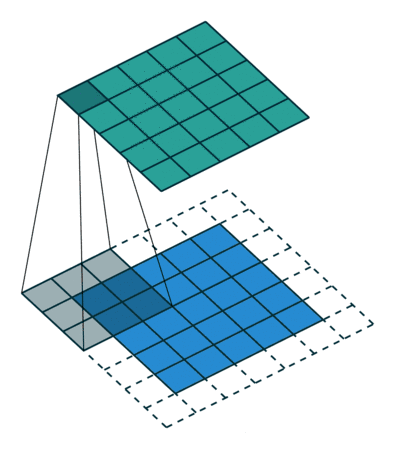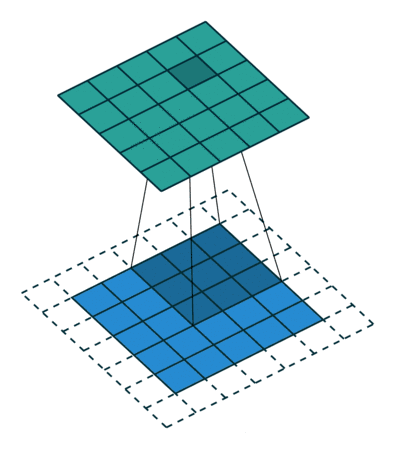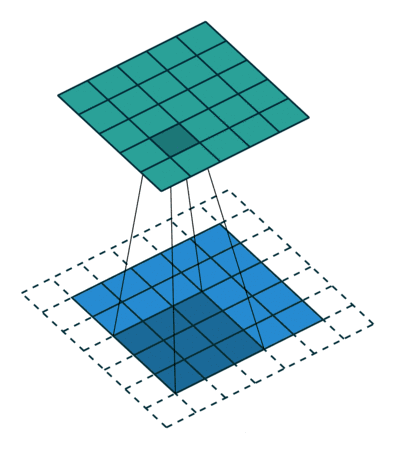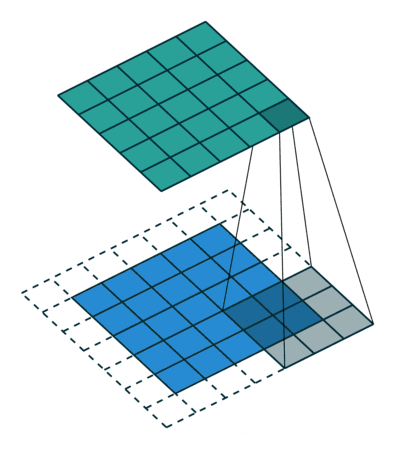
对于卷积神经网络中，卷积操作可能是最常见操作，具体原理可以去学习一下Andred NG的课程，建议搞计算机视觉方向的都去刷一波，具体过程如图1所示：

         

图1 'VALID'方式卷积操作过程

其实就是卷积核与图像待操作区域进行乘加操作，常见的卷积操作有两种形式，第一种是'VALID'的方式，如图1所示，第二种是'SAME'的方式，区别在于'SAME'方式会对输入进行填充，以保证卷积操作之后，输出的size和输入的size一致。

图2 'SAME'方式卷积操作过程

1、padding

先说一下填充padding，padding就是在原始图像四周填充0，对应于图2中虚线部分，使用tvm实现，代码如下：

def padding(X, ph, pw):
    assert len(X.shape) >= 2
    nh, nw = X.shape[-2], X.shape[-1]
    return tvm.compute(
        (*X.shape[0:-2], nh + ph * 2, nw + pw * 2),
        lambda *i: tvm.if_then_else(
            tvm.any(i[-2] < ph, i[-2] >= nh + ph, i[-1] < pw, i[-1] >= nw + pw),
            0, X[i[:-2] + (i[-2] - ph, i[-1] - pw)]
        ), name = 'PaddedX'
    )

2、输出feature map尺寸计算

对于 输入size为n， 卷积核size为k， 填充size为p，卷积操作步长size为s，输出大小为：

对应代码如下：

def conv_out_size(n, k, p, s):
    return (n - k + 2 * p) // s + 1

3、卷积操作

就是将卷积核与要操作的图像块进行乘加操作，对应于tvm代码为：

def conv(oc, ic, nh, nw, kh, kw, ph=0, pw=0, sh=1, sw=1):
    # reduction axes
    ric = tvm.reduce_axis((0, ic), name='ric')
    rkh = tvm.reduce_axis((0, kh), name='rkh')
    rkw = tvm.reduce_axis((0, kw), name='rkw')

    # output height and width
    oh = conv_out_size(nh, kh, ph, sh)
    ow = conv_out_size(nw, kw, pw, sw)

    # pad x and then conpute y
    X = tvm.placeholder((ic, nh, nw), name='x')
    K = tvm.placeholder((oc, ic, kh, kw), name='k')
    # 对输入填充
    PaddedX = padding(X, ph, pw) if ph * pw != 0 else X
    Y = tvm.compute(
        (oc, oh, ow),
        lambda c, i, j: tvm.sum(
            PaddedX[ric, i * sh + rkh, j * sw + rkw] * K[c, ric, rkh, rkw],
            axis=[ric, rkh, rkw]
        ), name='Y'
    )

    return X, K, Y, PaddedX

最后，看一下实际生成的伪代码：

import tvm
import numpy as np
import mxnet as mx

def padding(X, ph, pw):
    assert len(X.shape) >= 2
    nh, nw = X.shape[-2], X.shape[-1]
    return tvm.compute(
        (*X.shape[0:-2], nh + ph * 2, nw + pw * 2),
        lambda *i: tvm.if_then_else(
            tvm.any(i[-2] < ph, i[-2] >= nh + ph, i[-1] < pw, i[-1] >= nw + pw),
            0, X[i[:-2] + (i[-2] - ph, i[-1] - pw)]
        ), name = 'PaddedX'
    )

# 输入size：n
# 卷积核size：k
# 填充size：p
# 步长size：s
def conv_out_size(n, k, p, s):
    return (n - k + 2 * p) // s + 1

def conv(oc, ic, nh, nw, kh, kw, ph=0, pw=0, sh=1, sw=1):
    # reduction axes
    ric = tvm.reduce_axis((0, ic), name='ric')
    rkh = tvm.reduce_axis((0, kh), name='rkh')
    rkw = tvm.reduce_axis((0, kw), name='rkw')

    # output height and width
    oh = conv_out_size(nh, kh, ph, sh)
    ow = conv_out_size(nw, kw, pw, sw)

    # pad x and then conpute y
    X = tvm.placeholder((ic, nh, nw), name='x')
    K = tvm.placeholder((oc, ic, kh, kw), name='k')
    # 对输入填充
    PaddedX = padding(X, ph, pw) if ph * pw != 0 else X
    Y = tvm.compute(
        (oc, oh, ow),
        lambda c, i, j: tvm.sum(
            PaddedX[ric, i * sh + rkh, j * sw + rkw] * K[c, ric, rkh, rkw],
            axis=[ric, rkh, rkw]
        ), name='Y'
    )

    return X, K, Y, PaddedX

def get_conv_data(oc, ic, n, k, p=0, s=1, constructor=None):
    np.random.seed(0)
    data = np.random.normal(size=(ic, n, n)).astype('float32')
    weight = np.random.normal(size=(oc, ic, k, k)).astype('float32')
    on = conv_out_size(n, k, p, s)
    out = np.empty((oc, on, on), dtype='float32')
    if constructor:
        data, weight, out = (constructor(x) for x in [data, weight, out])

    return data, weight, out

oc, ic, n, k, p, s = 4, 6, 12, 3, 1, 1
X, K, Y, _ = conv(oc, ic, n, n, k, k, p, p, s, s)
sch = tvm.create_schedule(Y.op)
mod = tvm.build(sch, [X, K, Y])
print(tvm.lower(sch, [X, K, Y], simple_mode=True))

data, weight, out = get_conv_data(oc, ic, n, k, p, s, tvm.nd.array)
mod(data, weight, out)

def get_conv_data_mxnet(oc, ic, n, k, p, s, ctx='cpu'):
    ctx = getattr(mx, ctx)()
    data, weight, out = get_conv_data(oc, ic, n, k, p, s,
                                      lambda x: mx.nd.array(x, ctx=ctx))
    data, out = data.expand_dims(axis=0), out.expand_dims(axis=0)
    bias = mx.nd.zeros(out.shape[1], ctx=ctx)
    return data, weight, bias, out

def conv_mxnet(data, weight, bias, out, k, p, s):
    mx.nd.Convolution(data, weight, bias, kernel=(k, k), stride=(s, s),
                      pad=(p, p), num_filter=out.shape[1], out=out)
    
data, weight, bias, out_mx = get_conv_data_mxnet(oc, ic, n, k, p, s)
conv_mxnet(data, weight, bias, out_mx, k, p, s)
np.testing.assert_allclose(out_mx[0].asnumpy(), out.asnumpy(), atol=1e-5)

输出为：

// attr [PaddedX] storage_scope = "global"
allocate PaddedX[float32 * 1176]
produce PaddedX {
  for (i0, 0, 6) {
    for (i1, 0, 14) {
      for (i2, 0, 14) {
        PaddedX[(((i0*196) + (i1*14)) + i2)] = tvm_if_then_else(((((i1 < 1) |
| (13 <= i1)) || (i2 < 1)) || (13 <= i2)), 0f, x[((((i0*144) + (i1*12)) + i2) - 13)])      }
    }
  }
}
produce Y {
  for (c, 0, 4) {
    for (i, 0, 12) {
      for (j, 0, 12) {
        Y[(((c*144) + (i*12)) + j)] = 0f
        for (ric, 0, 6) {
          for (rkh, 0, 3) {
            for (rkw, 0, 3) {
              Y[(((c*144) + (i*12)) + j)] = (Y[(((c*144) + (i*12)) + j)] + (P
addedX[(((((ric*196) + (i*14)) + (rkh*14)) + j) + rkw)]*k[((((c*54) + (ric*9)) + (rkh*3)) + rkw)]))            }
          }
        }
      }
    }
  }
}

 

参考资料：

[1] https://blog.csdn.net/kingroc/article/details/88192878

[2] http://tvm.d2l.ai.s3-website-us-west-2.amazonaws.com/