数字地球大气散射的GPU实现
数字地球大气散射的GPU实现
张嘉华 梁成 李桂清
(华南理工大学计算机科学与工程学院 广东 广州 510640)
摘要:本文综合介绍了[Nishita et al 1993]提出的大气散射的物理模型以及[O’Neil 2004, O’Neil 2005]提出的GPU精确大气散射方法,并在此基础上逐步解析了在GPU上实现大气散射效果的原理。在具体实现上,天幕网格建模方面采用了三角片大小一致的构造方式,在GPU上通过若干点的采样实现散射的外积分,通过经验的多项式函数逼近Optical Depth值,代替查找表计算散射的内积分,并给出了在Vertex Shader和Pixel Shader的实现细节。本文将是一篇针对工程人员在实现数字地球的大气散射时好的技术导向文献。
关键词:数字地球、大气散射、GPU、实现细节、顶点程序段、像素程序段
GPU Atmospheric Scattering Of Digital Earth
Zhang Jiahua Liang Cheng Li Guiqing
(College of Computer Science and Engineering, South China University Of Technology , Guangzhou Guangdong, 510640, China)
Abstract This paper synthetically introduces the atmospheric scattering model proposed by [Nishita et al 1993] and accurate GPU atmospheric scattering approaches proposed by [O’Neil 2004, O’Neil 2005]. This paper also explains the theory of atmospheric scattering effect based on GPU step by step. On the implementation, outer atmosphere mesh is modeled by the triangles in the same size. We calculate out-scattering integral by suming at sample points and use experiential multinomial function to approximate Optical Depth value in order to replace lookup table for calculating in-scattering integral. We also give a detail implement about vertex shader and pixel shader. This paper may be a good technologic reference for engineers to implenment atmospheric scattering of digital earth.
Key words Digital Earth, Atmospheric Scattering, GPU, Detail Implement, Vertex Shader, Pixel Shader
引言
大气散射是构成天空颜色的主要因素,也是距离眼睛点很远的对象淡出视野的主要原因。真实感的大气散射效果在场景漫游、飞行模拟等方面都有重要的应用。完全真实地按照大气散射模型进行计算需要很大的计算量,难以实时实现,因此,可以在简化的物理模型上在GPU上加以实时实现。现有的大气散射方法大部分假设大气密度是常数,这可能产生不够真实的效果。
本文实现的程序能够产生视觉上比较逼真的散射效果,并且计算量较少,能够在GPU的Vertex Shader和Pixel Shader无需Shader Model 3.0的情况下实现。本文的主要贡献是详细地解析了[Nishita et al 1993]大气散射模型原理,并探讨了[O’Neil 2004, O’Neil 2005]的GPU实现细节,给工程人员在GPU上实现数字地球大气散射以清晰的思路和细节。
第1节介绍大气散射的相关工作,第2节介绍介绍[Nishita et al 1993]提出的大气散射物理模型及其延伸,第3节介绍了一种三角片大小相等的天幕建模方法,第4节介绍我们在[O’Neil 2004, O’Neil 2005]基础上大气散射效果的GPU细节实现,第5节给出实现的效果。
1 相关工作
大气散射效果的真实感程度与大气散射的物理模型有很大关系,[Nishita et al 1993]提出的大气散射模型认为大气中包含分子和悬浮物质,阳光穿透大气到达视点过程中会产生散射,到达视点的光线密度是光线上所有微粒散射的光线的积分,大气中散射的光线同样能够到达视点,大气的颜色由最终到达视点的光线决定。[Nishita et al 1993]还介绍了从宇宙外和地球内两个不同的角度绘制大气散射效果,随后[Nishita et al 1996,4]介绍了一种快速计算单重大气散射的天空光亮强度分布的方法,并介绍了一种有效计算考虑大气多重散射的天空颜色的方法。[Nishita et al 1996,5s]在[Nishita et al 1993]工作的基础上探讨了大气的各向异性(anisotropic)多重散射,
[O’Neil, 2004]对[Nishita et al 1993]工作进行了简化,在GPU上通过循环采样计算散射的外积分,通过构建一个预生成的查找表来计算散射内积分Optical Depth值。[O’Neil, 2005]用多项式函数逼近来代替查找表计算Optical Depth值,使得每个顶点的散射能够在GPU的Vertex Shader上实现,但是上述方法都没有详细地介绍和解析其实现原理和推导过程,对于普通工程人员实现该方法仍存在一定难度。
2 大气散射的物理模型
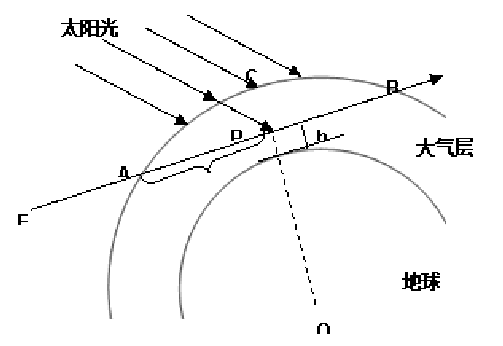
图1:与大气相交的光束强度计算
图1是一次散射的示意图。在P点,入射光线散射到视向路径上(单重散射)。经过一次或多次散射的光线在P点同样朝眼睛点E方向散射。视向和光线方向间夹角θ叫做散射角,该角度是后文提到的散射相位函数的变量。到达眼睛点E的光线总量是沿着整个视向路径上所有散射效果的综合。从P点到达E点前散射光线会收到大气分子的吸收和削弱。
假设大气层密度是连续变化的,大气的颜色主要受太阳光光谱、大气微粒的散射和吸收作用、地表的反射光和太阳与视点位置关系影响。太阳光进入大气层后将会被大气分子和微粒和臭氧层散射和吸收。散射的特征依赖于大气微粒的大小,当散射粒子和波长相比足够少(r<λ/10),例如大气分子等细小粒子,引起的散射叫做Rayleigh散射,散射强度在各个方向是一致的;由悬浮微粒等大粒子(r>λ/10)引起的散射叫做Mie散射,散射强度在各个方向的分布变得复杂,在前向方向上有较多散射能量,两种散射都会削弱光线强度。
如图1,在P点发生散射,那么散射后的光强度IPo有:
其中IPi是P点散射前的入射光强度,h是P点离大气层内边界的高度,λ是P点处光波长,θ是散射角度,G(h, λ, θ)是对Rayleigh散射和Mie散射进行混合的调和函数。为了更好地理解散射物理模型,2.1节和2.2节先介绍Rayleigh散射和Mie散射的物理模型,调和函数G(h, λ, θ)将在2.4节再介绍。
2.1 Rayleigh散射
Rayleigh散射主要由空气中的分子(干净的大气)产生,仅与可见光的散射相关。散射相位系数ωR(θ)(volume angular scattering coefficient),描述了指定波长λ下,在给定方向θ上散射光线的数量,对于Rayleigh散射可以通过公式(2)计算[Irwin 1996]:
其中θ是视向和太阳光方向的夹角,n是大气折射率,N是大气分子密度,λ是入射光波长,FR(θ)是单位化相位函数(normalised phase function),描述散射的方向特征:
Rayleigh 散射的重要性质是1/λ4依赖于波长,短波长光线比长波长的光线更容易散射。短波光线在经过大气时收到非常强烈的削弱,长波光线收到很小影响。这就是为什么白天的时候天空呈现蓝色的原因,而在日落和日出的时候,通过的光线增加,天空的颜色由于短波增多而变红。
散射削弱系数βR(θ)(单位长度的削弱比例)是对公式(2)中ωR(θ)所有角度进行积分导出的,描述了指定波长λ下散射光线的数量:
βR(λ)描述了散射对原入射光线数量的总的削弱程度。
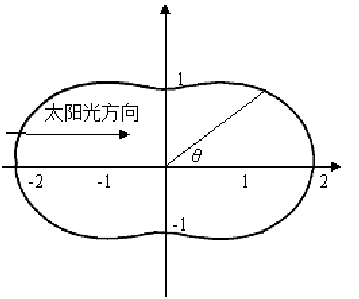
图2:Rayleigh散射相位函数FR(θ),进入视线方向的散射光的强度作为散射角度的函数
大气密度比用ρR (h)表示,高度h为距离大气层内边界的高度,ρR (h)随h变化而变化,可以根据下面公式计算:
其中ρ0取1.00006,H0缩放高度常取值为7994m或8300m。
2.2 Mie散射
Mie散射是一种可以由任意大小粒子产生的散射,从这个角度来说, Rayleigh 散射是Mie散射的一个子集,把Mie散射应用到小粒子上会产生和Rayleigh散射一样的结果。Mie散射相位系数ωM(θ)可以表达如下;
其中c是浓度因子随着混乱T而改变,按如下计算[Preetham et al. 1999]:.
FM(θ,g)是Mie散射相位函数,随着散射粒子大小的改变而改变,可以通过一个著名的相位函数——Henyey-Greenstein函数来近似表达:
其中g是一个不对称因子:
如果g=0,那么公式(8)等价于Rayleigh散射相位公式(2),u由大气条件决定,取值范围由0.7-0.85,因此g取值范围为-0.75至-0.999,g值不能取1或者-1,否则会令公式(8)为0。
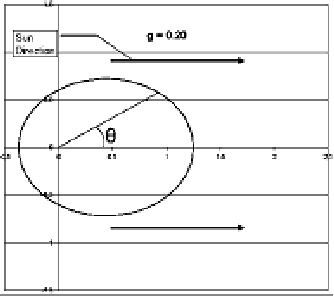
g=0.20
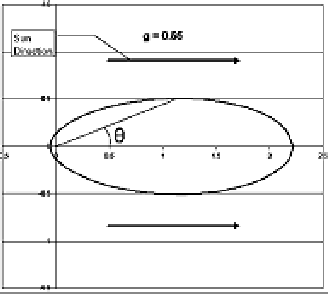
g=0.55
图3:Mie散射相位函数FM(θ,g)
散射削弱系数βM(λ):
其中KM随着波长改变而改变。图4给出了Mie散射函数的图像。
(a) 小粒子Rayleigh散射
(b) 大粒子Mie散射
图4:Mie散射角散射函数
与大气分子的密度分布类似,悬浮微粒的密度分布也与高度呈指数关系,但系数与大气分子不同,H0取1.2Km。
2.3 光学深度(Optical Depth)
在大气光学经常用到光学深度(Optical Depth)这个术语,Optical Depth经常用于光学路径通过指数形式表达散射削弱程度,可以通过散射削弱系数的积分形式表达。
其中β(λ)= βR(λ)+ βM(λ),是Mie散射削弱系数和Rayleigh散射削弱系数之和,ρ (h)随高度h改变,而h与路径l上的某段元路径dl的位置P有关,是变元。这里Optical Depth值t表示波长为λ,通过距离为l的光线受大气分子的削弱程度,可以认为是一个权重因子描述大气中沿着光束路径上微粒多少的量,它反映了微粒对光线的削弱程度。Optical Depth能够用于直接计算经过一段路径上的光线削弱后光亮量:
根据上述推导,如图1所示,到达视点E的光线是经过沿着B到E路径的大气散射和吸收的余下部分,到达P点的光线已经被P至C之间的大气分子和微粒削弱了,从P点散射的光线在到达E前同样被大气分子和微粒给削弱了。
2.4 视点处散射的总光强度
对于一束光线,随着视点位置不同,到达视点的光强度也不同。到达E的光可以看作是由于大气分子沿着光束和大气的交线AB散射和吸收的剩余部分。大气层C点处的光强度IC(λ)=IS(λ),IS(λ)是大气层顶部入射光的太阳辐射强度,接下来考察在AB上的某一个点P点,P点散射前沿CP方向的入射光强度IPi(λ)可以通过把IC乘以CP段削弱程度量计算得到。通过对公式(11) Optical Depth计算公式中设置CP为积分区间计算得到IPi(λ):
其中t(CP, λ)是从大气层顶部到P点的Optical Depth,t(CP, λ)的计算公式如下:
其中,s是积分变量。在P点发生散射,应用公式(1)计算散射后的P点沿PE方向的光强度IPo,公式(1)中的调和函数G(h, λ, θ)如下计算:
既然光线从P到达E点过程中也受到削弱,那么E点的光强度IE可以通过把P点散射后的光强度IPo乘以PA区间光学削弱程度量计算得到,PA区间光学削弱程度量与公式(14)类似:
(16)
由于地球到太阳的距离可以认为是无限的,因此太阳光可以认为是平衡光,沿着AB每个点的散射角度可以认为是常数。IE反映的是太阳光通过CP在P点散射后沿PA到达E后的光强度,但是太阳光除了在P点散射外,在AB上的任何一点也存在散射,因此,E点的总的光强度IEtotal需要通过对由于大气分子散射光在AB段上发射了散射到达E的所有IE进行积分计算得到:
(17)
3天幕的几何建模
第2节介绍了大气散射的物理模型,大气散射的绘制实体并不一定是大气层,它可能是地表或者云彩,月亮等其他对象,大气散射效果同样作用在这些对象的绘制中,本文只介绍天幕为绘制对象的情况,其它情况可以参考[O’Neil,2004]。常见的建模方法是构造一个用极坐标表示的半径很大的天幕曲面网格来表示天幕。为了简单起见,大气的厚度忽略不计,只对几何建模好的大气天幕上的每一顶点正确计算屏幕投影位置,每一个象素计算散射后的颜色。因此,我们可以把大气层表示为一层与地球同心球面天幕,其离地高度可以取大气层的平均海波高度。
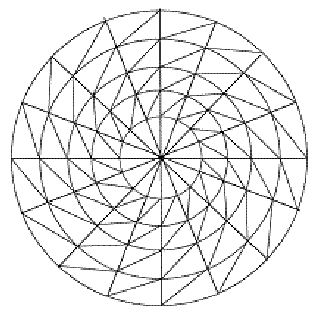
图5:极地地区的经纬度构建的天幕网格
根据绘制的精度不同,通常对这层天幕在极坐标下根据经纬度适当均分构成一个球面网格,采用D3D中的Vertex Buffer和Index Buffer构建(OpenGL中可以采用gluSphere()函数)。如图5,可以相隔若干经度和维度创建一个栅格,但这会导致在极点附近极地区域三角片比较密集,而在赤道地区的三角片很大,因此如果要赤道区域都能很好地用密集的三角片表示,那么需要在极点附近使用非常多的三角片。
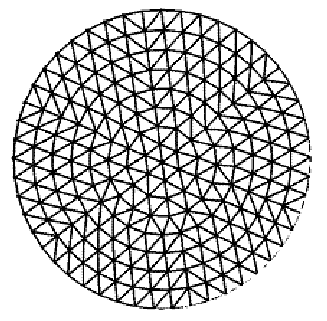
图6:极地地区大小相等三角片构建的天幕网格
为了解决上述问题,因此希望有一种三角片大小相近的组织方法,保持维度带的宽度,并且用相同大小的三角片组织每个维度带。首先把经线带划分为相等大小的片,然后在这些顶点位置创建三角形。有时,这会导致额外的三角片添加和删除依赖于条形带相对于前一个带是展开还是收缩。算法使用一系列条件去决定是否插入一个额外的三角片。
如图1,我们看到的最终大气效果是以E点作为视点观察整个天幕,对于天幕上的每一个顶点,如A、B等将在Vertex Shader计算出其投影在屏幕后的位置,并在Pixel Shdaer根据上述大气散射的物理模型计算出其最终颜色。
4 GPU实现细节
如图7,从视点E到大气层天幕顶点B的光通过大气层,与大气层存在交线AB,那么A点定义为光束通过大气层的起始点,B点定义为光束通过大气层的结束点。假设视点和绘制的网格实体顶点均在大气层外的宇宙空间,那么还需要对光束和大气层进行求交,求出A点和B点。根据上文提到,天幕是以大气层外层作为绘制的几何网格,因此,B点通常就是天幕的顶点,也就是Vertex Shader中输入的顶点,只需要计算A点。
4.1 外积分计算
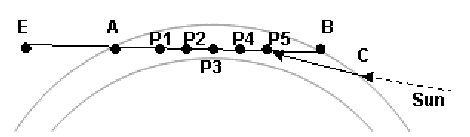
第2节介绍的[Nishita et al 1993]提出的散射模型里存在大量的积分,可以采用梯形法来计算积分,把积分形式转化为循环采样计算后求和,对于某一路径上的积分,采样越多得到的近似积分计算结果约精确,但需要更大的计算量。如图7,对于公式(17)的外积分,为了计算这个外积分值,在从A到B的P1至P5五个点上进行采样计算,首先计算出五个采样点的坐标,可以根据线段AB线性插值得到。考虑到GPU需要Shader Model 3.0以上才支持动态循环上限,因此只采用了P1—P5五个固定点来采样计算积分。公式(5)中的h可以用采样点坐标转换为极坐标的后的半径值R来计算。
图7:大气散射示意
4.2 内积分计算
即使对外积分进行采样计算后,上述的散射模型的计算量仍然是非常大的,主要是公式(11)的Optical Depth的内积分计算,在GPU实现将会非常慢。为了计算沿着一条光束路径的近似Optical Depth,可以简单地把该光线路径分解为一系列更小的“采样”路径段(元路径),然后循环遍历这些元路径,求每个元路径β(λ)ρ (h) dl的总和,h取每段元路径dl的中心点Pavg的大气高度havg。光线分解得越小,Optical Depth的积分越精确。
对于公式(17),若内积分也5次采样,外积分5次采样,那么共需要在Vertex Shader中进行5×(5+5)次采样每个顶点,另外由于我们有Rayleigh和Mie两类散射,还要分别计算不同波长下两种散射的颜色通道,每个顶点共需要2×3×5×(5+5)约300次计算。因此,可以考虑构建查找表T来避免公式(17)中的内积分[O’Neil, 2004],查找表存放在一张纹理上,查找表T的横轴是归一化表示的大气高度h,使得x=0代表海平面,x=1代表大气外层天幕半径,纵轴是归一化表示的一束从顶点发出的采样光线的角度θ,y=0.0代表竖直向上,y=1.0代表竖直向下,查找表T的每一个纹素T (x,y)表示了一个大气高度为x沿着y角度的散射的光线,该纹素的R值存放Rayliegh散射的大气密度ρR,近似取exp(-h/H0),纹素的G值存放该位置Rayliegh散射的Optical Depth项tR,B值和A值分别存放Mie散射的大气密度ρM和Optical Depth项tM。查找表T需要预先生产。
在对于一段元路径计算Optical Depth时,会存在不能简单处理的情况。如果摄像机处于宇宙空间中,对于每个采样点,可以简单计算它的高度,从查找表T的G和A通道读出Optical Depth值;如果摄像机处于大气层内,查找表T会出错,由于它存储的Optical Depth值是从一个大气层内的点到大气层顶部,它没有存储一个大气层内的点到另外一个大气层内的点的Optical Depth值。为了解决这个问题,可以建立两个查找表(一个用于采样点,一个用于摄像机点),对查得的两个Optical Depth值作减法运算得到需要的Optical Depth值。另外一个问题是,当一个点在摄像机之上,角度对于摄像机向下,会从查找表T得到错误的值。为了解决这个问题,对于两个查找表均反转光束方向来查找。
查找表T解决了内积分问题,但是仍然需要较长的Vertex Shader来实现,另外在Vertex Shader访问查找表T需要Shader Model 3.0的Vertex Texture Fetch技术支持,因此,希望从数学分析的角度通过观察查找表T,把查找表T转化为一个经验函数来处理。[O’Neil, 2005]介绍了一种近似的多项式逼近方法,根据公式(5),查找表T中的大气密度ρ是高度h的函数,与角度θ无关,那么只需要考察原查找表上x轴高度h,y轴角度θ,以及每一项中的Optical Depth值t之间的关系。假设存在对于Optical Depth的经验函数t(h,θ),首先以高度h为x轴,取值范围从0到1,Optical Depth值为y轴,对于从0到1的各种角度θ分别采样,画出单独的曲线在图上。发现当x从0到1变化时,恰好呈现指数递降。为了更好地比较各个曲线的形状,把这些曲线都进行了归一化,发现这些曲线都近似exp(-4h)。参考公式(5)和公式(11),公式(11) Optical Depth值就是对公式(5)的ρ值积分,归一化后当H0=0.25时就是近似e-4h这条曲线。因此,exp(-4h)可以作为一个公因子提出来,Optical Depth值可以近似看作h的函数,定义如下光学深度系数ξ(h):
接下来分析Optical Depth值与角度θ的关系,以角度θ作为x轴,y轴为角度θ的归一化因子,建立一个新的图像来分析,没有发现合适的曲线可以拟合,再尝试以角度θ为x轴,归一化θ的自然对数为y轴,也没有发现合适的曲线可以拟合,因此只能采用多项式来拟合,构造一个角度θ的余弦为变量的尺度函数Scale(cosθ)。最终Optical Depth可以表示为:
(19)
4.3 Vertex Shader
对于Vertex Shader顶点程序段,首先要计算如图7顶点A和B。由于大气天幕网格的输入顶点就是我们需要的B点,那么我们只需要计算散射开始的A点,那么可以先计算从视点E到顶点B的单位化光束向量![]() ,通过求解光束和大气方程求两者的交点A:
,通过求解光束和大气方程求两者的交点A:
其中O点是地心,也是我们的坐标原点,![]() 是从视点E到地心O向量,
是从视点E到地心O向量,![]() 是从E到B点向量,对
是从E到B点向量,对![]() 进行归一单位化,可以得到光束单位向量。RP是P点极坐标参数化后的半径,RA是地球大气外圈半径,得到|EA|后我们根据向量运算法则可以得到A点的坐标vA:
进行归一单位化,可以得到光束单位向量。RP是P点极坐标参数化后的半径,RA是地球大气外圈半径,得到|EA|后我们根据向量运算法则可以得到A点的坐标vA:
那么B点与A点存在下面的关系:
接着通过点积的形式来计算A点散射角度余弦cosθA:
其中Router是大气层外半径,也就是A点的极坐标半径。A点到O点的向量AO,由于O点是三维空间坐标原点,因此等价于A点坐标vA。接着计算A点的大气高度hA:
其中Rinner是大气层内半径,接着根据公式(5)计算A点的大气密度ρA,接着计算公式(11)中的A点Optical Depth值tA,为什么这个值不能省略,在大气层外边界上时要计算这个值呢,主要是由于大气密度在大气层外边界不完全为0,密度虽然呈指数递减并且在大气层外边界很接近0,但是如果不计算这个值得话会在摄像机进入大气层时颜色上呈现一刹那跳跃感,不平滑过渡。
得到A和B点坐标后我们就可以进行循环采样了,首先通过AB间距除以采样数量计算得到采样间距dsample,接着通过线性插值计算出采样点P1-P5坐标VP。然后,对于每一个采样点P,进行下面具体步骤计算:
1) 根据上面求得的每个P点坐标VP计算极坐标下的半径RP,进而计算大气高度hP
2) 根据公式(5)计算P点的大气密度ρP
3) 计算P点对应公式(18)中的ξ(h)
6) 结合4),5)步骤得到P点的Optical Depth:
(25)
7) 计算得到公式(16)中每个采样点P散射的光线到视点E点的削弱量
其中公式(25)可以从公式(18)结合图1推导得到。完成上述步骤后,把所有采样点散射到视点E的削弱量叠加,得到公式(17)中的积分部分,再乘上公式(17)中的系数部分中的波长λ等值。因为象素要比顶点多得多,因此希望把散射计算尽可能放在Vertex Shader中完成,因此除了与每个象素相关的相位函数值在Pixel Shader才计算以外,需要把公式(17)中可以在Vertex Shader计算的部分计算好。由于最终的颜色是Mie散射颜色和Rayleigh散射颜色叠加的,对于Mie散射和Rayleigh散射是不同的,分别用两个纹理坐标存放公式(17)中用到公式(12)的G(h, λ, θ)中除FM(θ,g)和FR(θ)外其他部分的值,以输出到Pixel Shader。
4.4 Pixel Shader
在Pixel Shader对大气天幕中的每个象素进行Mie散射颜色和Rayleigh散射颜色叠加。那么剩下来就是要计算相位函数,在公式(3)和公式(8)中,由于反复用到![]() ,可以先计算
,可以先计算![]() :
:
其中,![]() 为摄像机到顶点的向量,
为摄像机到顶点的向量,![]() 为太阳光源到顶点的向量,通过对
为太阳光源到顶点的向量,通过对![]() 向量和
向量和![]() 向量的点积来计算cosθ。根据公式(3)可以计算得到Rayleigh相位值FR(θ),根据公式(8)计算得到Mie相位值FM(θ,g),Rayleigh相位函数在0度和180度最亮,在90度最暗,对于90度时,整个天幕显得太暗,之所以与实际亮度有点差距,其主要原因是没有进行多重散射计算。得到相位函数后再乘以Vertex Shader传来的其他部分即得到了Mie散射和Rayleigh散射的颜色,把两种颜色叠加起来即得到最终颜色。
向量的点积来计算cosθ。根据公式(3)可以计算得到Rayleigh相位值FR(θ),根据公式(8)计算得到Mie相位值FM(θ,g),Rayleigh相位函数在0度和180度最亮,在90度最暗,对于90度时,整个天幕显得太暗,之所以与实际亮度有点差距,其主要原因是没有进行多重散射计算。得到相位函数后再乘以Vertex Shader传来的其他部分即得到了Mie散射和Rayleigh散射的颜色,把两种颜色叠加起来即得到最终颜色。
5 结果与讨论
我们在NV 8400M GPU上进行了实现,图8给出了试验的效果图。实验机器GPU NV8400m,内存 2G,实验中开启大气绘制效果时渲染帧数为91关闭大气绘制效果时渲染帧数为132,即每帧消耗约3.413毫秒时间绘制大气散射效果。如图8,图8(a)为从宇宙观察地球时大气散射的效果,图8(b)为北京市上空傍晚的散射景象。图8(c)和(d)为极点地区大气散射效果。另外,我们已经应用把大气散射效果应用在为苏州互动创意有限公司(ICT)所开发的数字地球漫游平台客户端上。
(a)
(b)
(c)
(d)
图8:大气散射效果
参考文献
1. O’Neil S. Real-time Atmospheric Scattering, GammeDev.net, 2004
2. O’Neil S. Accurate Atmospheric Scattering, GPU GEMS2. 2005. 253~267
3. Nishita T, Sirai T, Tadamura K, Nakamae E. Display of The Earth Taking into Account Atmospheric Scattering. Proceedings of ACM SIGGRAPH 1993. 27(4): 175~182
4. Nishita T, Dobashi Y, Kaneda K, Yamashita.H. Display method of the sky color taking into account multiple scattering. Proceedings of Pacific Graphics 1996, 117~132
5. Nishita T, Dobashi Y, Nakamae E. Display of clouds taking into account multiple anisotropic scattering and sky. Proceedings of ACM SIGGRAPH 1996, 30(4):379~386.