【PyTorch笔记】60分钟入门PyTorch——自动求导autograd
torch.autograd
torch.autograd是PyTorch自动求导的工具,求导支撑着神经网络的训练。
文章目录
- torch.autograd
-
- 1. 背景
- 2. 在PyTorch中的应用
- 3. autograd中的求导
-
- autograd如何收集梯度呢?
- 选读:用autograd进行向量计算
- 4. 计算图(Computational Graph)
-
- 从DAG中删除(Exclusion from the DAG)
- 5. 拓展阅读
1. 背景
神经网络(NN)是作用在输入数据上的一系列嵌套函数的集合,这些函数由参数(weights和biases)定义,被存储在PyTorch的tensor中。
训练神经网络的两个步骤
- 前向传播:在前向传播中,NN尽最大努力猜测正确的输出结果。如何猜测呢?将输入数据送入到NN中的每一个函数进行处理。
- 反向传播:在反向传播中,NN根据上一步骤猜测的误差来相应地调整参数。如何调整的?它通过从输出结果向回遍历,收集有关函数参数(梯度)的误差的导数,并使用梯度下降来优化参数。更多的细节可以参照3Blue1Brown的讲解视频。
2. 在PyTorch中的应用
下面看一个示例的训练步骤,从torchvision中加载一个预训练的resnet18
模型。
使用随机数创建tensor去表示一张图片:有3个通道,高和宽均为64,相应的标签也用随机数初始化,形状为(1,1000)。
该示例的工作运行在CPU上,而不是GPU(即使tensor被移动到CUDA上)
import torch,torchvision
model = torchvision.models.resnet18(pretrained=True) # 加载模型
data = torch.rand(1,3,64,64) # 创建输入数据
labels = torch.rand(1,1000) # 随机初始化标签
# 将输入数据通过模型的每一层来进行预测,所谓前向传播
prediction = model(data)
# 用模型预测值和标签计算误差(损失)
loss = (prediction-labels).sum()
# 使用损失,反向传播通过神经网络
# 在误差的tensor上使用.backward(),它会自动计算模型每一个参数的的梯度并存储在参数的.grad属性中
loss.backward()
# 加载优化器:随机梯度下降
optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
# 使用.step()梯度下降,优化器会根据存储在.grad中的梯度值调整每一个参数
optim.step()
以上是训练一个神经网络的步骤,下面是autograd工作的一些细节——可以随意跳过它们
3. autograd中的求导
autograd如何收集梯度呢?
创建两个tensor:a和b,requires_grad=True,这表明autograd会追踪a和b上的每一个操作
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
使用a和b创建另一个张量Q
Q = 3 a 3 − b 2 Q = 3a^3 - b^2 Q=3a3−b2
Q = 3*a**3 - b**2
假设a和b是神经网络的参数,Q是损失,在训练网络时,需要计算损失的参数的梯度
∂ Q ∂ a = 9 a 2 ∂ Q ∂ b = − 2 b \frac{\partial Q}{\partial a} = 9a^2 \\ \frac{\partial Q}{\partial b} = -2b ∂a∂Q=9a2∂b∂Q=−2b
执行Q.backward(),会自动计算这些梯度,同时在相应的tensor.grad
属性中存储。
我们需要在执行Q.backward()时显式传递gradient属性,因为这里的gradient是一个向量,和Q形状相同,它表示Q的梯度
d Q d Q = 1 \frac{dQ}{dQ}=1 dQdQ=1
同样地,可以把Q聚合成标量,然后隐式地反向传播:Q.sum().backward()
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
现在梯度被保存在a.grad和b.grad中
# 检查收集到的梯度是否正确
print(9*a**2 == a.grad)
print(-2*b == b.grad
tensor([True, True])
tensor([True, True])
选读:用autograd进行向量计算
在数学上,如果有一个向量值函数: y ⃗ = f ( x ⃗ ) \vec y = f(\vec x) y=f(x),用 x ⃗ \vec x x表示的梯度 y ⃗ \vec y y是雅克比矩阵(Jacobian matrix) J J J
J = ( ∂ y ∂ x 1 . . . ∂ y ∂ x n ) = ( ∂ y 1 ∂ x 1 . . . ∂ y 1 ∂ x n . . . . . . . ∂ y m ∂ x 1 . . . ∂ y m ∂ x n ) J = (\frac{\partial y}{\partial x_1}...\frac{\partial y}{\partial x_n})= \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & ... & \frac{\partial y_1}{\partial x_n} \\ .&&.\\.&.&.\\.&&.\\ \frac{\partial y_m}{\partial x_1} & ... & \frac{\partial y_m}{\partial x_n} \end{pmatrix} J=(∂x1∂y...∂xn∂y)=⎝ ⎛∂x1∂y1...∂x1∂ym.......∂xn∂y1...∂xn∂ym⎠ ⎞
通常来说,torch.autograd是计算向量雅克比乘积的工具,也就是,给定一个向量 v ⃗ \vec v v,计算乘积 J T ∗ v ⃗ J^T*\vec v JT∗v。如果 v ⃗ \vec v v是标量函数 l = g ( y ⃗ ) l=g(\vec y) l=g(y)的梯度:
v ⃗ = ( ∂ l ∂ y 1 . . . ∂ l ∂ y m ) T \vec v = (\frac{\partial l}{\partial y_1}...\frac{\partial l}{\partial y_m})^T v=(∂y1∂l...∂ym∂l)T
根据链式法则,用 x ⃗ \vec x x来表示 l l l的梯度,即为向量-雅克比矩阵 乘积
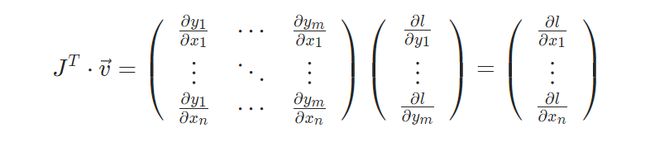
向量雅可比积的这种特性使得将外部梯度馈送到具有非标量输出的模型中非常方便,也是在我们上面的例子中使用的,external_grad代表 v ⃗ \vec v v。
4. 计算图(Computational Graph)
从概念上讲,autograd在由函数对象组成的有向无环图(DAG)中保存数据(tensor)和所有执行的操作(以及由操作产生的新tensor)。在这个DAG中,叶子节点是输入tensors,根节点是输出tensors。从根节点到叶子节点来追踪这个图,可以使用链式法则来自动计算梯度。
在前向传播中,autograd同时做两件事情:
- 运行所请求的操作来计算输出tensor
- 在DAG中保存操作的梯度
当在DAG根节点上调用.backward()时,反向传播开始启动,autograd会做一系列操作:
- 计算每一个
.grad_fn的梯度 - 将它们累加到各自tensor的
.grad属性中 - 使用链式法则,一直传播到叶子节点的tensors
下图是我们示例的DAG可视化表示。在图中,箭头表示前向传播的方向,节点表示在前向传播中的每个操作的向后函数,蓝色的叶子节点表示张量a和b。
DAG在PyTorch中是动态的,在每一次调用.backward()之后,计算图是重新开始创建的,autograd会重新填充一个新的图,这就是允许在模型中使用控制流语句的原因。
可以根据需求在每次迭代时更改形状、大小和操作。
从DAG中删除(Exclusion from the DAG)
如果requires_grad设置为True,torch.autograd就可以追踪对tensor的相关操作。如果不需要tensor的梯度,把属性设置成False就可以从DAG的梯度计算中排除。
即使只有一个简单的输入tensor的requires_grad=True,输出tensors也需要梯度。
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)
a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
Does `a` require gradients? : False
Does `b` require gradients?: True
在一个网络结构中,通常把不需要计算梯度的参数称为冻结参数(frozen parameters)。如果提前知道哪些参数不需要计算梯度,模型的冻结功能非常有用,还可以通过减少梯度计算来提升性能受益。
另一个从DAG中删除的应用是微调一个预训练的模型
在微调的过程中,会冻结模型中的大部分,通常只修改分类层来预测新的标签。让我们通过一个小例子来说明,向以前一样,我们加载预训练模型resnet18,并且冻结所有参数。
from torch import nn,optim
model = torchvision.models.resnet18(pretrained=True)
# 冻结网络中的所有参数
for param in model.parameters():
param.requires_grad = False
"""
目的:在有10个标签的新数据集上微调模型
resnet最后一层的线性分类器为:model.fc
我们可以简单的使用一个新的线性层(默认未冻结)来代替它作为分类器
"""
model.fc = nn.Linear(512,10)
"""
现在除了model.fc的参数,模型的所有参数被冻结了
只有model.fc的weights和bias来参与梯度计算
"""
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
【注意】尽管我们在优化器中注册了所有参数,只有分类器的weights和bias计算梯度并使用梯度下降更新,torch.no_grad()也有同样的功能
5. 拓展阅读
in-place操作&多线程autograd
反向模式autodiff的例子
