双目深度算法——基于Correlation的方法（DispNet / iResNet / AANet）

双目深度算法——基于Correlation的方法（DispNet / iResNet / AANet）

在Stereo Depth算法中一类方法是基于Cost Volume估计视差，这类方法可以参考双目视觉深度——基于Cost Volume的方法（GC-Net / PSM-Net / GA-Net），另外一类就是本文要介绍的介于Correlation的方法，相比于基于Cost Volume的方法，基于Correlation的方法计算量小，但是准确率也相对较低 (最新提出的AANet已经达到了一个较高水平)，下面就这类方法进行一个简单总结：

1. DispNet

DispNet发表于2016年，原论文名为《A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation》，这篇论文的作者和端到端做光流估计的FlowNet的作者是同一人，这篇论文主要也就是印证了类似于FlowNet这样的框架也可以用于进行视差估计，于是作者在FlowNet的基础上做了一些细微改动就得到了DispNet。因此这里我们主要介绍FlowNet的网络结构：

1.1 网络结构

FlowNet的网络结构一共两种类型——FlowNetS和FlowNettC，S指的是Simple的意思，C指的是Correlation的意思，Encoder部分如下图所示：

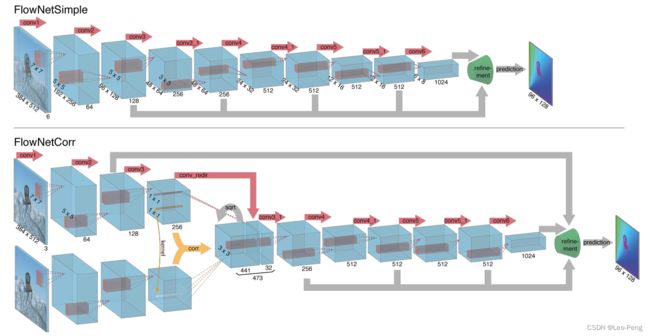
其中FlowNetS是将图片Concat到一起然后经过一系列卷积，FlowNetC则是先用卷积对各个图片进行特征提取，然后用提取的特征进行Correlation，然后再进一步提取特征，这里我们主要关注FlowNetC的结构，中间比较特殊的部分就是Correlation操作（黄色箭头部分），Correlation其实就是分别从两张特征图中各取一个patch进行卷积，具体的计算公式为：$$c\left({\mathbf{x}}_1,{\mathbf{x}}_2\right)=\sum _{\mathbf{o}\in [-k,k]\times [-k,k]}⟨{\mathbf{f}}_1\left({\mathbf{x}}_1+\mathbf{o}\right),{\mathbf{f}}_2\left({\mathbf{x}}_2+\mathbf{o}\right)⟩$$其中$⟨⟩$为卷积符号，${\mathbf{f}}_1$和${\mathbf{f}}_2$分别为进行Correlation的两张特征图，${\mathbf{x}}_1$和${\mathbf{x}}_2$分别为进行Correlation的两个Patch的中心坐标。我们知道，大小为$H\times W\times (2k+1)$的两个Patch卷积后大小为$H\times W\times (2k+1{)}^2$，由于在论文中$k$取的是10，因此在上图中经过Correlation后的特征图的Channel数为$(2\ast 10+1)\times (2\ast 10+1)=441$，在Pytorch的实现里面这一步好像是直接调用了一个CUDA的算子：

import torch
from torch.nn.modules.module import Module
from torch.autograd import Function
import correlation_cuda

class CorrelationFunction(Function):

    @staticmethod
    def forward(ctx, input1, input2, pad_size=3, kernel_size=3, max_displacement=20, stride1=1, stride2=2, corr_multiply=1):
        ctx.save_for_backward(input1, input2)

        ctx.pad_size = pad_size
        ctx.kernel_size = kernel_size
        ctx.max_displacement = max_displacement
        ctx.stride1 = stride1
        ctx.stride2 = stride2
        ctx.corr_multiply = corr_multiply

        with torch.cuda.device_of(input1):
            rbot1 = input1.new()
            rbot2 = input2.new()
            output = input1.new()

            correlation_cuda.forward(input1, input2, rbot1, rbot2, output,
                ctx.pad_size, ctx.kernel_size, ctx.max_displacement, ctx.stride1, ctx.stride2, ctx.corr_multiply)

        return output

    @staticmethod
    def backward(ctx, grad_output):
        input1, input2 = ctx.saved_tensors

        with torch.cuda.device_of(input1):
            rbot1 = input1.new()
            rbot2 = input2.new()

            grad_input1 = input1.new()
            grad_input2 = input2.new()

            correlation_cuda.backward(input1, input2, rbot1, rbot2, grad_output, grad_input1, grad_input2,
                ctx.pad_size, ctx.kernel_size, ctx.max_displacement, ctx.stride1, ctx.stride2, ctx.corr_multiply)

        return grad_input1, grad_input2, None, None, None, None, None, None


class Correlation(Module):
    def __init__(self, pad_size=0, kernel_size=0, max_displacement=0, stride1=1, stride2=2, corr_multiply=1):
        super(Correlation, self).__init__()
        self.pad_size = pad_size
        self.kernel_size = kernel_size
        self.max_displacement = max_displacement
        self.stride1 = stride1
        self.stride2 = stride2
        self.corr_multiply = corr_multiply

    def forward(self, input1, input2):

        result = CorrelationFunction.apply(input1, input2, self.pad_size, self.kernel_size, self.max_displacement, self.stride1, self.stride2, self.corr_multiply)

        return result

在进行Correlation之后，网络还将其中一路的数据进行卷积后Concat到Correlation后的特征图上，也就是图中的conv_redir的操作，我理解这一步应该就是为了保留更多的原始结构的信息，使得输出的光流或者视差更加稳定。FlowNetS和FlowNettC的Decode部分是一致的，结构如下图所示：

在Decoder之后网络不需要做Argmax的操作，而是直接通过L1或者L2损失回归出光流或者视差的大小，网络整体的代码如下图所示：

class FlowNetC(nn.Module):
    def __init__(self,args, batchNorm=True, div_flow = 20):
        super(FlowNetC,self).__init__()

        self.batchNorm = batchNorm
        self.div_flow = div_flow

        self.conv1   = conv(self.batchNorm,   3,   64, kernel_size=7, stride=2)
        self.conv2   = conv(self.batchNorm,  64,  128, kernel_size=5, stride=2)
        self.conv3   = conv(self.batchNorm, 128,  256, kernel_size=5, stride=2)
        self.conv_redir  = conv(self.batchNorm, 256,   32, kernel_size=1, stride=1)

        if args.fp16:
            self.corr = nn.Sequential(
                tofp32(),
                Correlation(pad_size=20, kernel_size=1, max_displacement=20, stride1=1, stride2=2, corr_multiply=1),
                tofp16())
        else:
            self.corr = Correlation(pad_size=20, kernel_size=1, max_displacement=20, stride1=1, stride2=2, corr_multiply=1)

        self.corr_activation = nn.LeakyReLU(0.1,inplace=True)
        self.conv3_1 = conv(self.batchNorm, 473,  256)
        self.conv4   = conv(self.batchNorm, 256,  512, stride=2)
        self.conv4_1 = conv(self.batchNorm, 512,  512)
        self.conv5   = conv(self.batchNorm, 512,  512, stride=2)
        self.conv5_1 = conv(self.batchNorm, 512,  512)
        self.conv6   = conv(self.batchNorm, 512, 1024, stride=2)
        self.conv6_1 = conv(self.batchNorm,1024, 1024)

        self.deconv5 = deconv(1024,512)
        self.deconv4 = deconv(1026,256)
        self.deconv3 = deconv(770,128)
        self.deconv2 = deconv(386,64)

        self.predict_flow6 = predict_flow(1024)
        self.predict_flow5 = predict_flow(1026)
        self.predict_flow4 = predict_flow(770)
        self.predict_flow3 = predict_flow(386)
        self.predict_flow2 = predict_flow(194)

        self.upsampled_flow6_to_5 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=True)
        self.upsampled_flow5_to_4 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=True)
        self.upsampled_flow4_to_3 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=True)
        self.upsampled_flow3_to_2 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=True)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                if m.bias is not None:
                    init.uniform_(m.bias)
                init.xavier_uniform_(m.weight)

            if isinstance(m, nn.ConvTranspose2d):
                if m.bias is not None:
                    init.uniform_(m.bias)
                init.xavier_uniform_(m.weight)
                # init_deconv_bilinear(m.weight)
        self.upsample1 = nn.Upsample(scale_factor=4, mode='bilinear')

    def forward(self, x):
        x1 = x[:,0:3,:,:]
        x2 = x[:,3::,:,:]

        out_conv1a = self.conv1(x1)
        out_conv2a = self.conv2(out_conv1a)
        out_conv3a = self.conv3(out_conv2a)

        # FlownetC bottom input stream
        out_conv1b = self.conv1(x2)
        
        out_conv2b = self.conv2(out_conv1b)
        out_conv3b = self.conv3(out_conv2b)

        # Merge streams
        out_corr = self.corr(out_conv3a, out_conv3b) # False
        out_corr = self.corr_activation(out_corr)

        # Redirect top input stream and concatenate
        out_conv_redir = self.conv_redir(out_conv3a)

        in_conv3_1 = torch.cat((out_conv_redir, out_corr), 1)

        # Merged conv layers
        out_conv3_1 = self.conv3_1(in_conv3_1)

        out_conv4 = self.conv4_1(self.conv4(out_conv3_1))

        out_conv5 = self.conv5_1(self.conv5(out_conv4))
        out_conv6 = self.conv6_1(self.conv6(out_conv5))

        flow6       = self.predict_flow6(out_conv6)
        flow6_up    = self.upsampled_flow6_to_5(flow6)
        out_deconv5 = self.deconv5(out_conv6)

        concat5 = torch.cat((out_conv5,out_deconv5,flow6_up),1)

        flow5       = self.predict_flow5(concat5)
        flow5_up    = self.upsampled_flow5_to_4(flow5)
        out_deconv4 = self.deconv4(concat5)
        concat4 = torch.cat((out_conv4,out_deconv4,flow5_up),1)

        flow4       = self.predict_flow4(concat4)
        flow4_up    = self.upsampled_flow4_to_3(flow4)
        out_deconv3 = self.deconv3(concat4)
        concat3 = torch.cat((out_conv3_1,out_deconv3,flow4_up),1)

        flow3       = self.predict_flow3(concat3)
        flow3_up    = self.upsampled_flow3_to_2(flow3)
        out_deconv2 = self.deconv2(concat3)
        concat2 = torch.cat((out_conv2a,out_deconv2,flow3_up),1)

        flow2 = self.predict_flow2(concat2)

        if self.training:
            return flow2,flow3,flow4,flow5,flow6
        else:
            return flow2,

可以看到，DispNet的结构是非常简单的，与结构同样非常简单的GC-Net相比较，速度相对较快，但是准确率相对较低：

2. iResNet

iResNet发表于CVPR2018，原论文名为《Learning for Disparity Estimation through Feature Constancy》，iResNet其实是在另外一篇名为CRL的论文《Cascade Residual Learning: A Two-stage Convolutional Neural Network for Stereo Matching》上进行的优化，CRL的网络结构如下图所示：

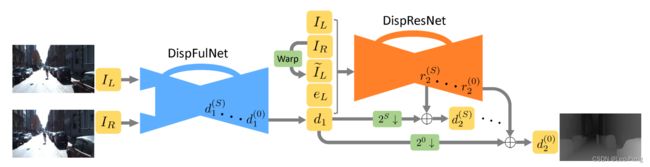
其实就是做两层DispNet，第一层DispNet输出的为初始的视差估计结果，在第二层DispNet的输入为Concat的$I_L,I_R,d_1,{\tilde{I}}_L(x,y)$和$e_L=\left|I_L-{\tilde{I}}_L(x,y)\right|$，输出为基于初始的视差估计结果与最终视差估计结果的残差。从下表的结果可以看出来，加上这样的结构后，相对于原始的DispNet结果由明显提升：

而这里介绍的iResNet则是在，CRL的基础上将第二层DispNet的输入更换成了特征的Concat，使其达到了一个更好的效果：
而且，进化到iResNet这儿，基于Correlation的方法的精度已经超过了GC-Net.

2.1 网络结构

iResNet的网络结构如下：

乍一看iResNet的结构还是有点复杂的，主体仍然是由两层DispNet构成，分别对应着上图中的Disparity Estimation和Disparity Refinment两部分，其中Disparity Estimation部分和原始的DispNet差异不大，下面我们主要来看下Disparity Refinement部分的一些关键点：
（1）使用两种Feature Constancy Term来Refinement初始估计的视差结果，上图中中绿色的部分为初始估计的视差结果，它在Encode的过程中会与着两种两种Feature Constancy Term进行Concat：
第一部分是由多尺度融合特征构成的重建误差，也就是图中的红色部分，也就是根据初始的视差图将右图变换到左图，然后将变换得到的左图与原始的左图计算得到的误差，误差越大的区域值会越大；
第二部分是由浅层特征构成的关联误差，也就是图中的紫色部分，该特征主要表达了一些图像细节部分的关联结果，关联程度越大则值越大；
（2）Disparity Refinement输出的基于初始的视差估计结果与最终视差估计结果的残差，也就是图中的黑色部分，其与原始视差（绿色部分）相加才得到最后的估计的视差结果（黄色部分）
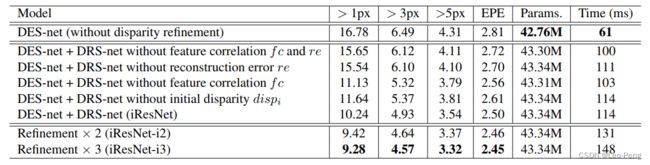
（3）Disparity Refinement模块是可以叠加的，并且不用第一层DispNet，单纯叠加Disparity Refinement模块都是可以的，在论文的消融实验中，Refinement次数越大，估计的准确率越高，如下表所示：

可以看到，iResNet相对于CRL就是将原始输入更换成了原始输入中抽出的一些特征，而正式这些抽出的特征使得模型的灵活性更大，对于噪声的接受程度更高，效果也才会更好。

3. AA-Net

AA-Net发表于CVPR2020，原论文名为《AANet: Adaptive Aggregation Network for Efficient Stereo Matching》，该方法不但在速度上保持了基于Correlation方法的优势，同时准确率上也达到了接近SOTA的水平。

3.1 网络结构

AA-Net网络结构如下图所示：

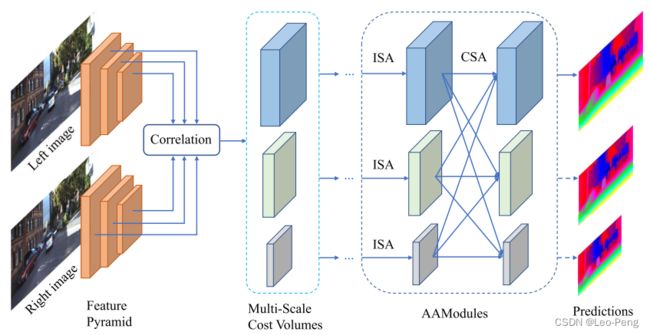
可以看到，AA-Net从整体上也是一个多尺度融合的框架，而框架中最核心的两个模块就是图中标注的ISA和CSA模块，下面我们来分别介绍下这两个模块：
ISA模块指的是Inter-Scale Aggregation，用来代替Local Aggregation模块，在传统视差估计方法中，Local Aggregation方法如下：$$\tilde{\mathbf{C}}(d,\mathbf{p})=\sum _{\mathbf{q}\in N(\mathbf{p})}w(\mathbf{p},\mathbf{q})\mathbf{C}(d,\mathbf{q})$$其中，$\tilde{\mathbf{C}}(d,\mathbf{p})$为像素$\mathbf{p}$处视差大小为$d$的聚合代价，$\mathbf{C}(d,\mathbf{q})$为$\mathbf{q}$处视差大小为$d$的聚合代价，而像素$\mathbf{q}$为像素$\mathbf{p}$周围的像素，$w(\mathbf{p})$为聚合权重，Local Aggregation尽管可以视差不连续的情况，但是同时也会造成边缘和细节出的深度不清晰，在GA-Net中尝试使用卷积自适应学习权重$w(\mathbf{p})$，但是因为聚合的过程仍然是一个固定的大小的卷积，因此对该问题的改善有限，为此AA-Net中就提出了加入可变性卷积来解决这个问题：$$\tilde{C}(d,\mathbf{p})=\sum _{k=1}^{K^2}{w}_k\cdot C\left(d,\mathbf{p}+{\mathbf{p}}_k+\Delta {\mathbf{p}}_k\right)\cdot m_k$$其中，$\tilde{C}(d,\mathbf{p})$仍然是加权后的聚合代价，$K^2$为采样点数量，$w_k$为第$k$个采样点的权重，${\mathbf{p}}_k$为第$k$个采样点的固定偏置，$\Delta {\mathbf{p}}_k$为第$k$个采样点的附加正则化偏置，$m_k$为对权重的调整系数，其中$\Delta {\mathbf{p}}_k$和$m_k$通过单独的卷积层学习获得，整个ISA模块由卷积核大小分别为$1,3,1$的三层卷积构成，卷积核大小为3的中间层为可变形卷积。如下图所示：

采样点（红色）集中在纹理相似的区域，对于右图这种大面积无纹理区域，采样点分布就相对分散，也就保证了在这样的区域，视差不会出现大的图片。而对于左图这种纹理突变的区域，前景的聚合代价就不会收到背景的影响，也就改善了边缘模糊的问题。

CSA模块指的是Cross-Scale Aggregation，本质是一个多尺度融合模块，公式如下：$${\hat{C}}^s=\sum _{k=1}^S{f}_k\left({\tilde{C}}^k\right),s=1,2,\cdots ,S$$其中${\tilde{C}}^k$为经过ISA模块后的聚合代价，${\hat{C}}^s$为警告过CSA模块后的聚合代价，$f_k$为：$$f_k=\{\begin{array}{l}\mathcal{I},k=s\\ (s-k)\text{ stride }-23\times 3\text{ convs, }k<s\\ \text{ upsampling }\oplus 1\times 1\text{ conv, }k>s\end{array}$$其中，$s-k$ stride $-23\times 3$ convs为将分辨率高的聚合代价通过卷积对齐到分辨率的聚合代价，而upsampling $\oplus 1\times 1$ conv指的是通过双线性采样将分辨率较小的聚合代价对齐到分辨率高的聚合代价，最后将对其后的聚合代价相加。这种方法来源于人体检测网络HRNet，可以看到，通过CSA模块，任何分辨率的聚合代价都包含着其他分辨率下的聚合代价信息。

论文中对该两模块的消融实验如下：

可见这两个模块对于网络最后提升都有关键作用。最后在网络训练方法上，AA-Net使用了GA-Net网络的推理结果作为伪真值，激光深度作为真值进行训练以达到更好的结果。