cs224n Assignment 1：exploring_word_vectors

CS224n：Natural Language Processing with DeepLearning

Assignment I

Word Vectors：Introduction，SVD and Word2Vec

---

Abstract

​ Assignment 1 对 Note 1 的内容进行了复现：

• Part I：代码实现 Count-Based 统计方法获得原始 word vectors，而后运用 SVD Decomposition 获得裁剪后的word embedding
• Part II：运用 gensim.downloader 下载预训练数据，并熟悉一些 KeyedVectors对象 对word vector的操作。

Preparation

• 原 jupyter notebook 源文件、本节PPT、本节notes
  • 链接：百度网盘资源，提取码：zdfn
• python 环境中请导入 gensim，确保存在 reuters 数据集（压缩包）
• gensim-data，详情看Part 2

Package

# All Import Statements Defined Here
# Note: Do not add to this list.
# ----------------

import sys
assert sys.version_info[0]==3
assert sys.version_info[1] >= 5

from gensim.models import KeyedVectors
from gensim.test.utils import datapath
import pprint

import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 5]

import nltk
nltk.download('reuters')
from nltk.corpus import reuters

import numpy as np
import random
import scipy as sp

from sklearn.decomposition import TruncatedSVD
from sklearn.decomposition import PCA

START_TOKEN = ''
END_TOKEN = ''

np.random.seed(0)
random.seed(0)
# ----------------

​ 笔者对上述引入的包并不是完全熟悉，所以上网Google了相关资料，下面是对它们的简单介绍：

• Gensim：一款开源的第三方Python工具包，用于从原始的非结构化的文本中无监督地学习到文本隐层的主题向量表达。它支持 TF-IDF、LSA、LDA 和 Word2Vec 在内的多重主题模型算法
• NLTK：全程 natural language toolkit，是一套基于 python 的自然语言处理工具集。nltk包里包含了很多的 corpus，比如 reuters（本作业会用到）、莎士比亚作品、古腾堡语料库等等。
• Reuters（路透社）：关于 news 的语料库，分为“训练”和“测试”两组，便于进行模型训练和测试，命名即为 ‘train/number’ 和 ‘test/number’

---

Part 1：Count-Based Word Vectors

Most word vector models start from the following idea:

· You shall know a word by the company it keeps

  Many word vector implementations are driven by the idea that similar words, i.e., (near) synonyms, will be used in similar contexts. As a result, similar words will often be spoken or written along with a shared subset of words, i.e., contexts. By examining these contexts, we can try to develop embeddings for our words. With this intuition in mind, many “old school” approaches to constructing word vectors relied on word counts. Here we elaborate upon one of those strategies, co-occurrence matrices (for more information, see here or here).

Co-Occurrence

  下面对共生矩阵(co-occurrence matrix)进行简单的介绍。

  对于 document 中的单词 $w_i$，我们给定参数 $window\_sizen$，找出 $w_i$ 对应的窗口内的 context，范围为 $w_{i-n},...,w_{i-1}$ & $w_{i+1},...,w_{i+n}$。针对所有的 document，以及 document 中的所有 $w_i$，我们将计算单词 $w_j$ 出现在 $w_i$ 的 context 中的次数，对应共生矩阵 $M$ 的 $M_{ij}$。

Example: Co-Occurrence with Fixed Window of n=1:

​ Document 1: “all that glitters is not gold”

​ Document 2: “all is well that ends well”

		all	that	glitters	is	not	gold	well	ends
	0	2	0	0	0	0	0	0	0	0
all	2	0	1	0	1	0	0	0	0	0
that	0	1	0	1	0	0	0	1	1	0
glitters	0	0	1	0	1	0	0	0	0	0
is	0	1	0	1	0	1	0	1	0	0
not	0	0	0	0	1	0	1	0	0	0
gold	0	0	0	0	0	1	0	0	0	1
well	0	0	1	0	1	0	0	0	1	1
ends	0	0	1	0	0	0	0	1	0	0
	0	0	0	0	0	0	1	1	0	0

  不难看出，共生矩阵是对称矩阵，且在这里，每个 document 的起始都加上了 START & END标识符。之后将动手实现共生矩阵。

SVD

  SVD（Singular Value Decomposition，奇异值分解），是机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解还可以用于推荐系统，以及自然语言处理等领域，是很多机器学习算法的基石。

  在这里，我们实现了共生矩阵之后，会对其进行降维处理，运用的便是SVD Decomposition，下面的链接整理了SVD分解的相关数学知识。

• SVD分解

Plotting Co-Occurrence Word Embedding

  开始代码操作~

  我们先从 Reuters 中读取文本语料，这个语料库包括了 10,788 条新闻 documents 共 1.3million 个单词。在本节中，我们只用到其中的一些category（所有的documents分了90类）。如上对共生矩阵举例的时候列出的矩阵所示，我们会在 document 起始加上 START & END 标识符，并且把所有的单词转换为小写形式。

  注意：documents 不是我们经常翻译为的文档，在这里，它表示一则新闻或者是一句话。

def read_corpus(category="crude"):
    files = reuters.fileids(category)
    
    return [[START_TOKEN] + [w.lower() for w in list(reuters.words(f))] + [END_TOKEN] for f in files]

1. 读取的 category 主题为 “crude”.

2. 如果对 files 进行循环，实际输出的是迭代器；调用 list(reuters.words()) 方法进一步获得具体的 document（列出部分打印结果）.

3. return 语句中实际上分为了三部分，第一部分加上 START 标识符，第二部分将所有单词变成小写，第三部分则是加上 END 标识符，而最后的 for f in files 语句可以看成最外层的循环，同时也可以注意到，这三个部分都加了 [].

Question 1.1：Implement distinct_words

  对读取到的语料进行去重并排序，得到最终的 corpus 单词列表。In particular, this may be useful to flatten a list of lists. If you’re not familiar with Python list comprehensions in general, here’s more information.（列表解析）

• Params：
  • corpus：list of list of strings，关于 document 的列表，而 document 是关于 word 的列表
• Return：
  • corpus_words：去重并排序的 words list（1-dimension）
  • num_corpus_words：number of words

def distinct_words(corpus):
    corpus_words = []
    num_corpus_words = -1
    
    # ------------------
    # Write your implementation here.
    # 将二维列表平铺
    corpus_words = [word for w in corpus for word in w]
    
    # 去重，利用set集合
    corpus_words = list(set(corpus_words))
    
    # 排序
    corpus_words.sort()
    num_corpus_words = len(corpus_words)

    # ------------------

    return corpus_words, num_corpus_words

• 如何把二维（多维）列表进行平铺，可以着重注意一下

---

测试代码：

# ---------------------
# Run this sanity check
# Note that this not an exhaustive check for correctness.
# ---------------------

# Define toy corpus
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
test_corpus_words, num_corpus_words = distinct_words(test_corpus)

# Correct answers
ans_test_corpus_words = sorted([START_TOKEN, "All", "ends", "that", "gold", "All's", "glitters", "isn't", "well", END_TOKEN])
ans_num_corpus_words = len(ans_test_corpus_words)

# Test correct number of words
assert(num_corpus_words == ans_num_corpus_words), "Incorrect number of distinct words. Correct: {}. Yours: {}".format(ans_num_corpus_words, num_corpus_words)

# Test correct words
assert (test_corpus_words == ans_test_corpus_words), "Incorrect corpus_words.\nCorrect: {}\nYours:   {}".format(str(ans_test_corpus_words), str(test_corpus_words))

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.2：I mplement compute_co_occurrence_matrix

  创建共现矩阵。

• Params：
  • corpus：list of list of strings，未经处理的原始语料
  • window_size：窗口大小
• Return：
  • M：共现矩阵
  • word2ind：dictionary，用处理好（去重并排序）的 words list 创建而成，key 是 word， value 是其在列表中的索引

def compute_co_occurrence_matrix(corpus, window_size=4):
    words, num_words = distinct_words(corpus)
    M = None
    word2ind = {}
    
    # ------------------
    # Write your implementation here.
    M = np.zeros((num_words,num_words))
    
    # 生成索引字典
    word2ind = {c:i for i,c in enumerate(words)}
    
    # 对corpus中所有的记录进行循环
    for document in corpus:
        total = len(document)
        #print(document)
        
        #对单条document中的所有单词进行循环
        for i in range(len(document)):
            curr_word = document[i]
            
            # 找出窗口内的所有单词
            start_index = (i-window_size) if (i-window_size>0) else 0
            end_index = (i+window_size) if (i+window_size<=total) else total
            window_words = document[start_index:i] + document[i+1:end_index+1]

            # 在共生矩阵内+1
            # 这里给自己挖了个坑，共生矩阵关于对角对称，所以第一行代码执行完后，自以为是的保持对称，于是重复加了一遍 1，然而第二行代码并不需要
            for w in window_words:
                M[word2ind[curr_word]][word2ind[w]] += 1
                #M[word2ind[w]][word2ind[curr_word]] += 1   
 
    # ------------------
    
    return M, word2ind

---

测试代码：

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness.
# ---------------------

# Define toy corpus and get student's co-occurrence matrix
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
M_test, word2ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)

# Correct M and word2ind
M_test_ans = np.array( 
    [[0., 0., 0., 0., 0., 0., 1., 0., 0., 1.,],
     [0., 0., 1., 1., 0., 0., 0., 0., 0., 0.,],
     [0., 1., 0., 0., 0., 0., 0., 0., 1., 0.,],
     [0., 1., 0., 0., 0., 0., 0., 0., 0., 1.,],
     [0., 0., 0., 0., 0., 0., 0., 0., 1., 1.,],
     [0., 0., 0., 0., 0., 0., 0., 1., 1., 0.,],
     [1., 0., 0., 0., 0., 0., 0., 1., 0., 0.,],
     [0., 0., 0., 0., 0., 1., 1., 0., 0., 0.,],
     [0., 0., 1., 0., 1., 1., 0., 0., 0., 1.,],
     [1., 0., 0., 1., 1., 0., 0., 0., 1., 0.,]]
)
ans_test_corpus_words = sorted([START_TOKEN, "All", "ends", "that", "gold", "All's", "glitters", "isn't", "well", END_TOKEN])
word2ind_ans = dict(zip(ans_test_corpus_words, range(len(ans_test_corpus_words))))

# Test correct word2ind
assert (word2ind_ans == word2ind_test), "Your word2ind is incorrect:\nCorrect: {}\nYours: {}".format(word2ind_ans, word2ind_test)

# Test correct M shape
assert (M_test.shape == M_test_ans.shape), "M matrix has incorrect shape.\nCorrect: {}\nYours: {}".format(M_test.shape, M_test_ans.shape)

# Test correct M values
for w1 in word2ind_ans.keys():
    idx1 = word2ind_ans[w1]
    for w2 in word2ind_ans.keys():
        idx2 = word2ind_ans[w2]
        student = M_test[idx1, idx2]
        correct = M_test_ans[idx1, idx2]
        if student != correct:
            print("Correct M:")
            print(M_test_ans)
            print("Your M: ")
            print(M_test)
            raise AssertionError("Incorrect count at index ({}, {})=({}, {}) in matrix M. Yours has {} but should have {}.".format(idx1, idx2, w1, w2, student, correct))

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.3：Implement reduce_to_k_dim

  对获得的共生矩阵进行奇异值分解并提取特征。此部分代码参考资料为：sklearn.decomposition.TruncatedSVD

• Params：
  • M：共生矩阵，维度为 (number of unique words in the corpus , number of unique words in the corpus)
  • k：维度裁剪后每个 word 的嵌入维数
• Return：
  • M_reduced：SVD Decomposition 并裁剪之后的单词向量矩阵，维度为 (number of corpus words, k)

def reduce_to_k_dim(M, k=2):
    n_iters = 10     # Use this parameter in your call to `TruncatedSVD`
    M_reduced = None
    print("Running Truncated SVD over %i words..." % (M.shape[0]))
    
    # ------------------
    # Write your implementation here.
    M_reduced = np.zeros((M.shape[0],k))
    svd = TruncatedSVD(n_components = k, n_iter = n_iters)
    M_reduced = svd.fit_transform(M)
    
    #M_reduced = svd.components_.T
    print(M_reduced)
    
    # ------------------

    print("Done.")
    return M_reduced

• TruncatedSVD 方法的源形式为：

class sklearn.decomposition.TruncatedSVD(n_components=2, ***, algorithm=‘randomized’, n_iter=5, random_state=None, tol=0.0)

• fit_transform(X[, y])

Fit model to X and perform dimensionality reduction on X.

---

测试代码：

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness 
# In fact we only check that your M_reduced has the right dimensions.
# ---------------------

# Define toy corpus and run student code
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
M_test, word2ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)
M_test_reduced = reduce_to_k_dim(M_test, k=2)

# Test proper dimensions
assert (M_test_reduced.shape[0] == 10), "M_reduced has {} rows; should have {}".format(M_test_reduced.shape[0], 10)
assert (M_test_reduced.shape[1] == 2), "M_reduced has {} columns; should have {}".format(M_test_reduced.shape[1], 2)

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

Question 1.4：Implement plot_embeddings

Here you will write a function to plot a set of 2D vectors in 2D space.

  可以参考代码 code，其实质为散点图绘制。对于 python 更多的绘图代码，可以参考 the Matplotlib gallery

• Params
  • M_reduced：降维后的单词嵌入矩阵
  • word2ind：words 映射的 dictionary
  • words：需要嵌入的单词 list

def plot_embeddings(M_reduced, word2ind, words):
    # ------------------
    # Write your implementation here.
    for w in words:
        x = M_reduced[word2ind[w]][0]
        y = M_reduced[word2ind[w]][1]
        
        plt.scatter(x,y, marker='x', color='red')
        plt.text(x, y, w, fontsize=9)
    
    plt.show()
    # ------------------

Result：

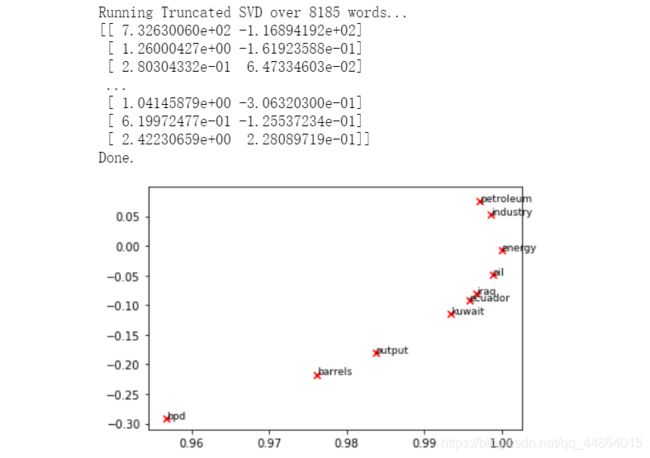
Question 1.5：Co-Occurrence Plot Analysis

  我们将对上面所有实现了的方法进行检验。

TruncatedSVD returns U*S, so we need to normalize the returned vectors, so that all the vectors will appear around the unit circle (therefore closeness is directional closeness).

# -----------------------------
# Run This Cell to Produce Your Plot
# ------------------------------
reuters_corpus = read_corpus()
M_co_occurrence, word2ind_co_occurrence = compute_co_occurrence_matrix(reuters_corpus)
M_reduced_co_occurrence = reduce_to_k_dim(M_co_occurrence, k=2)

# Rescale (normalize) the rows to make them each of unit-length
M_lengths = np.linalg.norm(M_reduced_co_occurrence, axis=1)
M_normalized = M_reduced_co_occurrence / M_lengths[:, np.newaxis] # broadcasting

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']

plot_embeddings(M_normalized, word2ind_co_occurrence, words)

Result：

Part 2：Prediction-Based Word Vectors

​ Research datasets regularly disappear, change over time, become obsolete or come without a sane implementation to handle the data format reading and processing.

  基于这个原因，Gensim 推出了自己的数据集存储，并致力于长期支持一个健全的标准化使用的接口 API、专注于用于非结构化文本处理（没有图像或音频）的数据集。而这个库，便是 gensim-data.

  下面这个 Github 地址给出了这些数据集，并提供了 quick start。同时请注意，若小伙伴们在运行下面的代码出现 bug，并且是因为缺少 information.json 文件，可以将此 repository 中的 list.json 复制到错误提示中 gensim-data 的文件夹下，并更名为 information.json。

  （切忌将代码复制过去自己创建文件，应该把该 repository 下载下来，将 list.json 文件复制过去再更名，否则会出现编码格式不对的问题。）

• https://github.com/RaRe-Technologies/gensim-data

  在本节的作业中，我们使用的是 Glove 预训练模型，同样还存在其他的模型，比如 Word2Vec 等等，具体可以看上面的 Github. OK，回归正题。

def load_embedding_model():
    """ Load GloVe Vectors
        Return:
            wv_from_bin: All 400000 embeddings, each lengh 200
    """
    import gensim.downloader as api
    
    wv_from_bin = api.load("glove-wiki-gigaword-200")
    print("Loaded vocab size %i" % len(wv_from_bin.vocab.keys()))
    
    return wv_from_bin

# -----------------------------------
# Run Cell to Load Word Vectors
# Note: This will take a couple minutes
# -----------------------------------
wv_from_bin = load_embedding_model()

• 日后我们还能利用 gensim.downloader 这个API下载我们想要的数据或模型。
• api.load("glove-wiki-gigaword-200") 这行代码返回的是一个 KeyedVectors 对象
  • 如果打开 glove-wiki-gigaword-200.txt 文件查看，实际上存储的就是 word-word vector，如果不利用 KeyedVectors 对象读取这个文件，则需要一行一行的手动读取。

---

  如果是第一次运行上面的代码特别耗时，所以可以选择手动下载。

• https://github.com/RaRe-Technologies/gensim-data/releases，在这个链接中可以查找想下载的模型，以 glove-wiki-gigaword-200 举例（第一页没找到，可以 next 到下一页）

• 然后找到 Example Code 下方的 Asset

  下载前两项，后两项可自行选择，同时上面给出的百度网盘链接里也有。下载后解压缩到之前存放 information.json 的文件夹下，我的地址是 C:\Users\ACER\gensim-data.

  PS：我重启了电脑再运行上面的代码，下载的好快，人傻了…

  总之下好了就行。继续。

---

Reducing dimensionality of Word Embeddings

  下载下来的词向量有 40,000个，词嵌入维度为 200，数量过多内存占用太大，并且运行起来也很耗时，所以这部分的代码会将 200 维度缩减到 2 维度，并且只取用其中的 10,000 个单词。将构建这 10,000 个单词的嵌入矩阵，也好与Part 1的 co-occurrence matrix 进行比较。

def get_matrix_of_vectors(wv_from_bin, required_vectors=['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']):
    import random
    
    words = list(wv_from_bin.vocab.keys())
    
    print("Shuffle words...")
    random.seed(224)
    random.shuffle(words)
    words = words[:10000]
    
    print("Putting %i words into word2ind and matrix M..." % len(words))
    word2ind = {}
    M = []
    curInd = 0
    
    for w in words:
        try:
            M.append(wv_from_bin.word_vec(w))
            word2ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    
    print("Putting the words in required_vectors but not in words to the M...")
    for w in required_vectors:
        if w in words:
            continue
        try:
            M.append(wv_from_bin.word_vec(w))
            word2ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    
    M = np.stack(M)
    print(M.shape)
    print("Done")
    
    return M,word2ind

• 代码首先将原始的单词序列打散重新排列，然后将其取出其中的 10,000 个，接着创建这 10,000 个单词的词向量矩阵，而后对于不在这 10,000 个单词序列中但却在方法参数 required_words 中的单词添加进矩阵，word2ind类似Part 1
• 如果不了解 np.stack() 方法可参考这篇博文：https://blog.csdn.net/qq_17550379/article/details/78934529，但在这里并没有理解调用 stack() 方法的意义…

Question 2.1: GloVe Plot Analysis

  将 requires_words 中的单词在二维空间中表示出来，结果和利用co-occurrence得到的图像有区别。

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']
plot_embeddings(M_reduced_normalized, word2ind, words)

• 对于单词的集簇情况，除了位置有所改变，什么词和什么词集簇，什么词和什么词没有集簇，大体也和语料的不同有关

Cosine Similarity

Now that we have word vectors, we need a way to quantify the similarity between individual words, according to these vectors.

  实际上为了度量基于词向量的单词之间的相似性，我们除了使用 Cosine similarity，还可以使用 L1 norm和 L2 norm。

​ 计算式：
$$s=\frac{p\cdot q}{||p||||q||},wheres\in -1,1$$

Question 2.2: Words with Multiple Meanings

  很多单词都不止一个意思，这部分可以找出通过余弦相似度来寻找多义词，并且可以列出它表示的最多的 $n$ 个意思。

result = wv_from_bin.most_similar('open')
pprint.pprint(result)

Result：

• 结果与我们五年想象的不一样有可能是因为这里只包含 $10,000$ 个单词，不是corpus的全部

Question 2.3: Synonyms & Antonyms

  当考虑到余弦相似度（Cosine similarity），也常常会考虑到余弦距离（Cosine distance）
$$Cosinedistance=1-Cosinesimilarity$$
  这部分的任务是，找到三个词 $w_1,w_2和w_3$，其中$w_1$和$w_2$是同义词，$w_1$和$w_3$是反义词，并且

$$\begin{gathered} Cosinedistance(w_1,w_2)>Cosinedistance(w_1,w_3) \\ 即Cosinesimilarity(w_1,w_2)<Cosinesimilarity(w_1,w_3) \end{gathered}$$

• 可以想想为什么出现这种情况？
• 也许是因为该语料单词出现在一起的频率不一样，有时候可以尝试一下其他的预训练数据包

w1 = 'hard'
w2 = 'solid'
w3 = 'soft'
    
w1_w2_dist = wv_from_bin.distance('w1','w2')
w1_w3_dist = wv_from_bin.distance('w1','w3')

print(w1_w2_dist)
print(w1_w3_dist)

Question 2.4: Analogies with Word Vectors

  这部分如果上过吴恩达老师的Deep Learning课程的应该不难理解。计算 Cosine similarity 涉及两个单词，那么如果给出 ‘woman’ 和 ‘man’，那么针对于 ‘king’ ，哪个单词（即求$x$）能使下列等式成立：
$$man:king::woman:x$$
  又一次用到 KeyedVectors 对象，并调用它的 most_similar()方法。

result = wv_from_bin.most_similar(positive=['woman','king'],negative=['man'],topn=10)
pprint.pprint(result)

• 参数里面的 10，表示找出最相近的是个单词
• 该方法找出的单词时和 positive list 最相似以及与 $negative$ list最不相近的单词，类比的答案将具有最大的余弦相似度。

Result：

Question 2.5: Finding Analogies

  类似2.4，自己找一个。

pprint.pprint(wv_from_bin.most_similar(positive=['out','white'],negative=['in'],topn=4))

Question 2.6: Incorrect Analogy

  找一个匹配不正确的。

pprint.pprint(wv_from_bin.most_similar(positive=['woman','go'],negative=['man'],topn=4))

  这里不放结果了，自己多试一下，理解个中意思就行。

Question 2.7: Guided Analysis of Bias in Word Vectors

  训练的词向量显然不是完美的，其中的一个需要重视的问题便是偏见的存在，比如性别、种族、性取向等等，如果我们忽视了它的存在，它会通过应用这些模型来强化刻板印象，特别危险。我们通过下面一段代码来看看它的存在;

pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'worker'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['man', 'worker'], negative=['woman']))

Result：

Question 2.8: Independent Analysis of Bias in Word Vectors

  自己找出一个带有bias的例子：

pprint.pprint(wv_from_bin.most_similar(positive=['woman','doctor'],negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['man','doctor'],negative=['woman']))

  看看结果：

• 第一条，man:doctor::woman:? 出现了护士（nurse），而第二条反过来并没有出现，除了人称代词，都是各类医生

小记

• NLTK—co-occurrence matrix
• gensim.downloader
• KeyedVectors