MultiHead-Attention和Masked-Attention的机制和原理
文章目录
- 一、本文说明
- 二. MultiHead Attention
-
- 2.1 MultiHead Attention理论讲解
- 2.2. Pytorch实现MultiHead Attention
- 三. Masked Attention
-
- 3.1 为什么要使用Mask掩码
- 3.2 如何进行mask掩码
- 3.3 为什么是负无穷而不是0
一、本文说明
看本文前,需要先彻底搞懂Self-Attention。推荐看我的另一篇博文层层剖析,让你彻底搞懂Self-Attention、MultiHead-Attention和Masked-Attention的机制和原理。本篇文章内容在上面这篇也有,可以一起看。
二. MultiHead Attention
2.1 MultiHead Attention理论讲解
在Transformer中使用的是MultiHead Attention,其实这玩意和Self Attention区别并不是很大。先明确以下几点,然后再开始讲解:
- MultiHead的head不管有几个,参数量都是一样的。并不是head多,参数就多。
- 当MultiHead的head为1时,并不等价于Self Attetnion,MultiHead Attention和Self Attention是不一样的东西
- MultiHead Attention使用的也是Self Attention的公式
- MultiHead除了 W q , W k , W v W^q, W^k, W^v Wq,Wk,Wv三个矩阵外,还要多额外定义一个 W o W^o Wo。
好了,知道上面几点,我们就可以开始讲解MultiHeadAttention了。
MultiHead Attention大部分逻辑和Self Attention是一致的,是从求出Q,K,V后开始改变的,所以我们就从这里开始讲解。
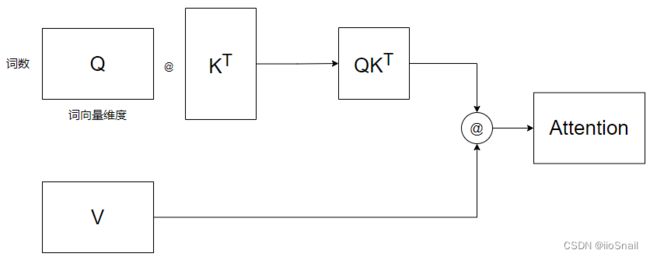
现在我们求出了Q, K, V矩阵,对于Self-Attention,我们已经可以带入公式了,用图像表示则为:
为了简单起见,该图忽略了Softmax和 d k d_k dk 的计算
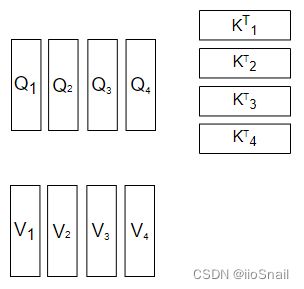
而MultiHead Attention在带入公式前做了一件事情,就是拆,它按照“词向量维度”这个方向,将Q,K,V拆成了多个头,如图所示:
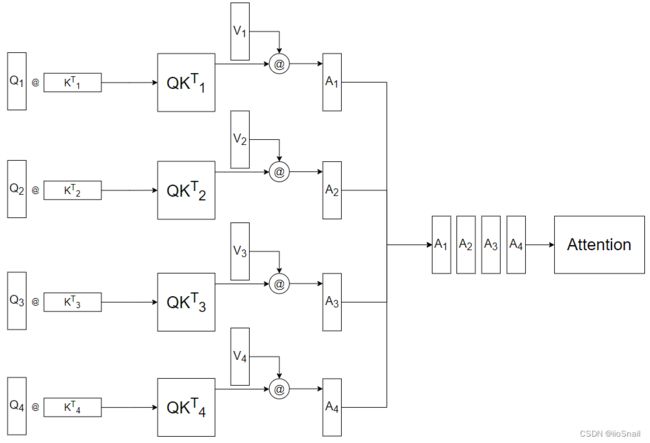
这里我的head数为4。既然拆成了多个head,那么之后的计算,也是各自的head进行计算,如图所示:
但这样拆开来计算的Attention使用Concat进行合并效果并不太好,所以最后需要再采用一个额外的 W o W^o Wo矩阵,对Attention再进行一次线性变换,如图所示:
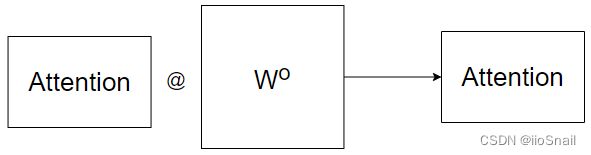
到这里也能看出来,head数并不是越多越好。而为什么要用MultiHead Attention,Transformer给出的解释为:Multi-head attention允许模型共同关注来自不同位置的不同表示子空间的信息。反正就是用了比不用好。
2.2. Pytorch实现MultiHead Attention
该代码参考项目annotated-transformer。
首先定义一个通用的Attention函数:
def attention(query, key, value):
"""
计算Attention的结果。
这里其实传入的是Q,K,V,而Q,K,V的计算是放在模型中的,请参考后续的MultiHeadedAttention类。
这里的Q,K,V有两种Shape,如果是Self-Attention,Shape为(batch, 词数, d_model),
例如(1, 7, 128),即batch_size为1,一句7个单词,每个单词128维
但如果是Multi-Head Attention,则Shape为(batch, head数, 词数,d_model/head数),
例如(1, 8, 7, 16),即Batch_size为1,8个head,一句7个单词,128/8=16。
这样其实也能看出来,所谓的MultiHead其实就是将128拆开了。
在Transformer中,由于使用的是MultiHead Attention,所以Q,K,V的Shape只会是第二种。
"""
# 获取d_model的值。之所以这样可以获取,是因为query和输入的shape相同,
# 若为Self-Attention,则最后一维都是词向量的维度,也就是d_model的值。
# 若为MultiHead Attention,则最后一维是 d_model / h,h为head数
d_k = query.size(-1)
# 执行QK^T / √d_k
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# 执行公式中的Softmax
# 这里的p_attn是一个方阵
# 若是Self Attention,则shape为(batch, 词数, 次数),例如(1, 7, 7)
# 若是MultiHead Attention,则shape为(batch, head数, 词数,词数)
p_attn = scores.softmax(dim=-1)
# 最后再乘以 V。
# 对于Self Attention来说,结果Shape为(batch, 词数, d_model),这也就是最终的结果了。
# 但对于MultiHead Attention来说,结果Shape为(batch, head数, 词数,d_model/head数)
# 而这不是最终结果,后续还要将head合并,变为(batch, 词数, d_model)。不过这是MultiHeadAttention
# 该做的事情。
return torch.matmul(p_attn, value)
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model):
"""
h: head的数量
"""
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
# 定义W^q, W^k, W^v和W^o矩阵。
# 如果你不知道为什么用nn.Linear定义矩阵,可以参考该文章:
# https://blog.csdn.net/zhaohongfei_358/article/details/122797190
self.linears = [
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
]
def forward(self, x):
# 获取Batch Size
nbatches = x.size(0)
"""
1. 求出Q, K, V,这里是求MultiHead的Q,K,V,所以Shape为(batch, head数, 词数,d_model/head数)
1.1 首先,通过定义的W^q,W^k,W^v求出SelfAttention的Q,K,V,此时Q,K,V的Shape为(batch, 词数, d_model)
对应代码为 `linear(x)`
1.2 分成多头,即将Shape由(batch, 词数, d_model)变为(batch, 词数, head数,d_model/head数)。
对应代码为 `view(nbatches, -1, self.h, self.d_k)`
1.3 最终交换“词数”和“head数”这两个维度,将head数放在前面,最终shape变为(batch, head数, 词数,d_model/head数)。
对应代码为 `transpose(1, 2)`
"""
query, key, value = [
linear(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for linear, x in zip(self.linears, (x, x, x))
]
"""
2. 求出Q,K,V后,通过attention函数计算出Attention结果,
这里x的shape为(batch, head数, 词数,d_model/head数)
self.attn的shape为(batch, head数, 词数,词数)
"""
x = attention(
query, key, value
)
"""
3. 将多个head再合并起来,即将x的shape由(batch, head数, 词数,d_model/head数)
再变为 (batch, 词数,d_model)
3.1 首先,交换“head数”和“词数”,这两个维度,结果为(batch, 词数, head数, d_model/head数)
对应代码为:`x.transpose(1, 2).contiguous()`
3.2 然后将“head数”和“d_model/head数”这两个维度合并,结果为(batch, 词数,d_model)
"""
x = (
x.transpose(1, 2)
.contiguous()
.view(nbatches, -1, self.h * self.d_k)
)
# 最终通过W^o矩阵再执行一次线性变换,得到最终结果。
return self.linears[-1](x)
接下来尝试使用一下:
# 定义8个head,词向量维度为512
model = MultiHeadedAttention(8, 512)
# 传入一个batch_size为2, 7个单词,每个单词为512维度
x = torch.rand(2, 7, 512)
# 输出Attention后的结果
print(model(x).size())
输出为:
torch.Size([2, 7, 512])
三. Masked Attention
3.1 为什么要使用Mask掩码
在Transformer中的Decoder中有一个Masked MultiHead Attention。本节来对其进行一个详细的讲解。
首先我们来复习一下Attention的公式:
O n × d v = Attention ( Q n × d k , K n × d k , V n × d v ) = softmax ( Q n × d k K d k × n T d k ) V n × d v = A n × n ′ V n × d v \begin{aligned} O_{n\times d_v} = \text { Attention }(Q_{n\times d_k}, K_{n\times d_k}, V_{n\times d_v})&=\operatorname{softmax}\left(\frac{Q_{n\times d_k} K^{T}_{d_k\times n}}{\sqrt{d_k}}\right) V_{n\times d_v} \\\\ & = A'_{n\times n} V_{n\times d_v} \end{aligned} On×dv= Attention (Qn×dk,Kn×dk,Vn×dv)=softmax(dkQn×dkKdk×nT)Vn×dv=An×n′Vn×dv
其中:
O n × d v = [ o 1 o 2 ⋮ o n ] , A n × n ′ = [ α 1 , 1 ′ α 2 , 1 ′ ⋯ α n , 1 ′ α 1 , 2 ′ α 2 , 2 ′ ⋯ α n , 2 ′ ⋮ ⋮ ⋮ α 1 , n ′ α 2 , n ′ ⋯ α n , n ′ ] , V n × d v = [ v 1 v 2 ⋮ v n ] O_{n\times d_v}= \begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix},~~~~A'_{n\times n} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} & \cdots &\alpha'_{n,1} \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots &\alpha'_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix}, ~~~~V_{n\times d_v}= \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix} On×dv=⎣ ⎡o1o2⋮on⎦ ⎤, An×n′=⎣ ⎡α1,1′α1,2′⋮α1,n′α2,1′α2,2′⋮α2,n′⋯⋯⋯αn,1′αn,2′⋮αn,n′⎦ ⎤, Vn×dv=⎣ ⎡v1v2⋮vn⎦ ⎤
假设 ( v 1 , v 2 , . . . v n ) (v_1, v_2, ... v_n) (v1,v2,...vn) 对应着 ( 机 , 器 , 学 , 习 , 真 , 好 , 玩 ) (机, 器, 学, 习, 真, 好, 玩) (机,器,学,习,真,好,玩)。那么 ( o 1 , o 2 , . . . , o n ) (o_1, o_2, ..., o_n) (o1,o2,...,on) 就对应着 ( 机 ′ , 器 ′ , 学 ′ , 习 ′ , 真 ′ , 好 ′ , 玩 ′ ) (机', 器', 学', 习', 真', 好', 玩') (机′,器′,学′,习′,真′,好′,玩′)。 其中 机 ′ 机' 机′ 包含着 v 1 v_1 v1 到 v n v_n vn 的所有注意力信息。而计算 机 ′ 机' 机′ 时的 ( 机 , 器 , . . . ) (机, 器, ...) (机,器,...) 这些字的权重就是 A ′ A' A′ 的第一行的 ( α 1 , 1 ′ , α 2 , 1 ′ , . . . ) (\alpha'_{1,1}, \alpha'_{2,1}, ...) (α1,1′,α2,1′,...)。
如果上面的回忆起来了,那么接下来看一下Transformer的用法,假设我们是要用Transformer翻译“Machine learning is fun”这句话。
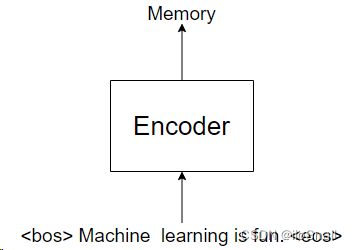
首先,我们会将“Machine learning is fun” 送给Encoder,输出一个名叫Memory的Tensor,如图所示:
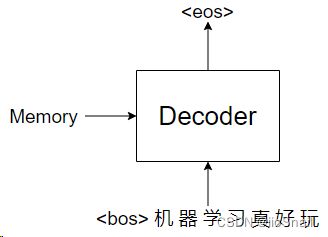
之后我们会将该Memory作为Decoder的一个输入,使用Decoder预测。Decoder并不是一下子就能把“机器学习真好玩”说出来,而是一个词一个词说(或一个字一个字,这取决于你的分词方式),如图所示:
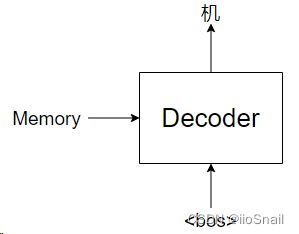
紧接着,我们会再次调用Decoder,这次是传入“
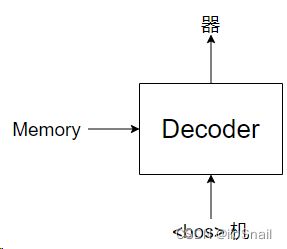
依次类推,直到最后输出
到这里我们就会发现,对于Decoder来说是一个字一个字预测的,所以假设我们Decoder的输入是“机器学习”时,“习”字只能看到前面的“机器学”三个字,所以此时对于“习”字只有“机器学习”四个字的注意力信息。
但是,例如最后一步传的是“
我们不妨来分析一下:
一开始我们只传入了“机”(忽略bos),此时使用attention机制,将“机”字编码为了 [ 0.13 , 0.73 , . . . ] [0.13, 0.73, ...] [0.13,0.73,...]
第二次,我们传入了“机器”,此时使用attention机制,如果我们不将“器”字盖住的话,那“机”字的编码就会发生变化,它就不再是是 [ 0.13 , 0.73 , . . . ] [0.13, 0.73, ...] [0.13,0.73,...]了,也许就变成了 [ 0.95 , 0.81 , . . . ] [0.95, 0.81, ...] [0.95,0.81,...]。
这就会导致第一次“机”字的编码是 [ 0.13 , 0.73 , . . . ] [0.13, 0.73, ...] [0.13,0.73,...],第二次却变成了 [ 0.95 , 0.81 , . . . ] [0.95, 0.81, ...] [0.95,0.81,...],这样就可能会让网络有问题。所以我们为了不让“机”字的编码产生变化,所以我们要使用mask,掩盖住“机”字后面的字,也就是即使他能attention后面的字,也不让他attention。
许多文章的解释是Mask是为了防止Transformer在训练时泄露后面的它不应该看到的信息,我认为这个解释是不对的:①Transformer的Decoder并没有区分训练和测试,所以如果是为了防止训练泄露后面信息的话,那为什么推理时也要掩码呢? ② 传给Decoder的内容都是Decoder自己推理出来的,它自己推理出来的不让它看,说是为了防止泄露信息,这不扯淡嘛。
当然,这也是我的个人看法,也许是我自己理解错看了
3.2 如何进行mask掩码
要进行掩码,只需要对scores动手就行了,也就是 A n × n ′ A'_{n\times n} An×n′ 。直接上例子:
第一次,我们只有 v 1 v_1 v1 变量,所以是:
[ o 1 ] = [ α 1 , 1 ′ ] ⋅ [ v 1 ] \begin{bmatrix} o_1\\ \end{bmatrix}=\begin{bmatrix} \alpha'_{1,1} \end{bmatrix} \cdot \begin{bmatrix} v_1\\ \end{bmatrix} [o1]=[α1,1′]⋅[v1]
第二次,我们有 v 1 , v 2 v_1, v_2 v1,v2 两个变量:
[ o 1 o 2 ] = [ α 1 , 1 ′ α 2 , 1 ′ α 1 , 2 ′ α 2 , 2 ′ ] [ v 1 v 2 ] \begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} [o1o2]=[α1,1′α1,2′α2,1′α2,2′][v1v2]
此时如果我们不对 A 2 × 2 ′ A'_{2\times 2} A2×2′ 进行掩码的话, o 1 o_1 o1的值就会发生变化(第一次是 α 1 , 1 ′ v 1 \alpha'_{1,1}v_1 α1,1′v1,第二次却变成了 α 1 , 1 ′ v 1 + α 2 , 1 ′ v 2 \alpha'_{1,1}v_1+\alpha'_{2,1}v_2 α1,1′v1+α2,1′v2)。那这样看,我们只需要将 α 2 , 1 ′ \alpha'_{2,1} α2,1′ 盖住即可,这样就能保证两次的 o 1 o_1 o1 一致了。
所以第二次实际就为:
[ o 1 o 2 ] = [ α 1 , 1 ′ 0 α 1 , 2 ′ α 2 , 2 ′ ] [ v 1 v 2 ] \begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} [o1o2]=[α1,1′α1,2′0α2,2′][v1v2]
依次类推,如果我们执行到第 n n n次时,就应该变成:
[ o 1 o 2 ⋮ o n ] = [ α 1 , 1 ′ 0 ⋯ 0 α 1 , 2 ′ α 2 , 2 ′ ⋯ 0 ⋮ ⋮ ⋮ α 1 , n ′ α 2 , n ′ ⋯ α n , n ′ ] [ v 1 v 2 ⋮ v n ] \begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 & \cdots & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots & 0 \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix} ⎣ ⎡o1o2⋮on⎦ ⎤=⎣ ⎡α1,1′α1,2′⋮α1,n′0α2,2′⋮α2,n′⋯⋯⋯00⋮αn,n′⎦ ⎤⎣ ⎡v1v2⋮vn⎦ ⎤
3.3 为什么是负无穷而不是0
按照上面的说法,mask掩码是0,但为什么源码中的掩码是 − 1 e 9 -1e9 −1e9 (负无穷)。Attention部分源码如下:
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
你仔细看,我们上面说的 A n × n ′ A'_{n\times n} An×n′ 是什么,是softmax之后的。而源码中呢, 源码是在softmax之前进行掩码,所以才是负无穷,因为将负无穷softmax后就会变成0了。