VFH+避障/局部路径规划算法
VFH+避障/局部路径规划算法
- 1、第一部分:映射到极坐标系
-
-
- VFH+对VFH的改进——考虑机器人的宽度&对障碍物进行膨胀
-
- 2、第二部分:二值化极坐标直方图
-
-
- VFH+算法对此提出了一种解决办法——二值化极坐标直方图
-
- 3、第三部分:限制机器人可选的前进方向
- 4、第四部分:方向选择
做个正直的人
这篇文章是我看论文《VFH+: Reliable Obstacle Avoidance for Fast Mobile Robots》(Iwan Ulrich and Johann Borenstein)的笔记,所以说是文章的翻译也可以。想看原paper的可以自己去找,看过VFH算法的话,这个VFH+算法还是非常好懂的。
我前面写过一篇讲VFH算法的文章,感兴趣的可以去看看。
VFH局部路径规划算法
我在讲VFH算法的最后,写了一点我对VFH算法的评价,主要有两点,一是VFH算法涉及的参数比较多,很麻烦;二是机器人总是会像个傻子一样在原地摆头,我设置了一个不灵敏区域稍微缓解了一下摆头的问题,但是这导致机器人对障碍物的灵敏性降低。
今天看了VFH+算法,才发现原来这些问题前人们早就研究过了。VFH+对VFH提出了几点修正,VFH还带了个正号,这是增强版的意思吗?hhhhhhhh…接下来进入正题。
VFH+算法同样分成四个部分,不过和VFH的四个部分可是不一样。
1、第一部分:映射到极坐标系
VFH算法的第一部分就是把局部地图从笛卡尔空间映射到极坐标系,VFH+算法的做法跟VFH一样,只不过VFH+不再像VFH那样采用正方形的工作空间(可以当成是局部地图),而是采用了圆形的工作空间,本来就该是圆形的好吧,VFH那是为了简便而已。这工作空间一旦变成圆形,就有了一个性质——机器人原地旋转感知到的局部地图是不变的,这称为旋转不变性。
VFH+对VFH的改进——考虑机器人的宽度&对障碍物进行膨胀
VFH并没有考虑机器人的宽度,而是采用一个低通滤波器进行补偿,这个滤波器的参数的设置还比较麻烦。
VFH+考虑到了机器人的宽度 r r r_r rr ,这里假定机器人是正圆盘形状。同时为了安全起见又设置了一个距离障碍物的安全距离 d x d_x dx ,基于此,我们就可以得到需要对障碍区进行膨胀的幅度 r r + x = r r + d x r_{r+x}=r_r+d_x rr+x=rr+dx 。这样我们就可以把机器人完全看做一个点来进行规划,是不是感觉事情变得简单了。
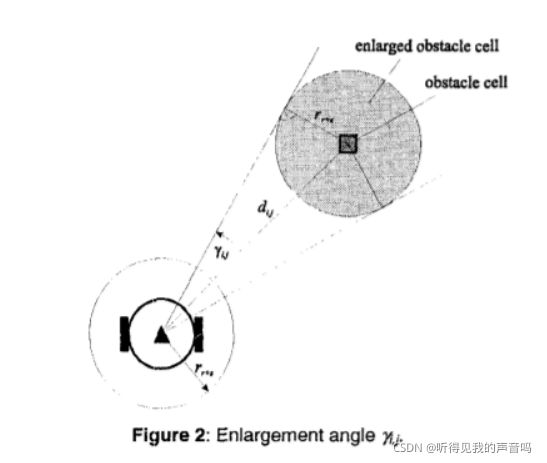
从上图可以看出,如果障起舞膨胀幅度为 r r + x = r r + d x r_{r+x}=r_r+d_x rr+x=rr+dx ,机器人距离障碍物的距离为
d i j d_{ij} dij ,此时这一个障碍物对应的张角为 2 γ i , j 2\gamma_{i,j} 2γi,j 。其中 γ i , j = a r c s i n ( r r + x / d i , j ) \gamma_{i,j}=arcsin(r_{r+x}/d_{i,j}) γi,j=arcsin(rr+x/di,j) 。
此时,这个障碍物很可能就不再仅仅位于一个sector内了,而是同时处于多个sector上,这时候更新工作空间就必须同时对多个sector进行更新。
2、第二部分:二值化极坐标直方图
VFH算法的一个大问题就是机器人会出现在原地频繁的左右摆头的现象,我在调试VFH算法的时候分析是VFH算法对新计算出的前进方向过于敏感,导致机器人频繁的更新自己的前进方向。所以我给VFH算法设置了一个不灵敏区间,只有当新的前进方向和自己当前的前进方向角度相差大于一定阈值的时候才会更新前进的方向,否则不会更新。但是这导致机器人对障碍物的灵敏性降低,限制了机器人的运行速度。
VFH+算法对此提出了一种解决办法——二值化极坐标直方图
VFH算法之所以会出现摆头现象(VFH+算法称之为犹豫不决的行为),是因为在存在一些比较窄(不是真的特别特别窄,只是比较窄而已)的通道的环境中,一些山谷可能会在opening和block的状态之间频繁变换。比如对于一扇开着的门,当离得比较远的时候,这一扇门占据的sector比较窄,而VFH更加倾向于选择那些宽的山谷(占据sector比较多的山谷方向),这时候这一扇门被当作是block,不会成为机器人的候选前进方向;可是随着机器人的运动,机器人离门越来越近,这一扇门占据的sector越来越多,当大于一个阈值的时候,这一扇门突然成了宽的山谷,而成为了候选的前进方向。这就导致一些方向频繁的在opening和block之间跳换,就像一条路,一会跟我说这条路可以走,一会又跟我说不可以走,这不是在拿机器人涮着玩嘛。
VFH+算法的做法是设置两个阈值, τ H i g h \tau_{High} τHigh 和 τ L o w \tau_{Low} τLow ,这样做的目的是降低一些方向在opening和block状态之间跳转的速度,你不是变大了吗(变小也是一样),虽然满足了我的第一个条件,但是我并不马上认可你,而是继续考核你一下,满足我的第二个要求后才是真的合格了,我才会认可你。就是这个思路,在机器人运动过程中,极坐标直方图也在慢慢的发生着变化,有些区域离开了工作空间,有些区域新加入工作空间,并且工作空间内部的物体相对于机器人的位置也在变化,所以会在每一个时刻生成一个极坐标直方图。将n时刻的极坐标直方图中的每一项 H k , n p H_{k,n}^p Hk,np 都和前一时刻对应的项 H k , n − 1 p H_{k,n-1}^p Hk,n−1p 做比较,同时跟设定的两个阈值 τ H i g h \tau_{High} τHigh 和 τ L o w \tau_{Low} τLow 进行比较,依次来决定这一项应该二值化为1还是0,亦或是继续保持前一时刻的值。下面的公式一看就明白了
- H k , n p H_{k,n}^p Hk,np =1 if H k , n p > τ H i g h H_{k,n}^p >\tau_{High} Hk,np>τHigh :这一项都大于更大的那个阈值了,肯定得是1,也就是block
- H k , n p = 0 H_{k,n}^p =0 Hk,np=0 if H k , n p < τ L o w H_{k,n}^p <\tau_{Low} Hk,np<τLow :这一项比更小的那个阈值都要小,得是0,也就是openning
- H k , n p = H k , n − 1 b H_{k,n}^p = H_{k,n-1}^b Hk,np=Hk,n−1b others :这一项不算大,也不算小,咋办?就维持前一时刻的状态吧,先观望一下。其中, H b H^b Hb 是二值化之后的极坐标直方图。
3、第三部分:限制机器人可选的前进方向
VFH算法中,机器人可选的前进方向是一圈360度都可能称为机器人的前进方向,看下图a。想一想这合适吗?我可不希望我的机器人一会向前,一会向后,一会向左,一会又向右,机器人的运动轨迹非常的不平滑。而且还有一个最大的问题,机器人很难进行高速的运动。想一想机器人的车轮正在飞速的旋转,机器人在欢快的向前奔跑,突然控制器发来命令,说,“嘿,老哥,你下一时刻的前进方向在你后面,跟现在的正相反”。机器人听了是什么感受,我正先前飞奔,你现在让我倒退,玩我呢?就算是电机再好,老这么搞,电机也是遭不住啊!
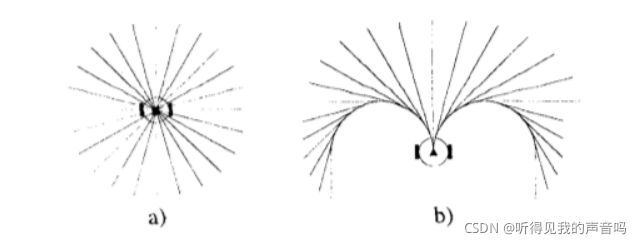
所以,VFH+算法对此作出了改进,限制了机器人可选的前进方向,看上图b,大大平滑了运动轨迹。骑过小电瓶车的小伙伴应该都有感受,车速越快,越是忌讳急转弯,太危险了,搞不赢就躺地上了啊。也就是说,车速越快,转弯半径越大,相应的曲率就越小;车速越慢,可以承受的转弯半径就越小,相应的曲率就越大。如此,机器人的可选择的前进方向就只有上图b中被两个(转弯)圆夹出来的部分。(姑且叫它转弯圆吧,这名字应该好理解吧。)
假如说机器人当前的速度是v ,对应的最小转弯半径是 R 。前面提过,障碍物的膨胀幅度是 r r + x r_{r+x} rr+x ,看下图
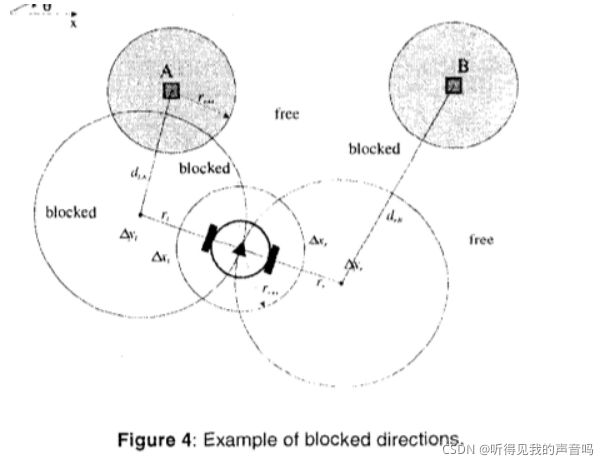
在机器人的前面存在两个障碍物A和B,这两个障碍物被膨胀之后分别为上图中两个阴影圆所示。机器人的左右侧两个转弯圆的半径为R,那么机器人会和障碍物碰撞的条件是什么呢?或者说满足什么条件的话,机器人很大概率上会撞上障碍物呢?上图中的障碍物A ,A 和左侧转弯圆的圆心的距离为 d C , A d_{C,A} dC,A 由于存在 d C , A < r r + x + R d_{C,A}
那么机器人是怎么实现避开A 的呢?下图中,b是第二部分二值化之后的极坐标直方图。由于障碍物A和机器人的左侧转弯圆有重合部分,再加上机器人可选择前进方向是两个转弯圆之间夹出来的部分,那么对于机器人来说,从A 障碍物开始逆时针旋转大半圈(一直转到右侧转弯圆为止)都不可以通过,都是block。这一来二值化的极坐标直方图就从b变成了c,这时候机器人该选择哪一个方向前进就一目了然了。

4、第四部分:方向选择
这一部分,对应VFH算法的第二部分——方向控制。只不过VFH是直接从第一步生成的极坐标直方图来生成方向,而VFH+是经过了第二部分和第三部分的处理之后才开始生成前进方向。
VFH +和VFH的方向产生一样,只不过,VFH在这一步——考虑目标方向、当前方向、前一时刻方向。什么意思呢?在VFH算法中,方向控制就是单纯的从极坐标直方图生成前进方向,没有考虑目标在哪里、当前的方向为何、前一时刻方向为何;而且由于工作空间的更新,方向控制生成的前进方向变化比较剧烈,这也是导致机器人频繁的原地摆头的原因。VFH+算法同时将目标方向、当前方向、前一时刻方向考虑进来。采用如下的代价函数来得到最佳的前进方向
g ( c ) = μ 1 ∗ Δ ( c , k t ) + μ 2 ∗ Δ ( c , θ n / α ) + μ 3 ∗ Δ ( c , k d , n − 1 ) g(c)=\mu_1*\Delta(c,k_t)+\mu_2*\Delta(c,\theta_n/\alpha)+\mu_3*\Delta(c,k_{d,n-1}) g(c)=μ1∗Δ(c,kt)+μ2∗Δ(c,θn/α)+μ3∗Δ(c,kd,n−1)
其中,第一项的 Δ \Delta Δ 是生成的前进方向和目标方向的差值,系数是 μ 1 \mu_1 μ1 ;第二项的 Δ \Delta Δ 是生成的前进方向和当前前进方向的差值,系数是 μ 2 \mu_2 μ2 ;第三项的 Δ \Delta Δ 是生成的前进方向和前一时刻前进方向的差值,系数是 μ 3 \mu_3 μ3 。通过配置三个系数的大小可以得到不同特性的VFH+算法。
如果是第一项的系数最大,那么无疑我们更加看中目标方向的作用,这时候得到目标导向的VFH+算法。相应的路径很可能不是那么光滑。此时最好满足关系 μ 1 > μ 2 + μ 3 \mu_1>\mu_2+\mu_3 μ1>μ2+μ3 。这是论文作者提出来的,我不是太理解,我的三个系数分别是2、2、1,感觉效果也挺好的。可能是我还没有发现一些东西吧。
如果第二项系数最大,那么说明我们更加看中路径的光滑程度。
如果觉得路径还是不够光滑,当然可以增大 μ 2 \mu_2 μ2 ,然而如果 μ 2 \mu_2 μ2 太大,比如 μ 1 \mu_1 μ1 是1, μ 2 \mu_2 μ2 是100,那说真的,还搞个什么劲啊,直接取消第一项算了。所以第二项的系数也不能大的离谱,这时候就可以加入第三项,来使得路径更加的光滑。
除此以外,还可以增加其他的项,比如我们还希望关注一下各个opening的宽度,这时候就可以考虑加入第四项将opening的宽度也纳入。