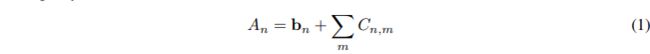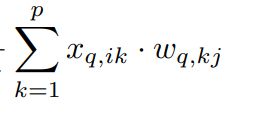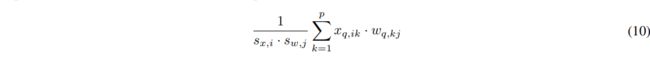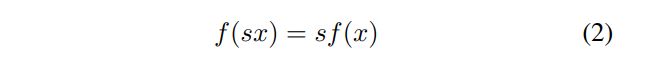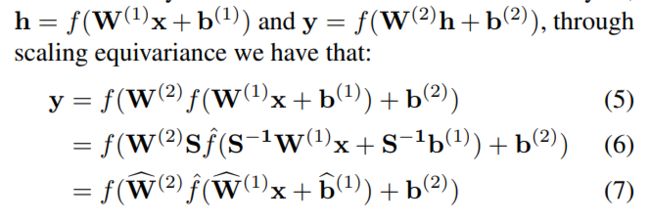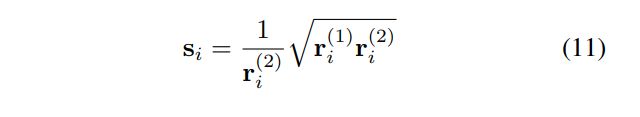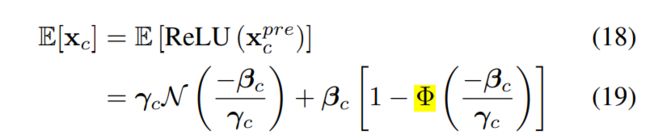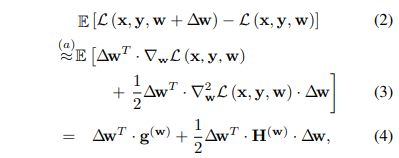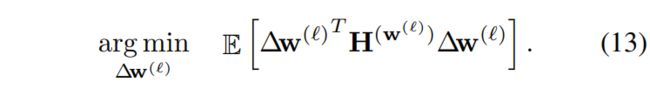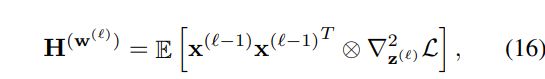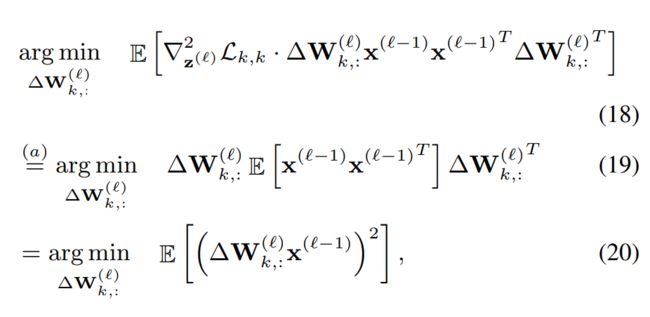模型量化（int8）系统知识导读

阿丘科技， 工业视觉的领导者，薪资 ok,  如 高级算法 30-60k ， 内推码： NTAHmCz

微信号 ：i_scream_andicecream 

内推的话，欢迎加好友

主要参考资料：

1、 TensorRT Developer Doc

2、 量化白皮书 高通 2021

3、 Data-Free Quantization Through Weight Equalization and Bias Correction 高通 2019

4、 Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation Nvidia 2020

5、github 量化doc合集

本文是深度学习模型量化的基础导引资料。主要阐述量化中概念、问题、解决方案。由于量化的内容研究比较少，很多论文都是研究型的文章（没有完成 从 0 到 1 工作的），所以本文只对比较完善的方法展开具体分析 。并对 TensorRT 中的量化代码实现，从 Nvidia 官网资料出发做第三方的解读。

量化的目的：是为了减少计算时间和计算能耗 。在一些场景下对能耗和时间的要求，要高于模型的指标，所以在这种情况下量化是一个必然的选择。

摘要

量化 : 量化一般是指将 F32 数据映射成 int8 的数据。泛指将F32映射为低 bit 的数值表示，如 int4、int8。量化的方法二值量化，线性量化、指数量化。

线性量化：对称量化（ Symmetric uniform quantization）和非对称量化（ 英文别名 Uniform affine quantization ）。其中对称量化计算量低于非对称量化。不常用的量化如 ：二次幂量化(Power-of-two quantizer)和二值量化。

量化粒度 ：量化粒度是指共享量化参数的大小，例如 每个 Tensor 共享一组量化参数，那么量化的粒度为 per-tensor。量化的粒度越小（最小精度是 per-col or per-row 下文解释原因），模型的精度越好，但计算成本越高。

网络结构往往会影响模型量化后的精度 ：conv-dw , BN floder ( 定义见下文) 会影响量化模型的精度。针对这个问题有两种解决方案：

1、权重量化采用 per-channel

2、Data free 论文中的算法流程

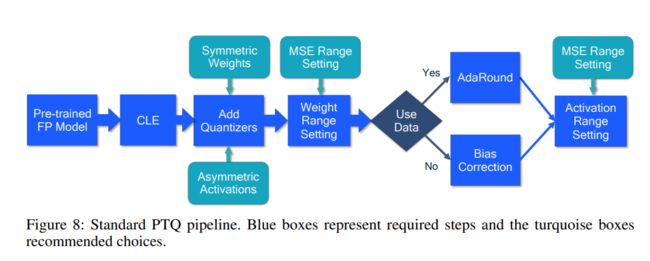
模型量化方法： 训练后量化(PTQ)和量化感知训练(QAT)。PTQ方法，是将已经训练好的模型进行量化，同时只需要很少的数据或者不需要数据，少部分需要手动调整的超参数以及不需要端到端训练。这使得PTQ成为一种工程实现简单并且不需要大量计算成本的量化方法。QAT，它依赖神经网络在训练过程中进行模拟量化。虽然QAT需要进行重新训练以及调整超参数，但是在低bit时却可以比PTQ获得更接近全精度的效果。

QAT 对于更低精度也是可以使用，如 int4 weight 量化，一般指标损失 2%~10%

精度提升方法 ： 部分量化，一些模型量化后精度损失往往是一些层导致的，这些层不进行量化，精度将大幅度提升； QAT 也是精度提升的有效方法；

硬件量化的过程

量化的目的是减少计算时间和能耗，但是这个计算实现是通过硬件实现的，所以量化要做的工作一定是和设备厂商有关的。目前市面上硬件支持的量化能找到的只有 int8，其余更低精度的量化都是在理论阶段。

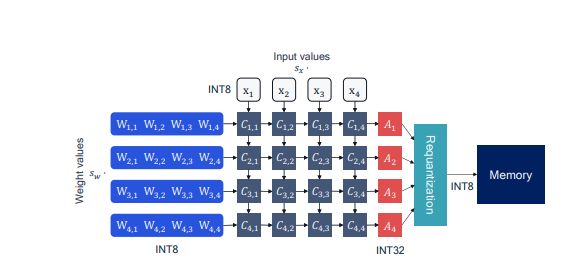
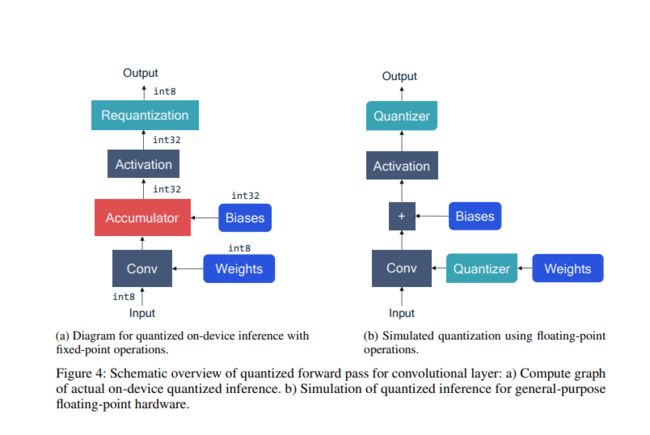
在 NPU 中，通常使用一个硬件实现 y = wx + b ，如下图所示

如下图所示（高通的硬件）， int8 的乘法，往往使用 int32 存储 bias 值（原因见下），相加后，将 int 32的值 再量化到 int8。

It is important to maintain a higher bit-width for the accumulators, typical 32-bits wide. Otherwise, we risk incurring loss due to overflow as more products are accumulated during the computation.

量化方法

量化的方案多种多样，这里重点介绍对称量化和非对称量化(这两个都是线性的)。

关键性总结：

1、 对称量化能够满足整个模型量化需求（nvidia 认为，TensorRT 全部使用对称量化）

2、 weight 量化中，非对称量化相比于对称量化代价较大（详情见文献4 3.3章节）

3、 激活函数的量化一般使用非对称量化，且量化成 uint8

Nvidia 中量化和反量化的概念

Quantize: convert a real number to a quantized integer representation (e.g. from fp32 to int8).

Dequantize: convert a number from quantized integer representation to a real number (e.g. from int32 to fp16).

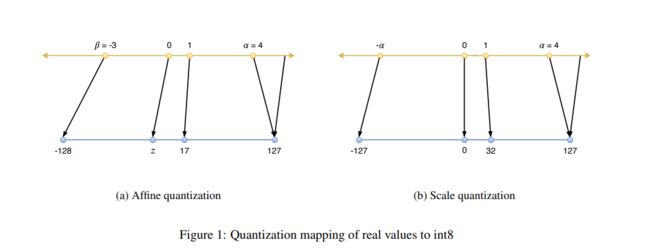
非对称量化

对称量化

Nvidia 通过实验给出 scale 量化 对于 int8 已经足够了

While both affine and scale quantization enable the use of integer arithmetic, affine quantization leads to more computationally expensive inference

Note that this extra computation is incurred only if affine quantization is used for the weight matrix. Thus, to maximize inference performance we recommend using scale quantization for weights. While affine quantization could be used for activations without a performance penalty, we show in later sections that scale quantization is sufficient for int8 quantization of all the networks we studied .

Power-of-two 量化

限制了 scale 缩放因子的值域，必须为 2 的指数。

二值量化

把权重量化为 2 值

量化参数的计算（Calibration）

要点解析：

1、Weight 量化不需要数据就可以完成，

2、ReLU 的量化需要收集数据

3、没有依据证明哪种方法要好

上文对称量化和非对称量化中，需要通过选取 float32 值域的最大值 α 和最小值 β ，然后才能计算出 scale，Nvidia 隐式量化中称此过程为 calibration。

Nvidia calibration:

In post-training quantization, TensorRT computes a scale value for each tensor in the network. This process, called calibration, requires you to supply representative input data on which TensorRT runs the network to collect statistics for each activation tensor.

补充： Nvidia 默认使用 KL 散度（相对熵）

量化粒度

关键性总结：

1、 量化的量化粒度越小， 模型的精度损失越小，但是计算量越大。

2 、激活层的量化使用 per-tensor 就已经足够 。

3、 卷积或者反卷积使用 per-tensor 或 per-channel

4、 量化最小粒度为 per-col 或者 per-row, 实际使用中只有 per-tensor, per-channel

Nvidia 量化粒度的介绍

There are several choices for sharing quantization parameters among tensor elements. We refer to this choice as quantization granularity. At the coarsest, per-tensor granularity, the same quantization parameters are shared by all elements in the tensor. The finest granularity would have individual quantization parameters per element. Intermediate granularities reuse parameters over various dimensions of the tensor - per row or per column for 2D matrices, per channel for 3D (image-like) tensors, etc

矩阵乘法中的 w*x 反量化表示：

由于实际的量化计算中， w 和 x 都被量化了然后进行计算（使用上面的硬件）, 只能得到量化后的 yij 如下式 ，如果由下式可以得到公式 9 必然存在下述关系。

如果能够使用整数矩阵乘法（即通过上式得到 公式 9），那么公式 9 必须等于 公式 10，即 w*x ，w 每一行共享一组量化参数 , x 每一列共享一组量化参数

量化的粒度就是共享量化参数的范围，根据上述所知 最小的量化粒为 per-row 或者 per-cow

影响模型指标的因素和方案

关键性总结：

1、weight 量化粒度为 per-tensor , BN Floder 和 conv-dw 在一起使用会使模型量化后的指标严重下降

2、 两种解决方案：

a、权重量化粒度选用 per-channel

b、Data-free 的算法流程

其中 b 方案 应用场景，在设备只支持 per-tensor 量化

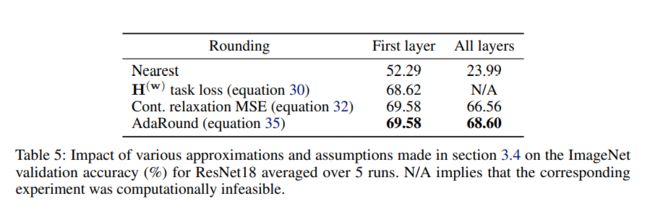
3、AdaRound 目的是为了减少量化误差（per-tensor per-channel 都可以用）

BN Floder

BN 在推理中 ，可以被当收到上一层的权重和偏置中，如下面公式 14

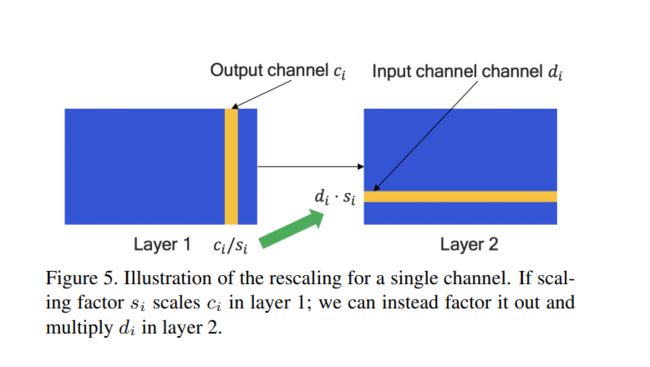
BN 折叠进卷积后，上一层 weight 相当于发生了线性变化，使 weight 的 channel 维度上差异更大。

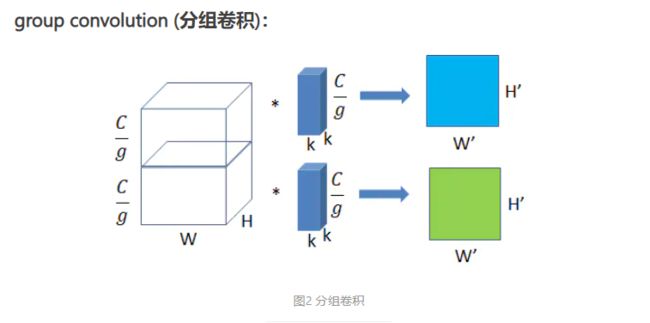
Con-dw

上图为分组卷积， 如果组和上层的通道数相同，那么为 conv-dw。每个通道的权重的分布是不同的，如果权重使用 per-tensor 进行量化，必然会造成会造成模型指标的下降。如果将量化粒度采用 per-channel ，即可以解决这个问题。

Nagel et al. (2019) showed that this is especially prevalent in depth-wise separable layers since only a few weights are responsible for each output feature and this might result in higher variability of the weights.

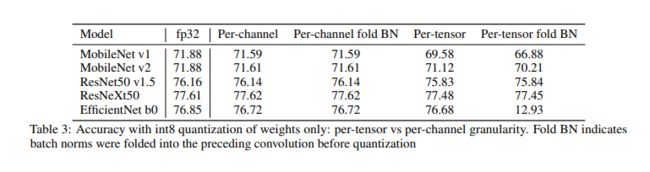
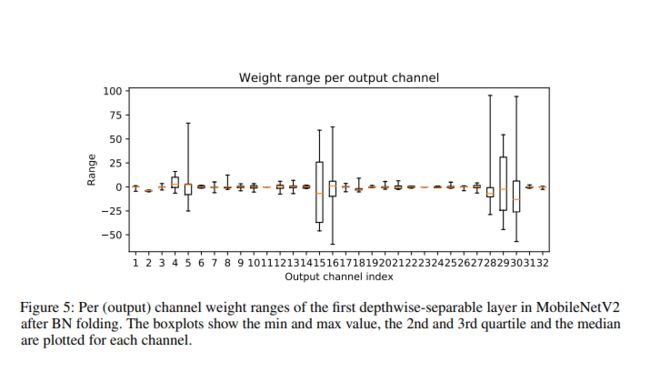
当 BN floder + per-tensor + con-dw 的组合出现时（下图出自文档3，实验框架： pytorch + TensorRT）：

Con-dw 特性 :

BN floder 会加剧 conv-dw weight 差异， 上图展示了 MobileNetV2 depthwise 的中 channel 的数据分布。此图可以知道 BN floder 后 con-dw weight channel 的数据分布差异巨大。此时用相同的量化参数去进行量化，必然导致一些量化的结果严重失真。

Data-Free 算法

有些设备不支持 Per-channel 量化 ，就可以使用 Data-free quantization 论文中的工作。

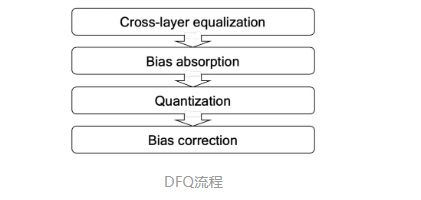
Data free 算法的流程：

Cross-layer equalization

Relu 等线性函数存在以下性质( s>0) ：

神经网络中存在两个相邻的层，存在下面这样的性质：

那么问题建模成： 寻找 S 矩阵 ，使输出 channel 的值更加均衡(卷积可以用乘法表示 不同 channel )

将每层的精度（每个 channel 越均衡精度越高），建模成 pi 公式如下：

可以理解以成，将本层不均衡 ，一部分代价转移到相邻层，让相邻层一起承担，所以要将这种代价变的最小，所以目标函数如下所示。

在对称量化, 根据上述目标函数 ，求解结果：

Bias absorption

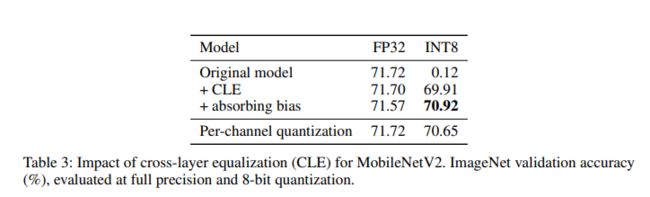
上述 Cross-layer equalization 中的目标函数，没有对 bias 的限制, bias absorption 就是对 bias 做修正，即在激活函数后直接减去这个偏移。

当 si <1 时，相当于本层的输出更加均衡，使上一层变得更加不均衡, 会使 bias 变大。会使 active 量化的范围变大（wx + b）, 为了解决这个问题 ，直接减去 c

效果如下：

量化误差

量化会造成一种激活的偏差，会使整个数值的分布发生偏移。

四舍五入是这种量化误差的主要原因（int8、int 4)。

这种偏移在 con-dw 更容易发生

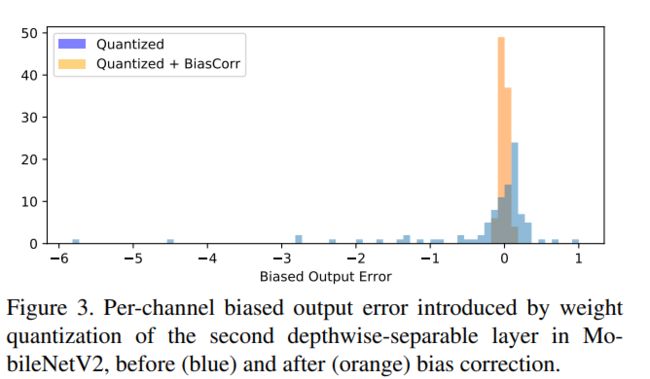
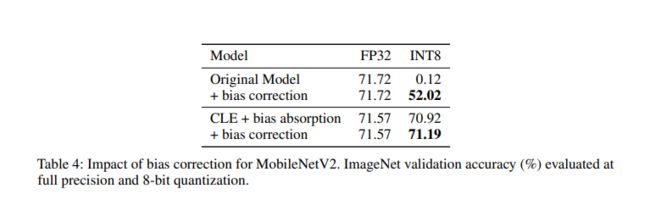
Bias correction

如何去抵消误差（直接减去）：

模型量化的偏移（这个公式是）

其中， w~ 是量化后再反量化的 weight (即带了量化误差)， w 是原先的 weight， x 是输入，对应的 y~  是量化后的输出， y 是原输出。

那么无偏估计如上公式1所示，根据数据估计出每层的偏移误差（将偏移拉回就可以），将偏移误差抵消加入。

如果可以得到数据，可以直接

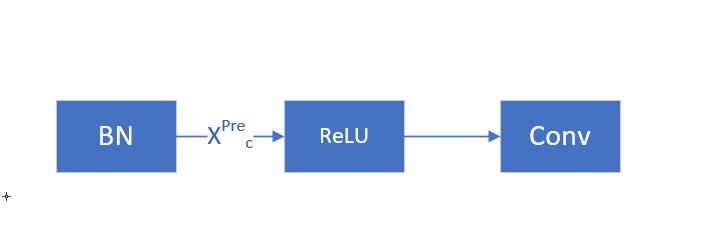
可以利用 BN 的性质，BN 本质上就是正太化，γ 就是 XPrec 的均值， 经过 ReLU 后的均值如下公式所示，通过 E[y] , 可以估算出 ε 的大小。

效果如下图：

AdaRound

四舍五入会导致量化误差 （或者说四舍五入不是最优的），那是否能找到一种方案替代四舍五入。

量化误差用（如下公式） ，泰勒展开公式展开

模型收敛时，g(w) 近似为 0， 所以目标函数：

求解公式 13 求解遇到的困难

为了规避求解困难的问题，将目标函数：

Hassion 求解困难，原因是需要上一层的 二阶矩

假设，上一层的二阶矩是对角意义（简化了问题 物理意义上下层的 weight 不存在关系 ）

那么目标函数就变得简单起来

为了解决 NP 问题，对上式条件进行放缩，将 0-1 问题，转化为连续问题 h(V) 的值域为 0 ~1， Vi,j 的取值范围是连续的变量，为了使 h 函数收敛到 0 或者 1，增加正则项 公式34， 将激活函数加入目标函数 35， 可以通过类似训练网络的的方法进行求解。

展示：

量化感知训练（Quantization-Aware-Training）

关键性总结：

1、QAT 往往用于更低精度的量化（例如 Int4）,或者可以当作提升模型精度的手段

2、量化感知训练的网络结果与普通 F32 模型训练相比，只是插入了 Fake 量化节点。

QAT int 量化的效果展示：

weight int4 量化效果图：

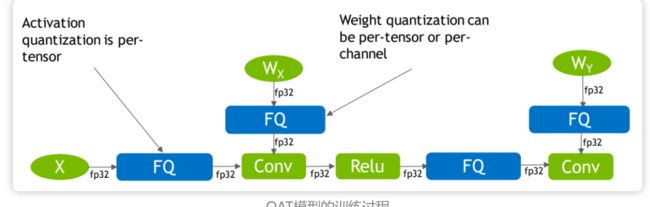
模拟量化

模拟量化，就是在模拟量化的过程， 在真实量化的地方插入 fake 量化节点，然后训练模型。

Fake quantizer 就是先进行量化 ，然后进行反量化，如下公式所示。

下图为 google（Tensorflow）论文中的模拟量化示意图，不同的硬件处理方式不同。

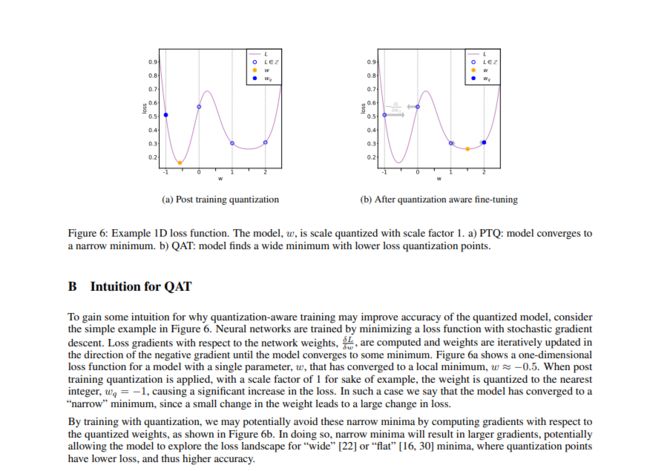
QAT 提升模型准确率的依据

QAT 注意事项

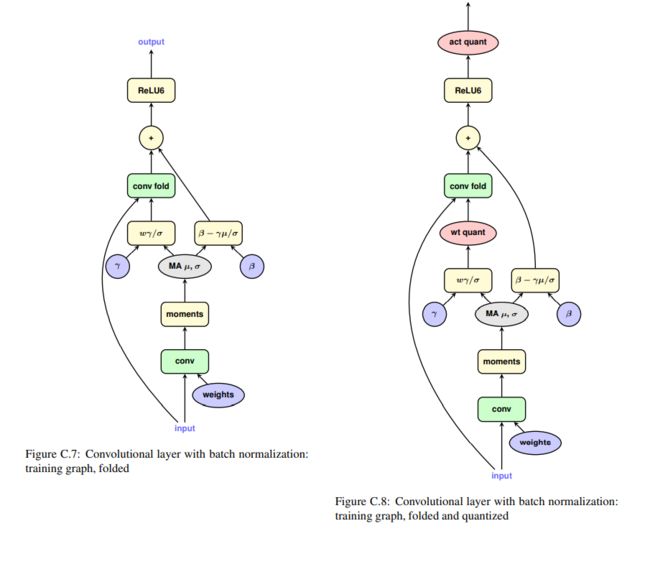
插入Fake 节点

先验信息： QAT 是为了提高模型的准确率，进行再训练，最后还是使用推理框架执行（TensorRT ）

如： 推理中会将 Batch Normal 融合到相邻的 conv 中。

所以在模拟量化时

Straight-through estimator

Fake 节点中，使用 clip 函数，clip 梯度为处处为 0 或者未定义，解决这个问题的一种方法是使用直通估计器（straight-through estimator STE，Bengio et al. 2013）来近似梯度，它将舍入算子的梯度近似为 1。

利用这个近似值，现在我们可以从方程（7）中计算出量化操作的梯度。为了清楚起见，我们默认使用对称量化，即 z = 0，但同样的结果适用于非对称量化，因为零点是一个常数。我们使用 n 和 p 来定义整数量化范围，如 n = qmin/s ， p = qmax/s。梯度与它的输入xi被如下定义：

这样在反向梯度传播时，可以直接跳过 fake 量化节点。

STE 在低精度（2bit）量化感知训练中存在问题, 导致模型很难收敛，或者收敛慢

解决方案论文： https://arxiv.org/abs/1908.0503

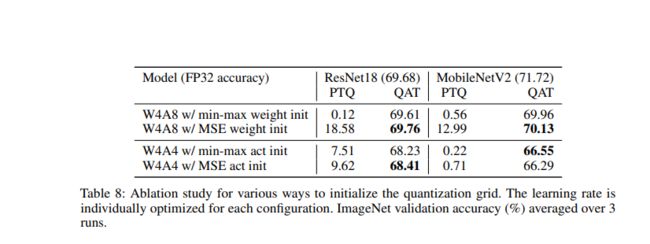
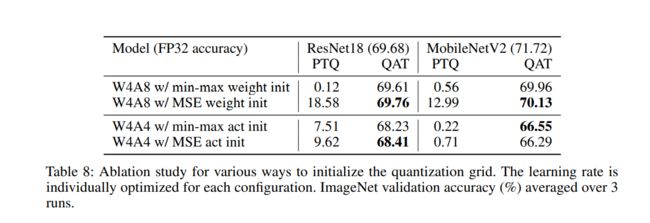
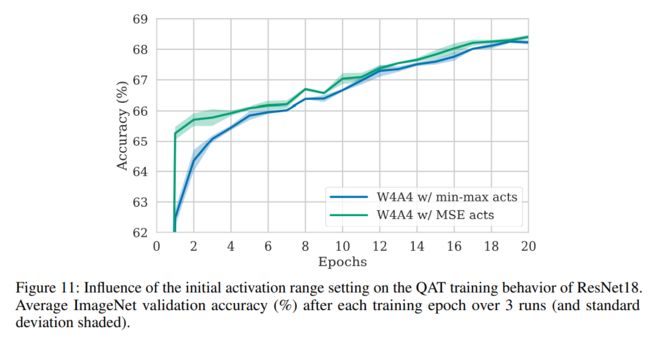
QAT 的初始化

不同的初始化方式，还是会影响收敛效果

Nvidia 的建议：

QAT 的初始化和超参数的选择也是要注意的。

二值网络

二值网络，就是通过二值量化 和 STE使用量化训练的流程。

Yoshua Bengio作为BNN（2016）的开山祖师，不仅给众多人指明了山的方向。

二值网络综述

关键性总结：

1、第一层和最后一层采用全精度（具体原因看论文综述）

2、下采样全精度（下采样如果使用二值 会导致丢失了巨大的信息量，以至于整个网络就无法使用）

3、加入shortcut 和 concat 会大大提升性能。

2、3  可以理解为一些网络结构对量化友好，一些结构是不友好的。

1、BNN 梯度问题

使用了STE之后，实值的weights就可以使用如SGD和Adam这样常见的优化器来进行更新了，同时考虑到这个实值weights是没有设置边界的，这样它就有可能会一直累加到特别大的值，从而与二值化的weights之间的量化误差越来越大，积重难返，所以作者对实值的weights还单独加了一个截断函数clip(x,-1,1)，将其限制在-1和+1之间，这样使得实值weights和二值化weights的距离更近。

对于activations的二值化和weights是相似的，并且在实验中作者发现，当sign函数的输入的绝对值大于1的时候，将梯度置0可以得到更好的实验结果。

简单总结一下，我们可以看到作者在训练过程中对weights和activations做了不同的设置，两个在梯度更新上都是遵照STE的原则，直接将sign函数跳过，而实值weights在更新之后会裁剪到[-1,1]之间，从而减小实值weights和二值化weights之间的距离，而activations的梯度在更新的时候，当实值activations的绝对值大于1时会将梯度置0，避免特别大的梯度向下传递使得训练时候出现震荡

2、XNOR-Net 论文中两个模型，BWN 和 XNOR-Net

BWN 中weight 二值化，active 全精度 ，对分类任务中的模型指标无伤（这些模型都不含 con-dw）

XNOR-Net 研究量化误差，恢复量化误差，论文中效果特别好，但是综述上说 结果无法复现，但是阐明了研究方向

XNOR-Net 并且提出了对实值weights每个输出通道方向上提取出一个scaling factor，用于恢复二值化weights的信息，同时对activation在HW方向上每个pixel上提取一个scaling factor，用于恢复二值化activations的信息，这两种scaling factor都无需学习，直接计算相应的L-1范数就能得到，且不影响二值化高效的卷积计算过程。

3、 IR-NET

这篇论文主要针对的是二值化在前向计算和反向梯度传播中带来的信息损失问题，作者分别提出了两个技术，一个是 Libra-PB(Libra Parameter Binarization)，用于在前向计算中同时最小化weights的量化损失和信息熵损失，另一个是EDE(Error Decay Estimator)，通过渐进近似sign函数来最小化反向传播过程中梯度的信息损失。 Libra-PB简单来说就是在weights被二值化之前，先对它做归一化处理，即减均值除方差，这样的话在二值化之前，就大概有一半的weights是大于0，一半的weights小于0，从而使得二值化之后的weights信息熵损失最小。

而EDE则是利用k×tanh(t×x)在不同训练阶段渐进近似sign函数，并用其梯度来代替sign函数的梯度进行反向传播，从而使得整个训练过程可以更加的平滑，从而减少信息损失。

总结：

1. 1. Gain term 增益项

这个主要指的是一些为了减少数据二值化损失而增加的一些额外的项，如XNOR-Net首次提出的在weights二值化之前计算一个channel-wise的scaling factors(一般是每个通道权重的均值)用于恢复量化损失，这个思想被沿用至今简单有效。 还有各种在activations上增加的可学习的参数，如ReActNet提到的RSign和RPReLU，这些增益项虽然增加一点点的计算，但对模型精度却有大幅度的提升。另外要说明的XNOR-Net里面对activations在HW方向上每个pixel计算一个scale，这个虽然可以减少二值化的信息损失，但是在前向过程中对推理速度的影响很严重，所以暂不列入其中，这也说明了一点，weights上的增益项无论是可学习的还是在线计算的都不会对推理速度有较大影响，因为训练结束之后可以得到固定的系数。而activations的增益项最好是用可学习的，因为在前向推理过程中，每次输入数据不同，在线计算的增益项都需要重新计算，这个对推理速度影响很大。

b. 多个二值化base

这个特指ABC-Net的做法，用多个二值化的base线性加权近似全精度的weights和activations，性能不错，典型的以时间和空间换取精度的做法。

c. 二值友好的结构设计

Bi-Real Net，BinaryDenseNet和MeliusNet三篇论文验证了在BNNs网络结构中加入shortcut和concat操作能够大大增强模型的Quality和Capacity，从而大大提升性能。

d. 关键层的设计

神经网络中关键层一般指的第一层，下采样层和最后一层，这些层相对于其他普通层对模型性能影响更大，所以需要额外注意。

第一层的输入是原始数据，且卷积核的参数量较少，如果第一层出现了巨大的信息损失，那么后面层基本上也学不到啥了，原始BNN论文没有对输入直接二值化，因为输入的图像数据是UINT8类型，范围[0,255]，二值化基本都是1了，信息损失殆尽，所以作者直接输入原始的数据与二值weights进行卷积计算。为了提升计算效率，作者将输入按比特位切片出来，用移位和XNOR代替乘法，如下图所示。

但这个做法不太妥当的是，输入数据虽然没有丢失信息，但是没有做数据的归一化。在主流的模型训练中我们可以知道，数据的normalize对结果影响还蛮大的，所以目前主流的BNNs基本上第一层都是使用全精度的卷积层，输入数据正常归一化处理后输入网络，因为通常认为这块计算量不大。但是MeliusNet在实验中发现目前很多BNNs计算中，浮点计算占了60%以上，第一层很多人使用的7×7的卷积核，计算量还是蛮大的，所以MeliusNet用三个3×3的卷积进行了代替，节省了一半的计算。

下采样层的特点是图像分辨率会直接减少一半，这个过程是一个不可逆的信息损失的过程。早期的BNNs都倾向于使用MaxPooling来进行下采样操作，但是存在一个问题是，如果在每一层activations二值化之后进行MaxPooling，会导致梯度反传到这块的时候将梯度均匀的分给多个+1或者多个-1，然而实际上只有real-value最大的那个值真正起了作用，这样的分配是不公平的，所以比较好的做法是遇到MaxPooling操作的时候，将activations的二值化延后，对实值的weights进行下采样，这样可以得到更好的效果。但目前的网络设计人员通常认为MaxPooling是不可学习的算子，倾向于使用stride=2的卷积层来进行下采样，这样可以保留更多的信息，所以在目前的BNNs当中，这块通常也是使用全精度的卷积来计算，避免造成较大精度损失，同时可以利用组卷积+channel shuffle的方式来进一步降低浮点的计算量。

这一层在分类任务中通常是全连接的结构，输出最后的预测结果，为了避免二值化的影响，通常也是采取全精度的计算，本来想提一下很多人对FC做的random pruning能降低计算，但又仔细想了想，这中任意剪枝方式在硬件上实现尤为麻烦，估计很难加速。

恢复量化的指标方法

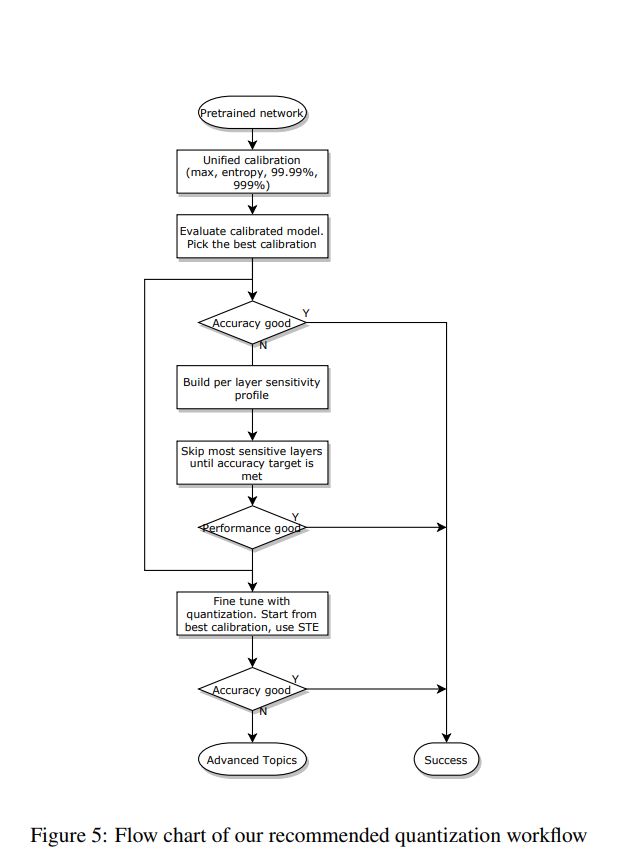
方案：

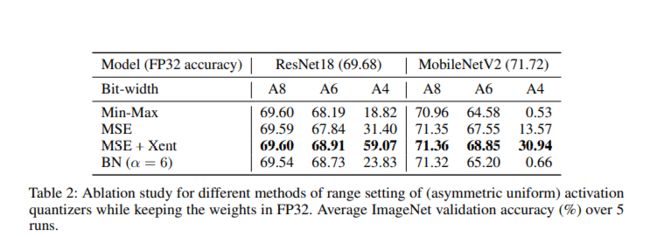
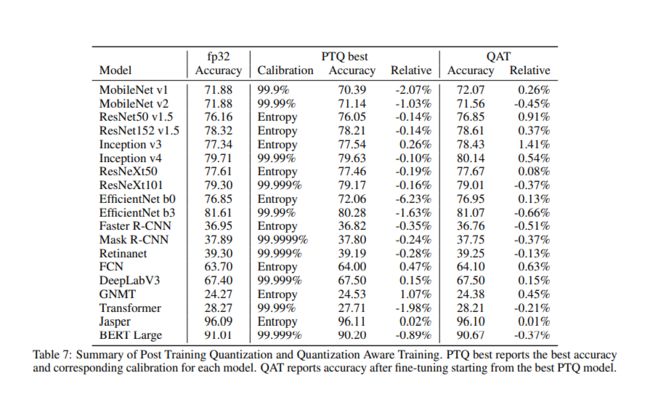
1、 选择最优的 calibration 算法

2、 部分量化

3、 QAT

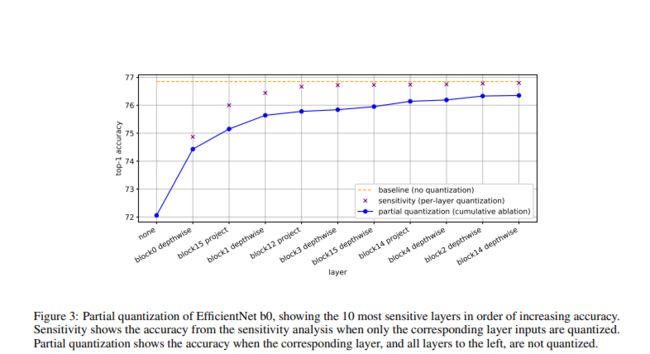
部分量化

在模型量化中往往只有几层网络的量化影响模型的指标，可以做单层量化对模型指标的敏感度分析，即分别量化网络的单层，统计指标下降，指标下降多的层不量化。

部分量化的效果：

Nvidia 的建议: