傅里叶级数与傅里叶变换_Part5_傅里叶级数推导傅里叶变换
傅里叶级数与傅里叶变换_Part5_傅里叶级数推导傅里叶变换
0、复习Part4的内容
对于周期为 T T T,即 f ( t ) = f ( t + T ) f\left( t \right) = f\left( {t + T} \right) f(t)=f(t+T)的函数,它的傅里叶级数的复数展开形式如下:
f ( t ) = ∑ n = − ∞ ∞ c n e i n ω t f\left( t \right) = \sum\limits_{n = - \infty }^\infty {{c_n}{e^{in\omega t}}} f(t)=n=−∞∑∞cneinωt, 其中, c n = 1 T ∫ 0 T f ( t ) e − i n ω t d t {c_n} = \frac{1}{T}\int_0^T {f\left( t \right){e^{ - in\omega t}}dt} cn=T1∫0Tf(t)e−inωtdt
重写一下
f T ( t ) = ∑ n = − ∞ ∞ c n e i n ω 0 t ( 1 ) {f_T}\left( t \right) = \sum\limits_{n = - \infty }^\infty {{c_n}{e^{in{\omega _0}t}}} {\rm{(1)}} fT(t)=n=−∞∑∞cneinω0t(1), ω 0 = 2 π T {\omega _0} = \frac{{2\pi }}{T} ω0=T2π为角频率。
c n = 1 T ∫ 0 T f T ( t ) e − i n ω 0 t d t = 1 T ∫ − T 2 T 2 f T ( t ) e − i n ω 0 t d t ( 2 ) {c_n} = \frac{1}{T}\int_0^T {{f_T}\left( t \right){e^{ - in{\omega _0}t}}dt} = \frac{1}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {{f_T}\left( t \right){e^{ - in{\omega _0}t}}dt} {\rm{(2)}} cn=T1∫0TfT(t)e−inω0tdt=T1∫−2T2TfT(t)e−inω0tdt(2)
在上式中, ∑ n = − ∞ ∞ e i n ω 0 t \sum\limits_{n = - \infty }^\infty {{e^{in{\omega _0}t}}} n=−∞∑∞einω0t可以理解一种规则,而 c n c_n cn呢,我们可以理解为它定义了函数, c n = a + b i {c_n} = a + bi cn=a+bi是一个复数。
用图像的表达形式如下
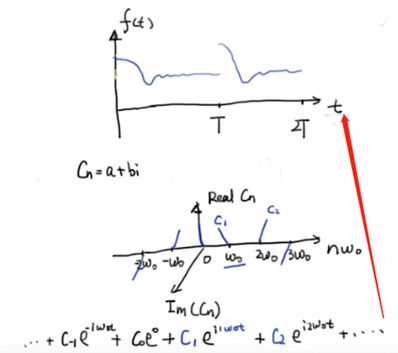
我们称上面的图为时域表达,下面的图为频域表达。 工程上一般会取 ∣ c n ∣ \left| {{c_n}} \right| ∣cn∣专门来看幅值。
1、由傅里叶级数推导傅里叶变换
对于一个非周期函数,也就说它不重复, T → ∞ T \to \infty T→∞。
lim T → ∞ f T ( t ) = f ( t ) \mathop {\lim }\limits_{T \to \infty } {f_T}\left( t \right) = f\left( t \right) T→∞limfT(t)=f(t)
我们定义,两个频率之间的距离 Δ ω ≜ ( n + 1 ) ω 0 − n ω 0 = ω 0 = 2 π T \Delta \omega \triangleq \left( {n + 1} \right){\omega _0} - n{\omega _0} = {\omega _0} = \frac{{2\pi }}{T} Δω≜(n+1)ω0−nω0=ω0=T2π。
当 T ↑ , Δ ω ↓ T \uparrow ,\Delta \omega \downarrow T↑,Δω↓, T → ∞ , Δ ω = 0 T \to \infty ,\Delta \omega = 0 T→∞,Δω=0。
离散的形式→连续的形式,Cn那个图就变成了三维空间的一条连续的曲线啦。 我们横轴的 n ω 0 n{\omega _0} nω0,也可以变成 ω \omega ω 啦。
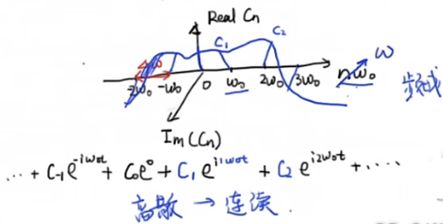
我们现在把最开始的(2)式带入到(1)式当中,可以得到
f T ( t ) = ∑ n = − ∞ ∞ 1 T ∫ − T 2 T 2 f T ( t ) e − i n ω 0 t d t e i n ω 0 t {f_T}\left( t \right) = \sum\limits_{n = - \infty }^\infty {\frac{1}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {{f_T}\left( t \right){e^{ - in{\omega _0}t}}dt} {\rm{ }}{e^{in{\omega _0}t}}} fT(t)=n=−∞∑∞T1∫−2T2TfT(t)e−inω0tdteinω0t
根据 Δ ω \Delta \omega Δω的定义, Δ ω ≜ 2 π T ⇒ 1 T = 2 π Δ ω \Delta \omega \triangleq \frac{{2\pi }}{T} \Rightarrow \frac{1}{T} = \frac{{2\pi }}{{\Delta \omega }} Δω≜T2π⇒T1=Δω2π。因此上式可进一步表达为:
f T ( t ) = ∑ n = − ∞ ∞ Δ ω 2 π ∫ − T 2 T 2 f T ( t ) e − i n ω 0 t d t e i n ω 0 t {f_T}\left( t \right) = \sum\limits_{n = - \infty }^\infty {\frac{{\Delta \omega }}{{2\pi }}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {{f_T}\left( t \right){e^{ - in{\omega _0}t}}dt} {e^{in{\omega _0}t}}} fT(t)=n=−∞∑∞2πΔω∫−2T2TfT(t)e−inω0tdteinω0t
此时,我令 T → ∞ T \to \infty T→∞
f T ( t ) → f ( t ) {f_T}\left( t \right) \to f\left( t \right) fT(t)→f(t)
∫ − T 2 T 2 d t → ∫ − ∞ ∞ d t \int_{ - \frac{T}{2}}^{\frac{T}{2}} {dt} \to \int_{ - \infty }^\infty {dt} ∫−2T2Tdt→∫−∞∞dt
n ω 0 → ω n{\omega _0} \to \omega nω0→ω
∑ n = − ∞ ∞ Δ ω → ∫ − ∞ ∞ d ω \sum\limits_{n = - \infty }^\infty {\Delta \omega } \to \int_{ - \infty }^\infty {d\omega } n=−∞∑∞Δω→∫−∞∞dω
因此,上式可进一步化为:
f ( t ) = 1 2 π ∫ − ∞ ∞ ∫ − ∞ ∞ f ( t ) e − i ω t d t e i ω t d ω f\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {f\left( t \right){e^{ - i\omega t}}dt} {e^{i\omega t}}d\omega } f(t)=2π1∫−∞∞∫−∞∞f(t)e−iωtdteiωtdω
定义
F ( ω ) ≜ ∫ − ∞ ∞ f ( t ) e − i ω t d t F\left( \omega \right) \triangleq \int_{ - \infty }^\infty {f\left( t \right){e^{ - i\omega t}}dt} F(ω)≜∫−∞∞f(t)e−iωtdt , 这就是傅里叶变换。
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω f\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {F\left( \omega \right){e^{i\omega t}}d\omega } f(t)=2π1∫−∞∞F(ω)eiωtdω, 这就是傅里叶逆变换。
扩展:我们令 s = i ω s = i\omega s=iω, F ( s ) = ∫ − ∞ ∞ f ( t ) e − s t d t F\left( s \right) = \int_{ - \infty }^\infty {f\left( t \right){e^{ - st}}dt} F(s)=∫−∞∞f(t)e−stdt,这就是Laplace变换啦
系列学习链接:欢迎大家点赞、收藏、留言讨论。
傅里叶级数与傅里叶变换_Part0_欧拉公式证明+三角函数和差公式证明
傅里叶级数与傅里叶变换_Part1_三角函数系的正交性
傅里叶级数与傅里叶变换_Part2_周期为2Π的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part4_傅里叶级数的复数形式
傅里叶级数与傅里叶变换_Part5_傅里叶级数推导傅里叶变换
傅里叶级数与傅里叶变换_Part6_离散傅里叶变换推导
傅里叶级数与傅里叶变换_Part7_离散傅里叶变换的性质