机器学习(周志华)第一章至第三章笔记
关于周志华老师的《机器学习》这本书的学习笔记
记录学习过程
本博客记录Chapter1 to Chapter3
文章目录
-
-
- 1 绪论
-
- 1.1 引言
- 1.2 基本术语
- 1.3 假设空间
- 1.4 归纳偏好
- 1.5 发展历程
- 2 模型估计与选择
-
- 2.1 经验误差与过拟合
- 2.2 评估方法
- 2.3 性能度量
- 2.4 比较检验
- 2.5 偏差和方差
- 3 线性模型
-
- 3.1 基本形式
- 3.2 线性回归
- 3.3 对数几率回归
- 3.4 线性判别分析(LDA)
- 3.5 多分类学习
- 3.6 类别不平衡问题
-
1 绪论
1.1 引言
机器学习是关于“学习算法”的学问。
1.2 基本术语
-
特征向量(feature vector): x i = { x i 1 , x i 2 , … , x i d } x_i = \{x_{i1},x_{i2},…,x_{id}\} xi={xi1,xi2,…,xid}
-
维数(dimensionality):属性总数 d d d
-
预测:预测值离散—分类;预测值连续—回归;还有聚类
-
根据训练数据是否有标记信息:监督学习(supervised learning)和无监督学习(unsupervised learning)。分类和回归是前者;聚类是后者。
-
训练模型适用于新样本的能力称为“泛化”。
1.3 假设空间
归纳学习:induction,从特殊到一般的泛化过程。
学习过程是在所有假设(hypothesis)组成的空间中搜索的过程,搜索目标是找到与训练集匹配的假设。
1.4 归纳偏好
机器学习算法在学习过程中对某种类型假设的偏好,称为归纳偏好(inductive bias)
-
奥卡姆剃刀(Occam’s razor):若有多个假设与观察一致,则选择最简单的那个。例如认为“更平滑”意味着“更简单”。
假设样本空间 χ \chi χ和假设空间 H H H都是离散的。
令 P ( h ∣ x , ζ a ) P(h|x,\zeta_a) P(h∣x,ζa)是代表算法 ζ a \zeta_a ζa在训练数据 X X X产生假设 h h h的概率。令 f f f代表真是目标函数。训练集外误差:
E o t e ( ζ a ∣ X , f ) = ∑ h ∑ x ∈ χ − X P ( x ) Ⅱ ( h ( x ) ≠ f ( x ) ) P ( h ∣ X , ζ a ) E_{ote}(\zeta_a|X,f)=\displaystyle\sum_h \sum_{x \in \chi-X}P(x)Ⅱ(h(x)\neq f(x))P(h|X,\zeta_a) Eote(ζa∣X,f)=h∑x∈χ−X∑P(x)Ⅱ(h(x)=f(x))P(h∣X,ζa)
其中, Ⅱ Ⅱ Ⅱ表示指示函数,为真取1为假取0。
- NFL定理(没有免费午餐):当所有问题出现的机会相同,即所有问题同等重要的情况下,所有学习算法的期望性能相同。( E o t e E_{ote} Eote相同)。其重要意义在于让我们认识到脱离具体问题,空谈算法好坏毫无意义。
1.5 发展历程
推理—>知识—>学习
归纳逻辑程序设计(Inductive Logic Program,ILP):决策树,不适用于问题规模极大的情况
基于神经网络的连接主义:BP神经网络,黑箱模型,调参困难
统计学习(statistical learning):支持向量机,核方法。
深度学习:连接主义,多层神经网络。拥有大量参数,样本数据少容易过拟合。
2 模型估计与选择
2.1 经验误差与过拟合
-
经验误差: m m m个样本中 a a a个分类错误,则错误率 E = a m E=\displaystyle\frac{a}{m} E=ma。精度为 1 − E 1-E 1−E。学习器在训练集上的误差称为经验误差或训练误差。在新样本上的误差称为泛化误差。我们希望得到泛化误差小的学习器。
-
过拟合:学习器把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,导致泛化能力下降。
2.2 评估方法
-
用测试误差作为泛化误差的近似。
-
划分测试集和训练集的方法:
-
留出法:直接将数据集划分为两个互斥的集合。 D = S ∪ T , S ∩ T = ∅ D=S\cup T, S\cap T=\varnothing D=S∪T,S∩T=∅
- 结果:多次随机划分结果的平均值
- 一般将 2 / 3 , 4 / 5 2/3,4/5 2/3,4/5的数据用于训练集,剩余数据作为测试集
-
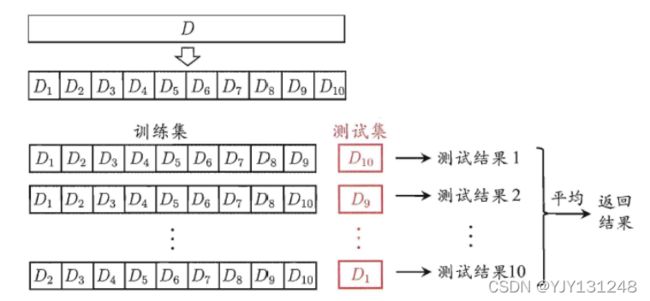
交叉验证法:将数据集划分为 k k k个大小相似的互斥子集。
- k = 10 k=10 k=10:十折交叉验证
- k = m ( 样 本 数 ) k=m(样本数) k=m(样本数):留一法,结果可靠但是运算复杂,计算开销大
-
自助法(bootstrapping):以自助采样法(bootstrap sampling)为基础,给定包含 m m m个样本的数据集 D D D,对他采样产生数据集 D ′ D' D′:每次随机从 D D D中挑选一个样本加入到 D ′ D' D′并放回,重复该过程 m m m次。
- 简单估计,样本在 m m m次采样中均不被采样的概率 p = ( 1 − 1 m ) m ≈ e − 1 ≈ 0.368 p=(1-\displaystyle\frac{1}{m})^m \approx e^{-1} \approx 0.368 p=(1−m1)m≈e−1≈0.368
- 适用于数据集较小、难以有效划分训练集和测试集的情况。
-
-
调参和最终模型:
- 参数分为算法的参数(超参数,数量一般在10以内)和模型的参数(很多)
2.3 性能度量
-
回归:均方误差(mean squard error)
M S E = E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 MSE = E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^2 MSE=E(f;D)=m1i=1∑m(f(xi)−yi)2 -
分类任务:
-
精度: a c c ( f ; D ) = 1 m ∑ i = 1 m Ⅱ ( f ( x i ) ≠ y i ) acc(f;D)=\frac{1}{m}\sum_{i=1}^{m}Ⅱ(f(x_i)\neq y_i) acc(f;D)=m1∑i=1mⅡ(f(xi)=yi)
-
错误率: E ( f ; D ) = 1 − a c c ( f ; D ) E(f;D)=1-acc(f;D) E(f;D)=1−acc(f;D)
-
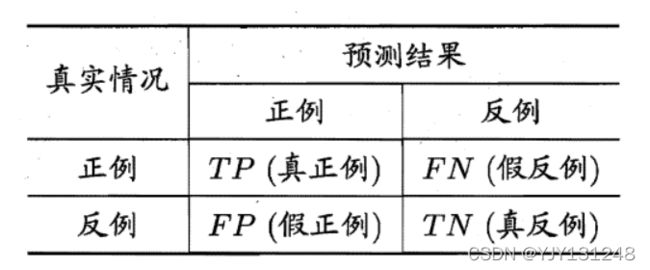
混淆矩阵
-
查准率: p r e c i s i o n = T P T P + F P precision = \displaystyle\frac{TP}{TP+FP} precision=TP+FPTP
-
查全率: r e c a l l = T P T P + F N recall=\displaystyle\frac{TP}{TP+FN} recall=TP+FNTP
- 查全率和查准率是一堆矛盾的较量
-
B E P BEP BEP平衡点( p r e c i s i o n = r e c a l l precision=recall precision=recall),平衡点越大,可以认为学习器更好
-
F 1 F1 F1度量: F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1=\displaystyle\frac{2\times Precision\times Recall}{Precision+Recall} F1=Precision+Recall2×Precision×Recall
- 本质是调和平均
-
F β F_{\beta} Fβ度量: F 1 = ( 1 + β 2 ) ) × P r e c i s i o n × R e c a l l ( β 2 × P r e c i s i o n ) + R e c a l l F1=\displaystyle\frac{(1+\beta^2))\times Precision\times Recall}{(\beta^2 \times Precision)+Recall} F1=(β2×Precision)+Recall(1+β2))×Precision×Recall
- 本质是加权调和平均
- β \beta β表示查全率对查准率的影响; β > 1 \beta>1 β>1说明查全率影响
-
宏F1:先计算各混淆矩阵的查全率和查准率,在平均调和
-
微F1:先计算TP FP TN FN的平均,再计算查全率、查准率和F1
-
ROC和AUC:
-
ROC(受试者工作特征曲线):
- 纵轴(真正例率): T P R = T P T P + F N TPR=\displaystyle\frac{TP}{TP+FN} TPR=TP+FNTP
- 横轴(假正例率): F P R = F P T N + F P FPR=\displaystyle\frac{FP}{TN+FP} FPR=TN+FPFP
-
AUC:ROC曲线下的面积。 A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ( y i + y i + 1 ) AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1}) AUC=21∑i=1m−1(xi+1−xi)(yi+yi+1)
-
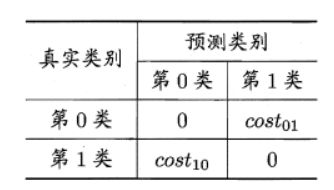
非均等代价:不同类型错误造成不同损失。
-
D + D^+ D+代表数据集 D D D的正例子集, D − D^- D−代表数据集 D D D中的反例子集,代价敏感错误率为:
E ( f ; D ; c o s t ) = 1 m ( ∑ x i ∈ D + Ⅱ ( f ( x i ) ≠ y i ) × c o s t 01 + ∑ x i ∈ D − Ⅱ ( f ( x i ) ≠ y i ) × c o s t 10 ) E(f;D;cost)=\frac{1}{m}(\sum_{x_i\in D^+}Ⅱ(f(x_i)\neq y_i)\times cost_{01}+\sum_{x_i\in D^-}Ⅱ(f(x_i)\neq y_i)\times cost_{10}) E(f;D;cost)=m1(xi∈D+∑Ⅱ(f(xi)=yi)×cost01+xi∈D−∑Ⅱ(f(xi)=yi)×cost10)
-
-
2.4 比较检验
-
统计假设检验:若在测试集上观察到学习器A比学习器B好,则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大。
-
假设检验
-
思想:根据测试错误率推估出泛化错误率的分布。
-
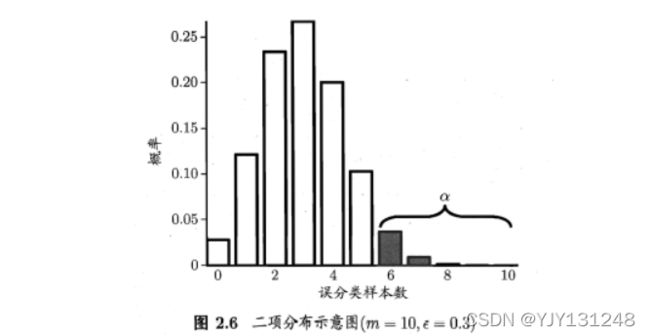
泛化错误率 ϵ \epsilon ϵ,测试错误率 ϵ ^ \hat{\epsilon} ϵ^。将 ϵ ^ × m \hat{\epsilon}\times m ϵ^×m个样本误分类的概率: P ( ϵ ^ ; ϵ ) = ( m m × ϵ ^ ) ϵ ϵ ^ × m ( 1 − ϵ ) m − ϵ ^ × m P(\hat{\epsilon};\epsilon)=\begin{pmatrix}m\\m\times \hat{\epsilon} \end{pmatrix}\epsilon^{\hat{\epsilon}\times m}(1-\epsilon)^{m-\hat{\epsilon}\times m} P(ϵ^;ϵ)=(mm×ϵ^)ϵϵ^×m(1−ϵ)m−ϵ^×m,求解导数,令一阶导数为0得到** ϵ ^ = ϵ \hat{\epsilon}=\epsilon ϵ^=ϵ**,满足二项分布。可使用二项检验,计算 ϵ ˉ \bar{\epsilon} ϵˉ(误判样本数量不少于$\epsilon_0\times m 个 样 本 的 概 率 小 于 个样本的概率小于 个样本的概率小于\alpha , 其 中 最 小 的 ,其中最小的 ,其中最小的\epsilon$):
ϵ ˉ = m i n ϵ s . t . ∑ i = ϵ 0 × m + 1 m ( m i ) ϵ i ( 1 − ϵ ) m − i < α \bar{\epsilon}=min\epsilon\space \space \space s.t.\space \space \space \sum_{i=\epsilon_0\times m+1}^m \begin{pmatrix}m\\i \end{pmatrix}\epsilon^i(1-\epsilon)^{m-i}<\alpha ϵˉ=minϵ s.t. i=ϵ0×m+1∑m(mi)ϵi(1−ϵ)m−i<α
若测试错误率 ϵ ^ < ϵ ˉ \hat{\epsilon}< \bar{\epsilon} ϵ^<ϵˉ,根据二项检验,得出结论再 α \alpha α的显著度下,假设 ϵ ≤ ϵ 0 \epsilon\le \epsilon_0 ϵ≤ϵ0不能被拒绝。
-
t检验:得到了 k k k个测试错误率, ϵ 1 ^ 、 ϵ 2 ^ 、 … 、 ϵ k ^ \hat{\epsilon_1}、\hat{\epsilon_2}、…、\hat{\epsilon_k} ϵ1^、ϵ2^、…、ϵk^,则平均错误率和方差为:
- μ = 1 k ∑ i = 1 k ϵ i ^ \mu=\frac{1}{k}\sum_{i=1}^{k}\hat{\epsilon_i} μ=k1∑i=1kϵi^
- σ = 1 k − 1 ∑ i − 1 k ( ϵ i ^ − μ ) 2 \sigma=\frac{1}{k-1}\sum_{i-1}^{k}(\hat{\epsilon_i}-\mu)^2 σ=k−11∑i−1k(ϵi^−μ)2
- t = k ( μ − ϵ 0 ) ϵ t=\displaystyle\frac{\sqrt{k}(\mu-\epsilon_0)}{\epsilon} t=ϵk(μ−ϵ0)服从自由度为 k − 1 k-1 k−1的 t t t分布。若 t t t位于 [ t − α 2 , t α 2 ] [t_{-\frac{\alpha}{2}},t_{\frac{\alpha}{2}}] [t−2α,t2α],则无法拒绝原假设。
-
-
交叉验证 t t t检验
- 两个学习器A和B,使用 k k k折交叉验证法得到测试错误率分别为 ϵ 1 A , … , ϵ k A \epsilon_1^A,…,\epsilon_k^A ϵ1A,…,ϵkA和 ϵ 1 B , … , ϵ k B \epsilon_1^B,…,\epsilon_k^B ϵ1B,…,ϵkB。计算差值 △ i = ϵ i A − ϵ i B \triangle i=\epsilon_i^A-\epsilon_i^B △i=ϵiA−ϵiB(均值应该为0)。根据$\triangle i 做 做 做t 检 验 : 检验: 检验:t=|\frac{\sqrt k\mu}{\sigma}|$
-
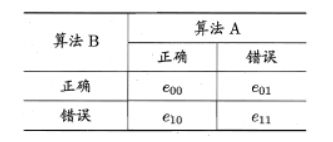
McNemar检验
- e 01 e_{01} e01和 e 10 e_{10} e10应该相等。 ∣ e 01 − e 10 ∣ |e_{01}-e_{10}| ∣e01−e10∣应服从正态分布。用卡方检验: χ 2 = ( ∣ e 01 − e 10 ∣ − 1 ) 2 e 01 + e 10 \chi ^2=\frac{(|e_{01-e_{10}}|-1)^2}{e_{01}+e_{10}} χ2=e01+e10(∣e01−e10∣−1)2服从自由度为1的卡方分布。( e 01 + e 10 e_{01}+e_{10} e01+e10通常很小,需考虑连续性校正,因此分子中有-1项)。
-
Friedman检验和Nemenyi后续检验
- 对比多组算法的性能。在多个数据集对算法进行排序,求取排序的平均值。采用F检验判断算法是否性能相同。若拒绝原假设,则采用后续检验。
2.5 偏差和方差
-
泛化误差可以分为偏差、方差和噪声之和(假定噪声期望为0)。
- 期望输出: f ˉ ( x ) = E D [ f ( x ; D ) ] \bar{f}(x)=E_D[f(x;D)] fˉ(x)=ED[f(x;D)]
- 偏差:期望输出与真实标记的差别(bias),刻画了算法本身的拟合能力。 b i a s 2 ( x ) = ( f ˉ ( x ) − y ) 2 bias^2(x)=(\bar{f}(x)-y)^2 bias2(x)=(fˉ(x)−y)2
- 使用样本数相同的不同训练集产生的方差,描述数据扰动所造成的影响。 v a r ( x ) = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] var(x)=E_D[(f(x;D)-\bar{f}(x))^2] var(x)=ED[(f(x;D)−fˉ(x))2]
- 噪声,描述了学习问题本身的难度。 ε 2 = E D [ ( y D − y ) 2 ] \varepsilon^2=E_D[(y_D-y)^2] ε2=ED[(yD−y)2]。( y D y_D yD是数据集中的标记, y y y是真实标记,即数据集中可能存在标错的情况)
- 泛化误差: E ( f ; D ) = E D [ ( f ( x ; D ) − y D ) 2 ] E(f;D)=E_D[(f(x;D)-y_D)^2] E(f;D)=ED[(f(x;D)−yD)2]
-
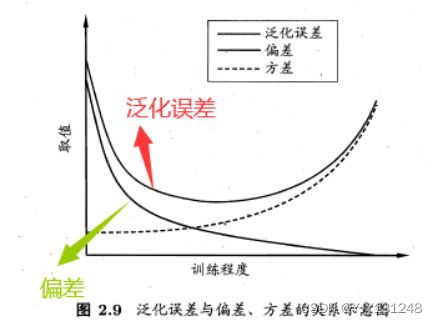
偏差-方差窘境:
- 假定能控制学习算法的训练程度。训练不足:学习器拟合能力不够强,训练数据的扰动不足以使得学习器发生显著变化,偏差主导了泛化错误率;训练程度加深,拟合能力增强,训练数据发生的扰动渐渐能被学习器学到,方差主导了泛化错误率。若训练数据自身的、非全局的特性被学习到,则将发生过拟合。
3 线性模型
3.1 基本形式
f ( x ) = w 1 x 1 + w 2 x 2 + … + w d x d + b = w T x + b f(x)=w_1x_1+w_2x_2+…+w_dx_d+b=\boldsymbol{w}^T\boldsymbol{x}+b f(x)=w1x1+w2x2+…+wdxd+b=wTx+b
3.2 线性回归
最小二乘法:基于均方误差最小化。
-
针对一元回归 f ( x i ) = w x i + b f(x_i)=wx_i+b f(xi)=wxi+b
-
原理:找到一条直线,使得所有样本到直线上的欧氏距离之和最小
( w ∗ , b ∗ ) = arg min ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 (w^*,b^*)=\mathop{\arg\min}_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\mathop{\arg\min}_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2 (w∗,b∗)=argmin(w,b)i=1∑m(f(xi)−yi)2 =argmin(w,b)i=1∑m(yi−wxi−b)2 -
参数估计:
-
求解w:
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) = 0 w = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 \frac{\partial{E_{(w,b)}}}{\partial{w}}=2(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m(y_i-b)x_i)=0\\ w=\frac{\displaystyle\sum_{i=1}^my_i(x_i-\bar{x})}{\displaystyle\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2} ∂w∂E(w,b)=2(wi=1∑mxi2−i=1∑m(yi−b)xi)=0w=i=1∑mxi2−m1(i=1∑mxi)2i=1∑myi(xi−xˉ) -
求解b:
∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) = 0 b = 1 m ∑ i = 1 m ( y i − w x i ) \frac{\partial{E_{(w,b)}}}{\partial{b}}=2(mb-\sum_{i=1}^m(y_i-wx_i))=0\\ b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i) ∂b∂E(w,b)=2(mb−i=1∑m(yi−wxi))=0b=m1i=1∑m(yi−wxi)
-
-
-
针对多元回归 f ( x ) = w x ; x = ( x ; 1 ) ; w = ( w ; 1 ) f(x)=wx;x=(x;1);w=(w;1) f(x)=wx;x=(x;1);w=(w;1)
-
原理:
w ^ ∗ = arg min w ^ ( y − X w ^ ) T ( y − X w ^ ) \hat w^*=\mathop{\arg\min}_{\hat w}(\boldsymbol{y-X\hat{w}})^T(\boldsymbol{y-X\hat{w}}) w^∗=argminw^(y−Xw^)T(y−Xw^) -
参数估计:
-
求解 w w w:
∂ E w ^ ∂ w ^ = 2 X T ( X w ^ − y ) \frac{\partial E_{\hat{w}}}{\partial{\hat{w}}}=2\boldsymbol{X^T(X\hat{w}-y)} ∂w^∂Ew^=2XT(Xw^−y)- 当 X T X X^TX XTX满秩矩阵,直接令上式为0,得 w ^ ∗ = ( X T X ) − 1 X T y \hat{w}^*=\boldsymbol{(X^TX)^{-1}X^Ty} w^∗=(XTX)−1XTy
- 当 X T X X^TX XTX不是满秩矩阵,可以解出多个 w ^ \hat{w} w^,都能使得均方误差最小化。引入正则化项(regularization)选择解。
-
-
广义线性模型: y = g − 1 ( w T x + b ) y=g^{-1}(\boldsymbol{w^Tx}+b) y=g−1(wTx+b),函数 g ( ⋅ ) g(·) g(⋅)为联系函数。
3.3 对数几率回归
对数几率函数Sigmoid函数:
y = 1 1 + e − ( w T x + b ) y=\displaystyle\frac{1}{1+e^{-(\boldsymbol{w^Tx}+b)}} y=1+e−(wTx+b)1
式(11)可变换为:
l n y 1 − y = w T x + b ln\frac{y}{1-y}=\boldsymbol{w^Tx}+b ln1−yy=wTx+b
将 y y y看作样本 x x x作为正例的可能性, 1 − y 1-y 1−y为反例的可能性,两者比值称为几率(odds),反应 x x x作为正例的相对可能性
y 1 − y \frac{y}{1-y} 1−yy
3.4 线性判别分析(LDA)
LDA线性判别分析:也叫Fisher判别分析。是一种监督降维技术。
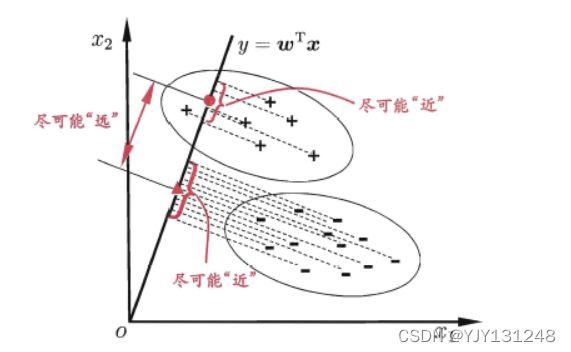
核心思想: 给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别
数学表达:极小化同类样例投影点的协方差;极大化异类样例中心之间的距离。
广 义 瑞 利 商 : J = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T ∑ 0 w + w T ∑ 1 w = w T S b w w T S w w 类 间 散 度 矩 阵 : S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T 类 内 散 度 矩 阵 : S w = ∑ 0 + ∑ 1 = ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 1 ) ( x − μ 1 ) T 广义瑞利商:J = \frac{||\boldsymbol{w^T\mu_0-w^T\mu_1}||_2^2}{\boldsymbol{w^T\sum_0w+w^T\sum_1w}}=\frac{w^TS_bw}{w^TS_ww}\\ 类间散度矩阵:S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\\ 类内散度矩阵:S_w=\sum_0+\sum_1=\sum_{\boldsymbol{x}\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum_{\boldsymbol{x}\in X_1}(x-\mu_1)(x-\mu_1)^T 广义瑞利商:J=wT∑0w+wT∑1w∣∣wTμ0−wTμ1∣∣22=wTSwwwTSbw类间散度矩阵:Sb=(μ0−μ1)(μ0−μ1)T类内散度矩阵:Sw=0∑+1∑=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T
求解 w w w: J J J与 w w w的长度无关,只与方向有关。令 w T S w w = 1 w^TS_ww=1 wTSww=1
min w − w T S b w s . t . w T S w w = 1 \mathop{\min}_{w} -w^TS_bw\\ s.t.\ \ \ w^TS_ww=1 minw−wTSbws.t. wTSww=1
由拉格朗日乘子法,后进行奇异值分解。
3.5 多分类学习
核心问题:基本思路是“拆解法”,即将多分类任务拆分为若干个二分类任务。关键在于如何对多分类任务进行拆分,以及对多个分类器进行集成。
拆分策略:
-
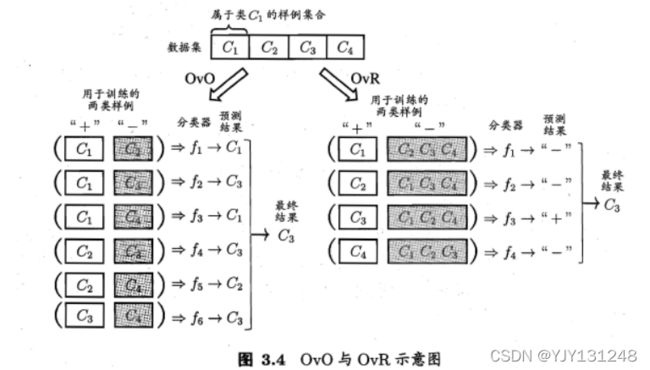
OvO(一对一):训练 N ( N − 1 ) 2 \frac{N(N-1)}{2} 2N(N−1)个分类器(两两一个),单个分类器的训练数据量较小
-
OvR(一对其余):训练 N N N个分类器,但是单个分类器训练数据较大
-
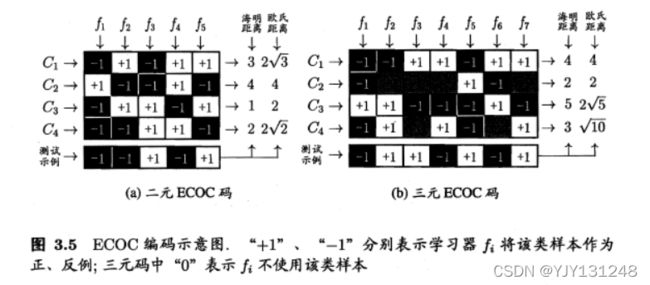
MvM(多对多):采用ECOC(纠错输出码技术)。一般来说,ECOC编码越长,纠错能力越强,开销也越大。
-
编码:划分M次(下图(a)为5次,五个分类器, f 2 f_2 f2分类器中, C 1 , C 3 C_1,C_3 C1,C3为正例)
-
解码:测试结果和各类的编码结果之间求解距离。
(a)中: 2 3 = [ − 1 − ( − 1 ) ] 2 + [ 1 − ( − 1 ) ] 2 + [ − 1 − 1 ] 2 + [ 1 − ( − 1 ) ] 2 + [ 1 − 1 ] 2 = 12 = 2 3 2\sqrt 3=\sqrt{[-1-(-1)]^2+[1-(-1)]^2+[-1-1]^2+[1-(-1)]^2+[1-1]^2}=\sqrt{12}=2\sqrt 3 23=[−1−(−1)]2+[1−(−1)]2+[−1−1]2+[1−(−1)]2+[1−1]2=12=23
-
3.6 类别不平衡问题
- 再缩放策略:一般来说阈值设置为0.5( y 1 − y = 1 \frac{y}{1-y}=1 1−yy=1)。更改分类器决策规则:若 y 1 − y > m + m _ \frac{y}{1-y}>\frac{m^+}{m^\_} 1−yy>m_m+,预测为正例。
- 前提:训练集是真是样本总体的无偏采样。这个假设很难成立,因此我们未必有效地基于训练集观测几率odds来推断真实几率
- 解决方案:
- 欠采样:去除一些反例使得正反例数目接近。
- 可能会丢失信息。
- EasyEnsemble:随机丢弃反例
- 过采样:增加一些正例使得正反例数目接近。
- 不能简单的重复样本,不然会导致过拟合。
- SMOTE:对训练集的正例进行插值得到额外的正例。
- 阈值移动:再缩放策略。
- 欠采样:去除一些反例使得正反例数目接近。