python多因素电力预测——基于LSTM神经网络
一个很简易的多因素预测电力模型,所用数据量很少,所以效果不是很好,如果数据量大,可能最后的模型精度和效果会不错,看看就行了,写的很乱(数据来源于泰迪杯最先公布的数据)。
# -*- coding: utf-8 -*-
# @Time : 2022/3/26 15:13
# @Author : 中意灬
# @FileName: 多变量.py
# @Software: PyCharm
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import r2_score
import tensorflow as tf
from tensorflow.python.keras import Sequential, layers, utils, losses
from tensorflow.python.keras.callbacks import ModelCheckpoint, TensorBoard
import warnings
def create_dataset(X, y, seq_len):
features = []
targets = []
for i in range(0, len(X) - seq_len, 1):
data = X.iloc[i:i + seq_len] # 序列数据
label = y.iloc[i + seq_len] # 标签数据
# 保存到features和labels
features.append(data)
targets.append(label)
# 返回
return np.array(features), np.array(targets)
# 3 构造批数据
def create_batch_dataset(X, y, train=True, buffer_size=1000, batch_size=128):
batch_data = tf.data.Dataset.from_tensor_slices((tf.constant(X), tf.constant(y))) # 数据封装,tensor类型
if train: # 训练集
return batch_data.cache().shuffle(buffer_size).batch(batch_size)
else: # 测试集
return batch_data.batch(batch_size)
if __name__ == '__main__':
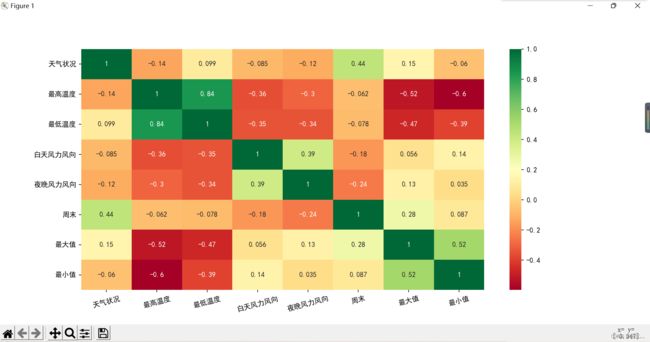
#绘制相关系数矩阵图
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False
df = pd.read_csv("C:/Users/97859/Documents/WPS Cloud Files/319911131/附件3-气象数据1.csv", encoding="GBK")
df.drop(columns='日期', axis=1, inplace=True) # 删除时间那一列
corrmat = df.astype(float).corr() # 计算相关系数
top_corr_features = corrmat.index
plt.figure()
g = sns.heatmap(df[top_corr_features].astype(float).corr(), annot=True, cmap="RdYlGn") # 绘图
plt.xticks(rotation=15)
plt.show()
plt.rcParams['font.sans-serif'] = ['SimHei']
warnings.filterwarnings('ignore')
data=pd.read_csv('附件3-气象数据1.csv',encoding='GBK',parse_dates=['日期'], index_col=['日期'])
print(data[data.isnull()==True].sum())#看看有无缺失值
'''归一化处理'''
scaler=MinMaxScaler()
data['最大值'] = scaler.fit_transform(data['最大值'].values.reshape(-1,1))
data['最小值']=scaler.fit_transform(data['最小值'].values.reshape(-1,1))
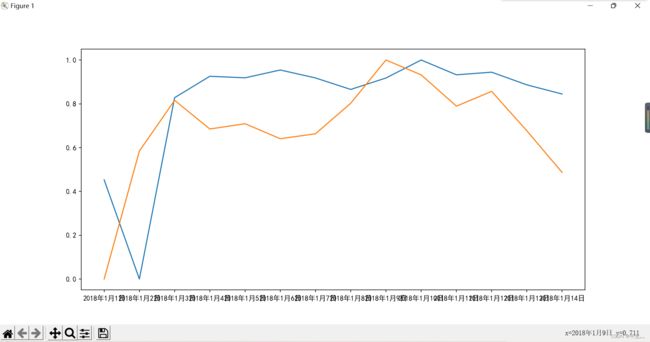
plt.figure()
plt.plot(data[['最大值','最小值']])
plt.show()
'''特征工程'''
X = data.drop(columns=['最大值','最小值'], axis=1)
y =data[['最大值','最小值']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False, random_state=666)#shuffle=false表示不打乱顺序,random_state=666表示输出的值不改变
# ① 构造训练特征数据集
train_dataset, train_labels = create_dataset(X_train, y_train, seq_len=2)
# print(train_dataset)
# ② 构造测试特征数据集
test_dataset, test_labels = create_dataset(X_test, y_test, seq_len=2)
# print(test_dataset)
# 训练批数据,未来训练快一点
train_batch_dataset = create_batch_dataset(train_dataset, train_labels)
# 测试批数据
test_batch_dataset = create_batch_dataset(test_dataset, test_labels, train=False)
# 模型搭建--版本1
model = Sequential([
layers.LSTM(units=256, input_shape=(2,6), return_sequences=True),
layers.Dropout(0.4),
layers.LSTM(units=256, return_sequences=True),
layers.Dropout(0.3),
layers.LSTM(units=128, return_sequences=True),
layers.LSTM(units=32),
layers.Dense(2)
])
# 模型编译
model.compile(optimizer='adam',loss='mse')
# 保存模型权重文件和训练日志,保持最优的那个模型
checkpoint_file = "best_model.hdf5"
checkpoint_callback = ModelCheckpoint(filepath=checkpoint_file,
monitor='loss',
mode='min',
save_best_only=True,
save_weights_only=True)
# 模型训练
history = model.fit(train_batch_dataset,
epochs=100,
validation_data=test_batch_dataset,
callbacks=[checkpoint_callback])
plt.figure()
plt.plot(history.history['loss'], label='train loss')
plt.plot(history.history['val_loss'], label='val loss')
plt.legend(loc='best')
plt.show()
'''模型预测'''
test_preds = model.predict(test_dataset, verbose=1)
plt.figure()
plt.plot(y_test, label='True')
plt.plot(test_preds, label='pred')
plt.show()
# 计算r2值,数据太少可能计算不出来
score = r2_score(test_labels, test_preds)
print("r^2 值为: ", score)
y_true = y_test[:100] # 真实值
y_pred = test_preds[:100] # 预测值
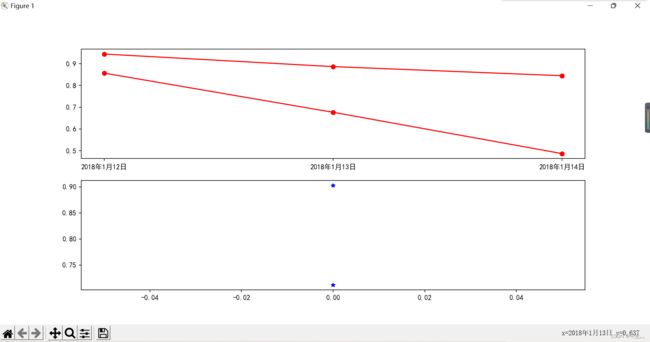
fig, axes = plt.subplots(2, 1)
axes[0].plot(y_true, marker='o', color='red')
axes[1].plot(y_pred, marker='*', color='blue')
plt.show()
#数据太少,可能计算不出来
# relative_error = 0
# '''模型精确度计算'''
# for i in range(len(y_pred)):
# relative_error += (abs(y_pred[i] - y_true[i]) / y_true[i]) ** 2
# acc = 1 - np.sqrt(relative_error / len(y_pred))
# print(f'模型的测试准确率为:', acc)运行结果:
相关性系数矩阵分析(数据是类型变量)
缺失值的查看
多因素损失值变化
计算的r^2和模型精度由于数据量太少,未能计算出来