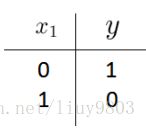深度学习之神经网络概述、BP算法
深度学习是由机器学习的神经网络发展而来的一个新的领域,模仿人脑的机制来解释数据(图像、声音和文本),结构是含多隐层的多层感知器。深度学习可以用无监督或半监督的特征学习和分层特征提取算法来高效地替代手工获取特征,通过组合低层特征形成更加抽象的高层表示属性类别或特征,以发现数据的分布式特征表示。
一、神经元
人的大脑是由大约![]() 个神经元(neuron)相互连接组成的密集网络,平均每一个神经元与其他
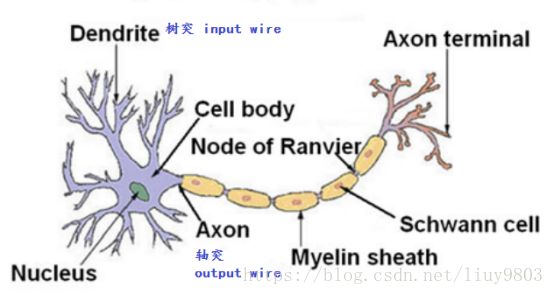
个神经元(neuron)相互连接组成的密集网络,平均每一个神经元与其他![]() 个神经元相连。神经元的树突接受其他神经元轴突传递过来的神经递质后,它自己细胞体的活性被激活或抑制;激活时细胞体内部的电位超过阈值threshold,就会通过很长的轴突向与它相连的其他神经元的树突发送神经递质。
个神经元相连。神经元的树突接受其他神经元轴突传递过来的神经递质后,它自己细胞体的活性被激活或抑制;激活时细胞体内部的电位超过阈值threshold,就会通过很长的轴突向与它相连的其他神经元的树突发送神经递质。
M-P神经元模型如下:
可以将神经元视为一个单独的决策单元,一个神经元接收到来自n个其他神经元传递过来的输入信号 ![]() ,这些输入信号通过带权重
,这些输入信号通过带权重 ![]() 的连接进行传递,神经元接收到的总输入值与神经元的阈值θ进行比较,然后通过激活函数f处理以产生神经元的输出y。
的连接进行传递,神经元接收到的总输入值与神经元的阈值θ进行比较,然后通过激活函数f处理以产生神经元的输出y。
为了统一书写格式经常将阈值写成输入中的一个偏置项bias unit:![]() ,它的权重为
,它的权重为 ![]() (
(![]() )。激活函数
)。激活函数![]() 的作用是将线性映射转换为非线性映射,常用的激活函数有sigmoid、softmax、tanh、relu、leaky relu等。
的作用是将线性映射转换为非线性映射,常用的激活函数有sigmoid、softmax、tanh、relu、leaky relu等。
神经元可以完成各种逻辑运算,这里只举几个例子:
1、逻辑与 AND
![]() ,
,![]()
![]() ,由sigmoid图像可知在(-4,4)以外的区间上它的值分别趋近于0或1:
,由sigmoid图像可知在(-4,4)以外的区间上它的值分别趋近于0或1:
![]()
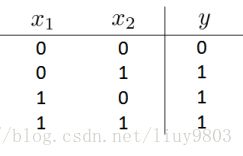
2、逻辑或 OR
![]() ,
,![]()
![]()
3、逻辑非 NOT
![]() ,
,![]()
![]() ¬
¬ ![]()
4、逻辑同或/异或非 XNOR
对线性分类器的与或非等组合,即使用多层神经元可以解决非线性可分的问题。
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ;
;![]()
![]()
二、神经网络
神经网络是具有适应性的神经元组成的广泛并行互联的网络,能够模拟生物神经系统对真实世界物体所作出的交互反映。深度神经网络DNN可理解为有很多隐藏层的神经网络,也可称为多层感知机MLP(Multi-Layer Perceptron),按层次可分为输入层input layer、任意数量的隐藏层hidden layer和输出层output layer。
1、正向传播Forward Propagation
令图中 ![]() 表示第
表示第 ![]() 层的第k个神经元,
层的第k个神经元,![]() 表示从第
表示从第 ![]() 层的第j个神经元映射到第
层的第j个神经元映射到第 ![]() 层的第i个神经元的权重,可得:
层的第i个神经元的权重,可得:
![]()
![]()
![]()
![]()
正向传播的计算过程可写为:
(1)初始化 ![]()
(2)for ![]() to 总层数L:
to 总层数L:
![]()
(3)return ![]()
2、反向传播算法 Back Propagation
BP算法是有监督学习(![]() 给定)的多层前馈神经网络用来校正模型权重矩阵的算法,由正向、反向传播两个环节组成:正向传播时x由输入层进入,正向逐层经过隐藏层传向输出层;如果输出值不满足期望,则取输出值与真实值误差的平方和作为目标函数,转入反向传播算法,反向逐层使用梯度下降更新各个神经元的权重。这两个环节反复迭代,当误差最终达到期望时,循环结束。
给定)的多层前馈神经网络用来校正模型权重矩阵的算法,由正向、反向传播两个环节组成:正向传播时x由输入层进入,正向逐层经过隐藏层传向输出层;如果输出值不满足期望,则取输出值与真实值误差的平方和作为目标函数,转入反向传播算法,反向逐层使用梯度下降更新各个神经元的权重。这两个环节反复迭代,当误差最终达到期望时,循环结束。
假设神经网络总层数为L,第![]() 层的神经元个数为
层的神经元个数为![]() ,输出结果总共有K种(K分类问题),则输出层第L层中第k类输出的误差可写为:
,输出结果总共有K种(K分类问题),则输出层第L层中第k类输出的误差可写为:
![]()
为了求出前一层第j个神经元权值 ![]() 对误差的贡献,根据复合函数求导的链式法则可得:
对误差的贡献,根据复合函数求导的链式法则可得:
其中 ![]() 为Hadamard积,即维度相同的矩阵对应位置的元素乘积
为Hadamard积,即维度相同的矩阵对应位置的元素乘积 ![]() 。令
。令![]() 表示输出层的梯度:
表示输出层的梯度:
因此第 ![]() 层的梯度
层的梯度 ![]() 可表示为:
可表示为:
得到每层的梯度后就可以使用梯度下降法更新权重矩阵了。
BP算法的流程:
输入:神经网络总层数L,各层神经元个数,激活函数,损失函数,学习率η∈(0,1),最大迭代次数maxIter及停止迭代阈值ε,m个训练样本![]() 。
。
输出:权重矩阵w
(1)随机初始化w
(2)for i =1 to maxIter:
(2-1)for i = 1 to m:
set ![]()
for ![]() ,前向传播计算
,前向传播计算 ![]()
使用损失函数计算 ![]()
for ![]() ,反向传播计算
,反向传播计算 ![]()
(2-3)如果所有权重的变化值小于停止迭代阈值ε,则停止迭代。
(3)返回权重矩阵w。
参考资料
吴恩达_机器学习PPT
https://www.cnblogs.com/pinard/p/6422831.html