混合策略改进的麻雀优化算法
文章目录
- 一、理论基础
-
- 1、麻雀优化算法
- 2、混合策略改进的麻雀优化算法
-
- (1)佳点集的种群初始化
- (2)黄金莱维飞行策略
- (3)t-分布扰动策略
- (4)动态分配侦察者策略
- (5)MI-SSA算法实现流程
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、麻雀优化算法
请参考这里。
2、混合策略改进的麻雀优化算法
(1)佳点集的种群初始化
具体原理请参考这里、这里和这里。通过对佳点集法和随机法生成二维初始种群进行对比,如图1所示。在相同的取点个数下,使用佳点集初始化方法的个体比随机初始化方法的个体更加均匀。
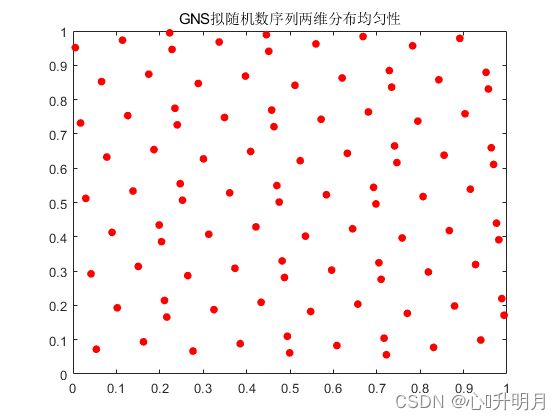
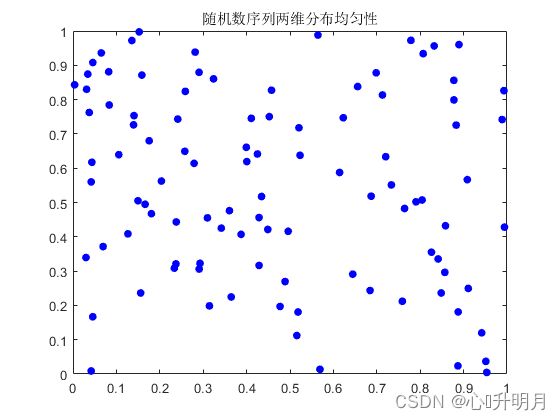
(2)黄金莱维飞行策略
莱维飞行具体原理请参考这里。其次引入正弦函数与单位圆的关系,使得发现者能遍历圆上所有位置。并且通过引入黄金分割系数缩小解空间,以便获取可能好结果的搜索区域,加快算法搜索速度。综上结合莱维飞行和黄金正弦指引机制对发现者在 R 2 < S T R_2

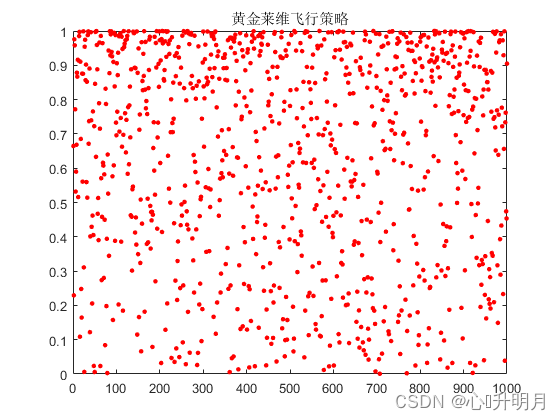
(3)t-分布扰动策略
采用t-分布扰动策略对发现者位置进行扰动,以此来提升算法的灵活性和求解效果。t-分布又称学生分布 ,含有参数自由度 n n n,当 t ( n → ∞ ) → N ( 0 , 1 ) t(n\rightarrow\infty)→N(0,1) t(n→∞)→N(0,1);当 t ( n = 1 ) = C ( 0 , 1 ) t(n=1)=C(0,1) t(n=1)=C(0,1),其中 N ( 0 , 1 ) N(0,1) N(0,1)为标准的高斯分布, C ( 0 , 1 ) C(0,1) C(0,1)为柯西分布。即t-分布的两个边界分别是高斯分布和柯西分布。引入该特性对发现者 R 2 > S T R_2>ST R2>ST的更新公式进行改进,改进公式如下: X i t + 1 = X i t + t − d i s t r i b u t i o n ( t ) ⋅ X i t (6) X_i^{t+1}=X_i^{t}+t-distribution(t)\cdot X_i^t\tag{6} Xit+1=Xit+t−distribution(t)⋅Xit(6)其中,使用当前迭代次数 t t t作为 t t t分布的自由度参数。增强算法在迭代初期的全局探索能力的同时,也加强了算法在迭代后期的局部开发能力。
(4)动态分配侦察者策略
为了挑选出更具有跳出局部极值的麻雀个体,采用了一种动态分配侦察者策略,一半的侦察者保持原有的随机挑选机制,另一半的侦察者引入竞争机制。侦察者执行侦察任务成功率越高,竞争能力越强。将竞争能力强的个体选入下一代的侦察者。令 N i , t N_{i,t} Ni,t表示第 i i i个体在 t t t代执行侦察任务的总次数, N i , s N_{i,s} Ni,s表示第 i i i个体在 t t t代成功执行侦察任务的总次数,则第 i i i个体在第 t t t代执行侦察任务的成功率 r i , t r_{i,t} ri,t为 r i , t = N i , s N i , t (7) r_{i,t}=\frac{N_{i,s}}{N_{i,t}}\tag{7} ri,t=Ni,tNi,s(7)其中, N i , s N_{i,s} Ni,s的大小取决于执行改进后侦察者位置更新公式前后适应度的比较,即若执行侦察任务后的适应度优于执行前的适应度,则该个体执行侦察任务成功,执行侦察任务的成功总次数加一,否则保持不变。
将执行侦察任务成功率进行排序,选取成功率较高的个体(占个体总数的10%)视为更具有跳出局部最优能力的个体,并且加入下一次侦察者。 X i t + 1 = { sin ( θ 3 ) ⋅ r 3 ⋅ ( X b e s t t − X i t ) + cos ( θ 4 ) ⋅ r 4 ⋅ ( X r a n d t − X i t ) if f i > f g X i t + K ⋅ ( ∣ X i t − X w o r s t t ∣ ( f i − f w ) + ε ) if f i = f g (8) X_i^{t+1}=\begin{dcases}\sin(\theta_3)\cdot r_3\cdot(X_{best}^t-X_i^t)+\cos(\theta_4)\cdot r_4\cdot(X_{rand}^t-X_i^t)\quad\text{if}\,\,f_i>f_g\\[2ex]X_i^t+K\cdot\left(\frac{|X_i^t-X_{worst}^t|}{(f_i-f_w)+\varepsilon}\right)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{if}\,\,f_i=f_g\end{dcases}\tag{8} Xit+1=⎩ ⎨ ⎧sin(θ3)⋅r3⋅(Xbestt−Xit)+cos(θ4)⋅r4⋅(Xrandt−Xit)iffi>fgXit+K⋅((fi−fw)+ε∣Xit−Xworstt∣)iffi=fg(8)其中, θ 3 \theta_3 θ3和 θ 4 \theta_4 θ4是属于 [ − π , π ] [-\pi,\pi] [−π,π]之间的随机数, r 3 r_3 r3和 r 4 r_4 r4是生均值为0、方差为1的高斯分布随机数, X r a n d t X_{rand}^t Xrandt是第 t t t代随机选择的麻雀个体。改进后的侦察者更新策略,对侦察者进行扰动,由于算法迭代初期,种群分布不均,个体位置分布差距较大,利用差分变量对侦察者进行变异,提高种群多样性;在算法迭代中后期,大多数麻雀个体不会发生太大变化,此时算法主要通过高斯分布函数系数对种群进行局部扰动,避免发生早熟。最后引入正余弦函数,动态分配权重系数,防止受单个差分变量的持续性影响。
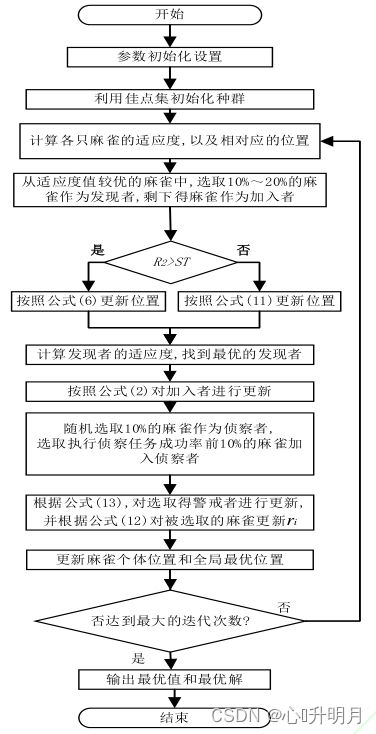
(5)MI-SSA算法实现流程
二、仿真实验与结果分析
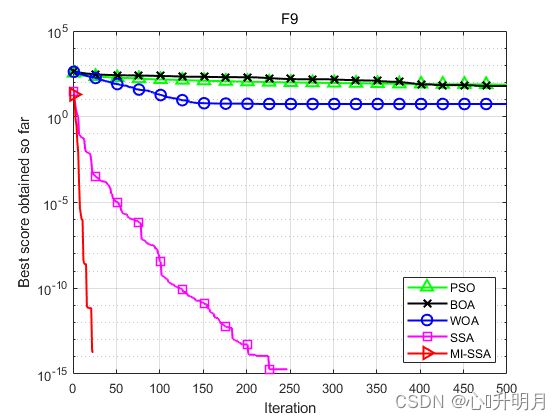
将MI-SSA与PSO、BOA、WOA和SSA进行对比,以常用23个测试函数中的F1、F2(单峰函数/30维)、F9、F10(多峰函数/30维)、F16、F18(固定维度多峰函数/2维、2维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:



函数:F1
PSO:最差值: 1.03, 最优值: 0.19502, 平均值: 0.60194, 标准差: 0.22008
BOA:最差值: 9.9276e-11, 最优值: 6.454e-11, 平均值: 7.7196e-11, 标准差: 7.7698e-12
WOA:最差值: 2.9193e-68, 最优值: 1.1971e-86, 平均值: 1.6804e-69, 标准差: 6.4467e-69
SSA:最差值: 1.2565e-37, 最优值: 7.8174e-231, 平均值: 4.2135e-39, 标准差: 2.2936e-38
MI-SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
函数:F2
PSO:最差值: 10.9291, 最优值: 2.1179, 平均值: 6.4063, 标准差: 2.0984
BOA:最差值: 3.0522e-08, 最优值: 7.8269e-09, 平均值: 2.1271e-08, 标准差: 7.7436e-09
WOA:最差值: 2.937e-50, 最优值: 3.1512e-58, 平均值: 2.4413e-51, 标准差: 7.2041e-51
SSA:最差值: 5.7198e-19, 最优值: 6.8008e-235, 平均值: 3.148e-20, 标准差: 1.1976e-19
MI-SSA:最差值: 1.0419e-195, 最优值: 2.7762e-267, 平均值: 3.4729e-197, 标准差: 0
函数:F9
PSO:最差值: 102.5482, 最优值: 45.8159, 平均值: 74.3946, 标准差: 15.9665
BOA:最差值: 206.2975, 最优值: 0, 平均值: 61.8317, 标准差: 89.2321
WOA:最差值: 165.7329, 最优值: 0, 平均值: 5.5244, 标准差: 30.2585
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
MI-SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
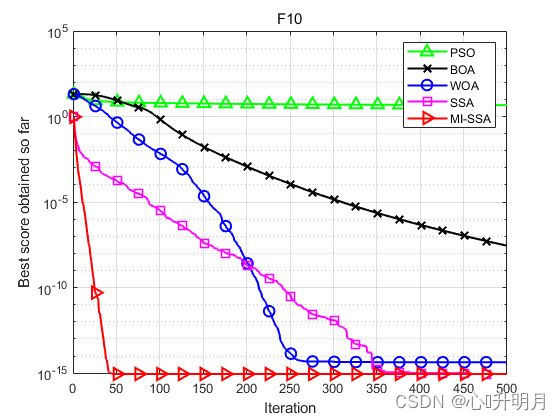
函数:F10
PSO:最差值: 8.3341, 最优值: 2.9513, 平均值: 4.6173, 标准差: 1.0161
BOA:最差值: 3.4335e-08, 最优值: 1.8341e-08, 平均值: 2.8157e-08, 标准差: 4.2674e-09
WOA:最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 4.3225e-15, 标准差: 2.7174e-15
SSA:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0
MI-SSA:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0
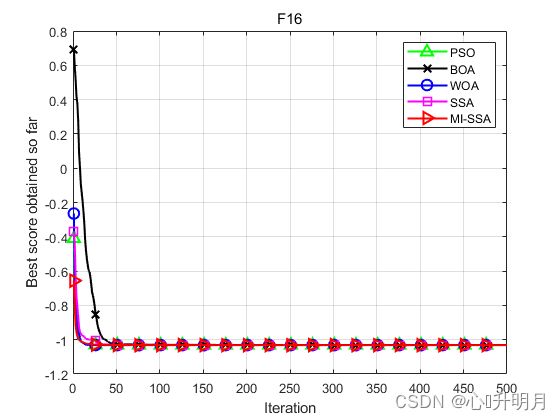
函数:F16
PSO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 2.2496e-09
BOA:最差值: -1.0293, 最优值: -1.0316, 平均值: -1.0311, 标准差: 0.00062554
WOA:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 1.8369e-09
SSA:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 5.4546e-16
MI-SSA:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 3.3854e-06
函数:F18
PSO:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 4.6744e-09
BOA:最差值: 3.1231, 最优值: 3, 平均值: 3.0277, 标准差: 0.036489
WOA:最差值: 3.0003, 最优值: 3, 平均值: 3, 标准差: 6.3965e-05
SSA:最差值: 30, 最优值: 3, 平均值: 6.6, 标准差: 9.3351
MI-SSA:最差值: 3.0003, 最优值: 3, 平均值: 3, 标准差: 5.3778e-05
实验结果表明:MI-SSA具有更好的寻优精度和收敛速度,在高维度问题求解上,具有更好的性能。
三、参考文献
[1] 陈俊, 何庆. 混合策略改进的麻雀优化算法[J/OL]. 小型微型计算机系统: 1-9 [2022-07-27].