【模型调参】【论文阅读】Bag of Tricks for Image Classification with Convolutional Neural Networks
本文根据 论文Bag of Tricks for Image Classification with Convolutional Neural Networks,总结了几种可以提高模型准确率的小技巧。
一般而言,上述的小技巧可以分为在训练过程中或对模型结构的更改 (Model Tweaks),仅少量涉及计算量的优化。
本文直接以结论的形式呈现这些技巧。
这里写目录标题
- 一些规范
-
- 可变的 learning rate
- 1 模型训练中的小技巧
-
- 1.1 Large-batch training
-
- 1.1.1 Linear scaling learning rate
- 1.1.2 Learning rate warmup
- 1.1.3 Zero γ \gamma γ
- 1.1.4 No bias decay.
- 2 模型结构的小技巧
- 3 Training Refinements
-
- 3.1 Cosine Learning Rate Decay
- 3.2 Label Smoothing
- 3.3 Mixup Training
一些规范
可变的 learning rate
learning rate 一般在训练过程中由大变小:
The learning rate is initialized to 0.1 and divided by 10 at the 30th, 60th, and 90th epochs
1 模型训练中的小技巧
1.1 Large-batch training
增加 batch size 虽然能加快训练,但是会带来如下问题:
- For convex problems, convergence rate decreases as batch size increases.
- For the same number of epochs, training with a large batch size results in a model with degraded validation accuracy compared to
the ones trained with smaller batch sizes.
上述结果告诉我们,适当减小 batch size 可以获得更快的收敛速度、更好的验证准确率。
但是,通过以下小技巧可以缓和 batch size 过大带来的危害。
1.1.1 Linear scaling learning rate
让 learning rate 和 batch size 成比例增大,可以参考公式:
In particular, if we follow He et al. [9] to choose 0.1 as the initial learning rate for batch size 256, then when changing to a larger batch size b, we will increase the initial learning rate to 0.1 × b/256.
1.1.2 Learning rate warmup
刚开始过大的 Learning rate 可能会导致收敛不稳定,因此在前几轮训练中需要逐步提高 Learning rate。
In other words, assume we will use the first m batches (e.g. 5 data epochs) to warm up, and the initial learning rate is η, then at batch i, 1 ≤ i ≤ m, we will set the learning rate to be iη/m.
1.1.3 Zero γ \gamma γ
在 ResNet 中,有一个神奇的单元叫做 residual block ,每一个 block 包含了 几个卷积层,给定一个输入 x x x, residual block 的输出为 x + b l o c k ( x ) x+block(x) x+block(x),在 b l o c k ( x ) block(x) block(x) 这一项中,block的最后一层一般是一个 batch normalization (BN) layer,先进行 standardize 得到了 x ^ \hat{x} x^,然后进行了 scale transformation 得到了 γ x ^ + β \gamma \hat{x}+\beta γx^+β, γ , β \gamma ,\beta γ,β 都是带学习的参数,如果把 γ \gamma γ 矩阵全部初始化为0,所有 residual block 会仅仅返回输入 x x x,则可以加快初始的训练速度。
1.1.4 No bias decay.
weights and bias 理论上都可以跟着 learning rate 随着训练时常衰减,但是建议仅仅让 weights 的学习率可变,bias的学习率固定比较好。
2 模型结构的小技巧
以 resnet 为例,介绍如果对模型结构进行微调。
这一部分价值不是很大,见原文。
3 Training Refinements
3.1 Cosine Learning Rate Decay
前面说到的,learning rate 的调整对训练至关重要,而且1.1.2节用到了 warmup 的技巧。
但是随着训练时间的增加,learning rate 应该适当降低,例如:
He et al. [9] decreases rate at 0.1 for every 30 epochs, we call it “step decay”. Szegedy et al. [26] decreases rate at 0.94 for every two epochs.
那么,如何衰减的比例定为多少合适呢?
In contrast to it, Loshchilov et al. [18] propose a cosine
annealing strategy. An simplified version is decreasing the learning rate from the initial value to 0 by following the cosine function. Assume the total number of batches is T (the warmup stage is ignored), then at batch t, the learning rate ηt is computed as:
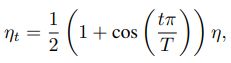
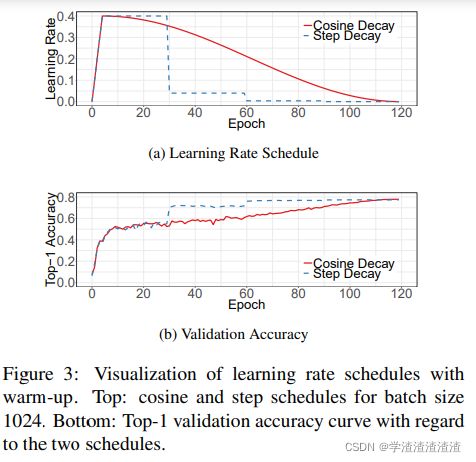
这也被称为 cosine decay,来看一下它的效果图:
3.2 Label Smoothing
见原文
3.3 Mixup Training
这种训练方式很有意思,把两个样本和他们对应的标签通过一定比例混合,生成新的样本,利用新的样本进行训练,这样貌似还可以规避训练中的隐私泄露。
