前言
上个章节中我们已经给物体加上了被选中的效果,现在可以上点交互了,这个章节主要实现的就是物体的 hover 和 click 事件,当鼠标 hover 到物体上时,我们会改变鼠标的样式使其变成移动的样子;
当 hover 到控制点时则会变成对应的操作样式;
当 click 物体时,会将物体变成激活态,也就是展示边框和控制点。话不多说,直接开撸
hover 的实现
首先我们来处理鼠标的 hover 事件,也就是 hover 到某个物体时把鼠标变成移动的样式,如果是移到激活物体的控制点上就将鼠标变成相应的旋转和缩放箭头。具体要怎么做呢?
显然 canvas 本身并不支持该功能,它就是一幅画,所有东西都被揉成可一团,所以我们是区分不了某个物体的。好在前面几个章节中我们构建了一个 Canvas 类,把所有元素都放进了 _objects 里面,现在只要从后往前遍历 _objects 数组,找出与鼠标有交集的第一个物体即可,找不到就是没有选中任何物体则将鼠标置为默认样式。之所以从后往前遍历是因为我们绘制是有顺序的,越后面添加的物体会越后面绘制,因而层级也越高,会越先被点选,所以从后往前遍历能提高效率,也符合视觉效果。
然后再提醒一下,我们物体都是有包围盒的,所以每个物体都可以简化成一个矩形,于是要判断鼠标是否 hover 到某个物体上,就变成了判断鼠标是否 hover 到某个矩形上,更进一步的就是判断点是否在矩形内部。
是不是好像有点碰撞检测的味道呢,只不过这里是点和矩形的碰撞。 显然对于一个常规的没有旋转的矩形(top、left、width、height)和一个坐标点(x, y),大家能很容易判断出来,就是 x >= left && x <= left + width && y >= top && y <= top + height 这样简单判断一下就行。那如果是个旋转之后的矩形呢?诶。。。好像不怎么好搞;
又或者是个平行四边形呢?em。。。好像也不怎么好搞;那如果是任意多边形呢?啊。。。这。。。。 我们需要一种更加通用的方式来判断点在多边形内部,这就是实打实的数学知识了。一般情况下,遇到了这种问题可以去搜一下相关解法然后 copy 过来,这里我会尽量解释的明白一些(退后,此处要开始装13了)。
- 我们知道一个多边形其实是由多条线段组成的封闭图形,相当于这个多边形将世界分成了里外两个部分,一部分在封闭区域里面,一部分在封闭区域外面。
- 现在假设我们在任意一点(鼠标坐标点),我们可以沿着该点向 x 轴方向做一条射线,然后计算出射线与多边形边的交点个数,如果交点为偶数个,则说明点在多边形外部。
- 如果交点为奇数个,则说明点在多边形内部。这个现象很有趣,大家可以在纸上试着画一下,随便画个多边形都可以,看看是不是符合上面这个规律。
可能你画了几个多边形发现这个方法确实是适用的,但是却不明白为什么我们可以用奇偶数来判断点是否在多边形内部呢?这里有个通俗易懂的解释:
- 我们可以认为在多边形的每条边上都有一个小门,经过一条边就相当于打开了一扇小门,假设我们在多边形外面,那么如果我们打开过两个小门(偶数),说明我们进去了又出来了(点在外面);
- 如果我们只打开了一个小门,说明我们出去了但没回来(点在里面)。
- 应用到实际生活中就是当你的小区被划为疫情管控区的时候,这个管控区就相当于是一个多边形,你在小区里面(多边形内)无聊了,想要出去溜达,你就必须经过一个大门(一条边),才能到达管控区外面的世界(多边形外)。哇。。。这个比喻真的是恰到好处(自己都觉得棒)。
当然聪明的同学肯定也想到了这种方法好像会有一些问题,比如:
1、点恰好在多边形上
2、射线经过多边形的顶点
3、射线与多边形的边重合 确实是这样,所以针对以上三种情况,我们还需要再加一些额外的判断条件。
- 1、对于第一点:需要判断点是否在多边形的边上,当然这种临界状态你说在里在外都可以
- 2、对于第二点:每个顶点肯定会有两条边与之相连,如果两条边在射线的同一侧,我们就算做两个交点;如果两条边分别在射线的两边,就算做一个交点。可以用极限的思想去理解,当两条边在同侧的话,取一条无限靠近该射线的水平线,显然新的水平线会和两条边都相交;而当两条边在异侧的话,同样可以取一条无限靠近该射线的水平线,显然新的水平线只会与其中一条边相交(这个思想也是真妙啊)。
- 3、对于第三点:和第二点思想差不多,采用极限思想,把这个重合的边想象成一个点即可,然后也要分与重合边相邻的两条边在同侧还是异侧两种情况。
可能你还是不懂,所以这里画了个示意图,咱们看图说话:
其实上面所说的方法有个专业的名字叫做射线检测法,它其实可以 360° 任选方向的,只不过我们通常用水平线来算,这样会比较简单点。
- 另外射线检测法还有一个最根本的原因就是射线的无穷远处一定在多边形外,这样我们才能根据交点的奇偶性来倒推位置关系。
- 数学就是这么巧妙的和前端结合起来了,一些复杂的效果归根到底还是数学的抽象。
- 不过虽然知道了大概原理,我们也不一定能写出代码来,所以这里附上一些 fabric.js 中的核心代码片段,有兴趣的可以看看(有注释的,放心食用):
class Canvas {
_initEvents() {
// 首先肯定要添加事件监听啦
Util.addListener(this.upperCanvasEl, 'mousemove', this._onMouseMove.bind(this));
}
_onMouseMove(e: MouseEvent) {
// 如果是 hover 事件,我们只需要改变鼠标样式,并不会重新渲染
const style = this.upperCanvasEl.style;
// findTarget 的过程就是看鼠标有没有 hover 到某个物体上
const target = this.findTarget(e);
// 设置鼠标样式
if (target) {
this._setCursorFromEvent(e, target);
} else {
style.cursor = this.defaultCursor;
}
}
/** 检测是否有物体在鼠标位置 */
findTarget(e: MouseEvent): FabricObject {
let target;
// 从后往前遍历所有物体,判断鼠标点是否在物体包围盒内
for (let i = this._objects.length; i--; ) {
const object = this._objects[i];
if (object && this.containsPoint(e, object)) {
target = object;
break;
}
}
if (target) return target;
}
}
class FabricObject {
/**
* 射线检测法:以鼠标坐标点为参照,水平向右做一条射线,求坐标点与多边形的交点个数
* 如果和物体相交的个数为偶数点则点在物体外部;如果为奇数点则点在内部
* 在 fabric 中的点选多边形其实就是点选矩形,所以针对矩形做了一些优化
*/
_findCrossPoints(ex: number, ey: number, lines): number {
let b1, // 射线的斜率
b2, // 边的斜率
a1,
a2,
xi, // 射线与边的交点 x
// yi, // 射线与边的交点 y
xcount = 0,
iLine; // 当前边
// 遍历包围盒的四条边
for (let lineKey in lines) {
iLine = lines[lineKey];
// 优化1:如果边的两个端点的 y 值都小于鼠标点的 y 值,则跳过
if (iLine.o.y < ey && iLine.d.y < ey) continue;
// 优化2:如果边的两个端点的 y 值都大于等于鼠标点的 y 值,则跳过
if (iLine.o.y >= ey && iLine.d.y >= ey) continue;
// 优化3:如果边是一条垂线
if (iLine.o.x === iLine.d.x && iLine.o.x >= ex) {
xi = iLine.o.x;
// yi = ey;
} else {
// 执行到这里就是一条普通斜线段了
// 用 y=kx+b 简单算下射线与边的交点即可
b1 = 0;
b2 = (iLine.d.y - iLine.o.y) / (iLine.d.x - iLine.o.x);
a1 = ey - b1 * ex;
a2 = iLine.o.y - b2 * iLine.o.x;
xi = -(a1 - a2) / (b1 - b2);
// yi = a1 + b1 * xi;
}
// 只需要计数 xi >= ex 的情况
if (xi >= ex) {
xcount += 1;
}
// 优化4:因为 fabric 中的点选只需要用到矩形,所以根据矩形的特质,顶多只有两个交点,于是就可以提前结束循环
if (xcount === 2) {
break;
}
}
return xcount;
}
}
至于物体周围的几个控制点呢,也是一样的,它们也是个矩形,所以要判断点是否在控制点内也是一样的套路一样的逻辑,这里就不展开了。
click 的实现
再来说说点选是怎么实现的,这个也很简单,和 hover 的道理如出一辙,我们能够获取到 hover 时的物体,同样也能够获取到点击时的物体,都是判断点是否在矩形内(你说巧不巧),然后将该物体的 active 属性设置为 true,其他物体设置为 false 即可,这样我们重新渲染的时候,物体会根据 active 属性自动调用 drawBorders 和 drawControls 方法,看起来物体就被选中了,注意 hover 的时候不会导致重绘,只改变鼠标样式;
点选会导致重绘并改变鼠标样式。另外我们还可以对点选进行一些优化,比如记录最近一个激活的物体,然后点选的时候先判断鼠标点是否在最近一个激活物体的内部,如果在,就可以省去遍历的过程了。
矩形的坐标哪来的
其实上面的讲解我特意漏说了一个点,就是包围盒和控制点的那个矩形是怎么来的,目前我们只是单纯的画出了边框和控制点,但是并没有记录它们的宽高和位置,所以现在我们需要在初始化物体的时候进行一些简单计算并用变量 oCoords 保存起来,就像这样:
export interface Coords {
/** 左上控制点 */
tl: Coord;
/** 右上控制点 */
tr: Coord;
/** 右下控制点 */
br: Coord;
/** 左下控制点 */
bl: Coord;
/** 左中控制点 */
ml: Coord;
/** 上中控制点 */
mt: Coord;
/** 右中控制点 */
mr: Coord;
/** 下中控制点 */
mb: Coord;
/** 上中旋转控制点 */
mtr: Coord;
}
class Canvas {
_initObject(obj: FabricObject) {
obj.setCoords(); // 记录控制点位置和大小,其实就是各个矩形的顶点坐标
obj.canvas = this;
}
}
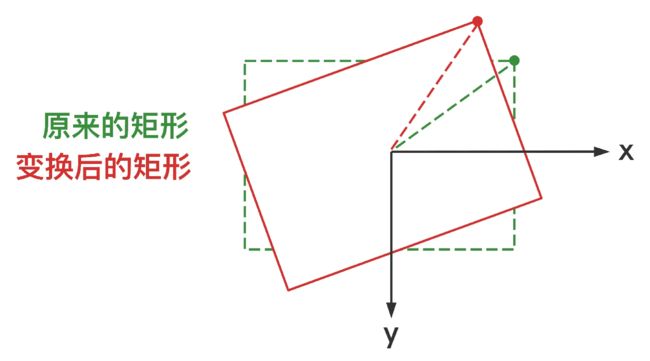
具体计算方法比较繁琐,我就不贴上来了,有兴趣的可以去看看源码,这里就简单放个图:
以上图的矩形为例子,其实就是算出上图矩形四个顶点的位置,写的时候你只需要考虑一个点(比如图中右上角的顶点)是怎么算的就行,其他点都是一样的,相信你慢慢算一定可以算出来的。
当然如果物体的某些属性改变了,比如物体经过变换,记得需要及时更新 oCoords 的值。
点在多边形内的其他判断方法
其实判断点是否在多边形内部还有其他方法,比如:
- 用 canvas 自身的 api
isPointInPath - 将多边形切割成多个三角形,然后判断点是否在某个三角形内部
- 转角累加法
- 面积法
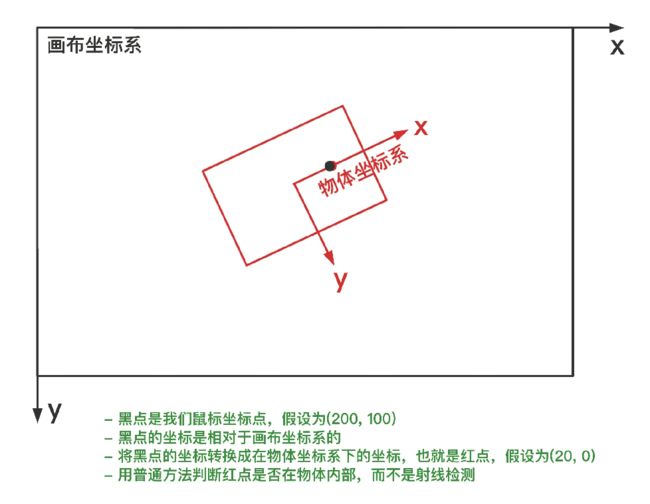
... 这里我稍微说下另一种比较有意思的方法,如果不理解射线检测法的同学,我们还能这么搞:假设矩形旋转了一定角度,那我们将鼠标坐标点也旋转一下,这样旋转后的坐标点就不就又和矩形是同一个水平垂直方向吗,就像下图这样:
上述方法的核心要点就是将鼠标点换算成物体自身坐标系下的点(写成矩阵的形式会比较方便点),然后再用原始的方法判断即可,是不是看起来也挺方便的样子。
穿透
现在我们来扩充下另外一个知识点,就是目前我们点选物体的时候,其实是点选包围盒,当点到物体四周空白区域的时候,物体也是会被选中的,如果不想把空白区域也算在物体的点击范围内(比如 png 图片),那该怎么做呢?
这个东西挺有意思的,可以停个几秒种,思考一下下。。。。 显然我们要在上文所说的 findTarget 中做文章,除了判断点是否在包围盒内,还要进一步判断点击的是不是空白的地方,所谓空白,一定程度上可以理解成是透明的地方。
于是这就要用到前几个章节提到过的第三个画布 cacheCanvasEl 缓存画布,在点击到了包围盒之后我们还需要把这个物体画到这个缓存画布上,然后用 getImageData 来获取鼠标位置所在点的像素信息,当然我们允许有误差,所以会取这个鼠标点周围的一小块正方形的像素信息,接着遍历每个像素,如果找到一个像素中 rgba 的 a 的值 > 0 就说明至少有一个颜色存在,亦即不透明,退出循环,否则就是透明的,最后清除 getImageData 变量,清除缓冲层画布即可。
是不是有种豁然开朗的感觉,有了思路,代码实现起来就比较简单了:
class Canvas {
/**
* 用缓冲层判断物体是否透明,目前默认都是不透明,可以加一些参数属性,比如允许有几个像素的误差
* @param {FabricObject} target 物体
* @param {number} x 鼠标的 x 值
* @param {number} y 鼠标的 y 值
* @param {number} tolerance 允许鼠标的误差范围
* @returns
*/
_isTargetTransparent(target: FabricObject, x: number, y: number, tolerance: number = 0) {
// 1、在缓冲层绘制物体
// 2、通过 getImageData 获取鼠标位置的像素数据信息
// 3、遍历像素数据,如果找到一个 rgba 中的 a 的值 > 0 就说明至少有一个颜色,亦即不透明,退出循环
// 4、清空 getImageData 变量,并清除缓冲层画布
let cacheContext = this.contextCache;
this._draw(cacheContext, target);
if (tolerance > 0) { // 如果允许误差
if (x > tolerance) {
x -= tolerance;
} else {
x = 0;
}
if (y > tolerance) {
y -= tolerance;
} else {
y = 0;
}
}
let isTransparent = true;
let imageData = cacheContext.getImageData(x, y, tolerance * 2 || 1, tolerance * 2 || 1);
for (let i = 3; i < imageData.data.length; i += 4) { // 只要看第四项透明度即可
let temp = imageData.data[i];
isTransparent = temp <= 0;
if (isTransparent === false) break; // 找到一个颜色就停止
}
imageData = null;
this.clearContext(cacheContext);
return isTransparent;
}
}
怎么样,这个方法看起来还是有点意思的,而且通俗易懂。
当然了,这对不同物体可以有不同的检测方法:
比如物体是一个几何图形,假设是正多边形,同样的,我们希望选中的是正多边形,而不是正多边形包围盒所形成的的矩形,这时候只需要把点选物体包围盒的逻辑改成点选正多边形的逻辑即可,同样采用的是射线检测法(怎么又绕回来了);
如果物体是条线段,就变成了点是否在线上的检测;
如果是个圆,那就更简单了,诸如此类。。。
此外还有一种空间换时间的取巧方法,就是在创建物体的时候在离屏 canvas 上多绘制一个和这个物体形状大小一样的纯色物体,画布上的物体都有各自的颜色并且唯一,然后做一个 { color: object } 的映射,之后我们点选的时候主要是通过点击坐标获取到对应离屏 canvas 上的纯颜色,再根据映射取出对应的物体即可,这也是一种方法。
本章小结
这个章节我们主要实现了如何处理物体的 hover 和 click 事件,本质其实就是如何如何判断一个点在多边形内部,你可能听过一些方法,但不知道实际开发时是怎么应用上的,希望读完本章你能记得射线检测法的应用,它的核心就是越过一条边里外两个世界就会互相交换。然后这里是简版 fabric.js 的代码链接,有兴趣的可以看看。好啦,本次分享就到这里,有什么问题欢迎点赞评论留言,我们下期再见,拜拜
canvas 中物体边框和控制点的实现(四)
实现一个轻量 fabric.js 系列三(物体基类)
实现一个轻量 fabric.js 系列二(画布初始化)
实现一个轻量 fabric.js 系列一(摸透 canvas)
以上就是JS前端使用canvas实现物体的点选示例的详细内容,更多关于JS前端canvas物体点选的资料请关注脚本之家其它相关文章!