深度学习模型压缩与加速技术(二):参数量化
目录
-
-
- 总结
- 参数量化
-
- 参数量化定义
- 参数量化特点
- 1.二值化
-
- 二值化权重
- 二值化权重与激活函数
- 2.三值化
- 3.聚类量化
- 4.混合位宽
-
- 手工固定
- 自主确定
- 训练技巧
- 参考文献
-
深度学习模型的压缩和加速是指利用神经网络参数的冗余性和网络结构的冗余性精简模型,在不影响任务完成度的情况下,得到参数量更少、结构更精简的模型。被压缩后的模型计算资源需求和内存需求更小,相比原始模型能够满足更加广泛的应用需求。在深度学习技术日益火爆的背景下,对深度学习模型强烈的应用需求使得人们对内存占用少、计算资源要求低、同时依旧保证相当高的正确率的“小模型”格外关注。利用神经网络的冗余性进行深度学习的模型压缩和加速引起了学术界和工业界的广泛兴趣,各种工作也层出不穷。
本文参考2021发表在软件学报上的《深度学习模型压缩与加速综述》进行了总结和学习。
相关链接:
深度学习模型压缩与加速技术(一):参数剪枝
深度学习模型压缩与加速技术(二):参数量化
深度学习模型压缩与加速技术(三):低秩分解
深度学习模型压缩与加速技术(四):参数共享
深度学习模型压缩与加速技术(五):紧凑网络
深度学习模型压缩与加速技术(六):知识蒸馏
深度学习模型压缩与加速技术(七):混合方式
总结
| 模型压缩与加速技术 | 描述 |
|---|---|
| 参数剪枝(A) | 设计关于参数重要性的评价准则,基于该准则判断网络参数的重要程度,删除冗余参数 |
| 参数量化(A) | 将网络参数从 32 位全精度浮点数量化到更低位数 |
| 低秩分解(A) | 将高维参数向量降维分解为稀疏的低维向量 |
| 参数共享(A) | 利用结构化矩阵或聚类方法映射网络内部参数 |
| 紧凑网络(B) | 从卷积核、特殊层和网络结构3个级别设计新型轻量网络 |
| 知识蒸馏(B) | 将较大的教师模型的信息提炼到较小的学生模型 |
| 混合方式(A+B) | 前几种方法的结合 |
A:压缩参数 B:压缩结构
参数量化
参数量化定义
参数量化是指用较低位宽表示 32 位浮点网络参数,网络参数包括权重、激活值、梯度和误差等等,可以使用统一的位宽(如16-bit、8-bit、2-bit 和 1-bit 等),也可以根据经验或一定策略自由组合不同的位宽
参数量化特点
-
优点:
- 能够显著减少参数存储空间与内存占用空间,将参数从 32 位浮点型量化到 8 位整型,从而缩小 75%的存储空间,这对于计算资源有限的边缘设备和嵌入式设备进行深度学习模型的部署和使用都有很大的帮助;
- 能够加快运算速度,降低设备能耗,读取 32 位浮点数所需的带宽可以同时读入4个8位整数,并且整型运算相比浮点型运算更快,自然能够降低设备功耗。
-
缺点:
- 网络参数的位宽减少损失了一部分信息量,会造成推理精度的下降,虽然能够通过微调恢复部分精确度,但也带来时间成本的增加;
- 量化到特殊位宽时,很多现有的训练方法和硬件平台不再适用,需要设计专用的系统架构,灵活性不高。
1.二值化
二值化是指限制网络参数取值为 1 或-1,极大地降低了模型对存储空间和内存空间的需求,并且将原来的乘法操作转化成加法或者移位操作,显著提高了运算速度,但同时也带来训练难度和精度下降的问题。
二值化权重
- Courbariaux 等人[56]提出了 Binaryconnect,将二值化策略用于前向计算和反向传播,但在使用随机梯度更新法(SGD)更新参数时,仍需使用较高位宽。
- Hou 等人[57]提出一种直接考虑二值化权重对 loss 产生影响的二值化算法,采用对角海森近似的近似牛顿算法得到二值化权重。
- Xu 等人[58]提出局部二值卷积(LBC) 来替代传统卷积,LBC 由一个不可学习的预定义 filter、一个非线性激活函数和一部分可以学习的权重组成,其组合达到与激活的传统卷积 filter 相同的效果。
- Guo 等人[59]提出了 Network sketching 方法,使用二值权重共享的卷积,即,对于同层的卷积运算(即拥有相同输入),保留前一次卷积的结果,卷积核的相同部分直接复用结果。
- McDonnell 等人[60]将符号函数作为实现二值化的方法。
- Hu等人[61]通过哈希将数据投影到汉明空间,将学习二值参数的问题转化为一个在内积相似性下的哈希问题。
二值化权重与激活函数
- Courbariaux 等人[62]首先提出了 Binarized neural network(BNN),将权重和激活值量化到±1。
- Rastegari 等人[63]在文献[62]的基础上提出了Xnor-net,将卷积通过 xnor 和位操作实现,从头训练一个二值化网络。
- Li 等人[64]在 Xnor-net[63]的基础上改进其激活值量化,提出了 High-order residual quantization(HORQ) 方法。
- Liu 等人[65]提出了 Bi-real net,针对Xnor-net[63]进行网络结构改进和训练优化
- Lin 等人[66]提出了 ABC-Net,用多个二值操作加权来拟合卷积操作.
2.三值化
三值化是指在二值化的基础上引入 0 作为第 3 阈值,减少量化误差。
- Li 等人[67]提出了三元权重网络 TWN,将权重量化为{-w,0,+w}。
- 不同于传统的1或者权重均值,Zhu 等人[68]提出了 Trained ternary quantization(TTQ),使用两个可训练的全精度放缩系数,将权重量化到{ − w n -w_n −wn,0, w p w_p wp},权重不对称使网络更灵活。
- Achterhold 等人[69]提出了 Variational network quantization(VNQ),将量化问题形式化为一个变分推理问题。引入量化先验,最后可以用确定性量化值代替权值。
3.聚类量化
当参数数量庞大时,可利用聚类方式进行权重量化。
-
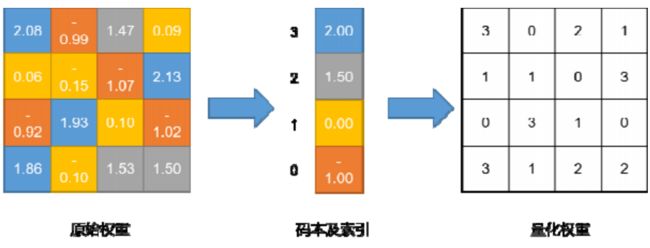
Gong 等人[70]最早提出将 k-means 聚类用于量化全连接层参数,如图所示,对原始权重聚类形成码本,为权值分配码本中的索引,所以只需存储码本和索引,无需存储原始权重信息。
-
Wu 等人[71]将 k-means 聚类拓展到卷积层,将权值矩阵划分成很多块,再通过聚类获得码本,并提出一种有效的训练方案抑制量化后的多层累积误差。
-
Choi 等人[72]分析了量化误差与 loss 的定量关系,确定海森加权失真测度是量化优化的局部正确目标函数,提出了基于海森加权 k-means 聚类的量化方法。
-
Xu 等人[73]提出了分别针对不同位宽的 Single-level network quantization(SLQ) 和 Multi-level network quantization(MLQ) 两种方法,SLQ 方法针对高位宽,利用 k-means 聚类将权重分为几簇,依据量化 loss,将簇分为待量化组和再训练组,待量化组的每个簇用簇内中心作为共享权重,剩下的参数再训练。而 MLQ 方法针对低位宽,不同于 SLQ 方法一次量化所有层,MLQ 方法采用逐层量化的方式。
4.混合位宽
手工固定
由于二值网络会降低模型的表达能力,研究人员提出,可以根据经验手工选定最优的网络参数位宽组合。
- Lin 等人[74]在 BNN[62]的基础上,提出把 32-bit 权重概率性地转换为二元和三元值的组合。
- Zhou 等人[75]提出了DoReFa-Net,将权重和激活值分别量化到1-bit 和 2-bit。
- Mishra 等人[76]提出了 WRPN,将权重和激活值分别量化到 2-bit 和 4-bit
- Köster 等人[77]提出的 Flexpoint 向量有一个可动态调整的共享指数,证明 16 位尾数和 5 位共享指数的 Flexpoint 向量表示在不修改模型及其超参数的情况下,性能更优。
- Wang 等人[78]使用 8 位浮点数进行网络训练,部分乘积累加和权重更新向量的精度从 32-bit 降低到 16-bit,达到与 32-bit 浮点数基线相同的精度水平。除了权重和激活值,研究者们将梯度和误差也作为可优化的因素。这些同时考虑了权重、激活值、梯度和误差的方法的量化位数和特点对比可见下表,表中的 W、A、G 和 E 分别代表权重、激活值、梯度和误差
| 方法 | W | A | G | E | 特点 |
|---|---|---|---|---|---|
| [79] | 16 | 32 | 32 | 32 | 引入随机舍入技术 |
| [81] | 32 | 8 | 8 | 32 | 加速数据传输,提高并行训练的性能 |
| [82] | 8 | 8 | 32 | 32 | 仅测试时使用整数运算 |
| [83] | 8 | 8 | 8 | 32 | 计算梯度的最后一个步骤保留更高精度 |
| [84] | 2 | 8 | 8 | 8 | 离散训练和推理 |
自主确定
由于手工确定网络参数位宽存在一定的局限性,可以设计一定的策略,以帮助网络选择合适的位宽组合。
- Khoram 等人[18]迭代地使用 loss 的梯度来确定每个参数的最优位宽,使得只有对预测精度重要的参数才有高精度表示。
- Wang 等人[84]提出两步量化方法:先量化激活值再量化权重.针对激活值量化,提出了稀疏量化方法。对于权重量化,将其看成非线性最小二乘回归问题。
- Faraone 等人[85]提出了基于梯度的对称量化方法 SYQ,设计权值二值化或三值化,并在 pixel 级别、row 级别和 layer 级别定义不同粒度的缩放因子以估计网络权重;至于激活值,则量化为 2-bit 到 8-bit 的定点数。
- Zhang 等人[86]提出了 Learned quantization(LQ-nets),使量化器可以与网络联合训练,自适应地学习最佳量化位宽。
训练技巧
由于量化网络的网络参数不是连续的数值,所以不能像普通的卷积神经网络那样直接使用梯度下降方法进行训练,而需要特殊的方法对这些离散的参数值进行处理,使其不断优化,最终实现训练目。
- Zhou 等人[87]提出了一种增量式网络量化方法 INQ。先对权重进行划分,将对预测精度贡献小的权重划入量化组;然后通过再训练恢复性能。
- Cai 等人[88]提出了 Halfwave Gaussian quantizer(HWGQ) 方法,设计了两个 ReLU 非线性逼近器(前馈计算中的半波高斯量化器和反向传播的分段连续函数),以训练低精度的深度学习网络。
- Leng 等人[89]提出,利用ADMM[90]解决低位宽网络训练问题。
- Zhuang 等人[91]针对低位宽卷积神经网络提出 3 种训练技巧,以期得到较高精度。
- Zhou 等人[92]提出一种显式的 loss-error-aware 量化方法,综合考虑优化过程中的 loss 扰动和权值近似误差,采用增量量化策略。
- Park 等人[93]提出了价值感知量化方法来降低训练中的内存成本和推理中的计算/内存成本,并且提出一种仅在训练过程中使用量化激活值的量化反向传播方法。
- Shayer 等人[94]展示了如何通过对局部再参数化技巧的简单修改,来实现离散权值的训练,该技巧以前用于训练高斯分布权值。
- Louizos 等人[95]引入一种可微的量化方法,将网络的权值和激活值的连续分布转化为量化网格上的分类分布,随后被放宽到连续代理,可以允许有效的基于梯度的优化。
参考文献
主要参考:高晗,田育龙,许封元,仲盛.深度学习模型压缩与加速综述[J].软件学报,2021,32(01):68-92.DOI:10.13328/j.cnki.jos.006096.
[56] Courbariaux M, Bengio Y, David JP. Binaryconnect: Training deep neural networks with binary weights during propagations. In: Advances in Neural Information Processing Systems. 2015. 31233131.
[57] Hou L, Yao Q, Kwok JT. Loss-aware binarization of deep networks. arXiv Preprint arXiv: 1611.01600, 2016.
[58] Juefei-Xu F, Naresh Boddeti V, Savvides M. Local binary convolutional neural networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 1928.
[59] Guo Y, Yao A, Zhao H, et al. Network sketching: Exploiting binary structure in deep CNNs. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 59555963.
[60] McDonnell MD. Training wide residual networks for deployment using a single bit for each weight. arXiv Preprint arXiv: 1802. 08530, 2018.
[61] Hu Q, Wang P, Cheng J. From hashing to CNNs: Training binary weight networks via hashing. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. 2018.
[62] Courbariaux M, Hubara I, Soudry D, et al. Binarized neural networks: Training deep neural networks with weights and activations constrained to+ 1 or 1. arXiv Preprint arXiv: 1602.02830, 2016.
[63] Rastegari M, Ordonez V, Redmon J, et al. Xnor-net: Imagenet classification using binary convolutional neural networks. In: Proc. of the European Conf. on Computer Vision. Cham: Springer-Verlag, 2016. 525542.
[64] Li Z, Ni B, Zhang W, et al. Performance guaranteed network acceleration via high-order residual quantization. In: Proc. of the IEEE Int’l Conf. on Computer Vision. 2017. 25842592.
[65] Liu Z, Wu B, Luo W, et al. Bi-real net: Enhancing the performance of 1-bit CNNs with improved representational capability and advanced training algorithm. In: Proc. of the European Conf. on Computer Vision (ECCV). 2018. 722737.
[66] Lin X, Zhao C, Pan W. Towards accurate binary convolutional neural network. In: Advances in Neural Information Processing Systems. 2017. 345353.
[67] Li F, Zhang B, Liu B. Ternary weight networks. arXiv Preprint arXiv: 1605.04711, 2016.
[68] Zhu C, Han S, Mao H, et al. Trained ternary quantization. arXiv Preprint arXiv: 1612.01064, 2016.
[69] Achterhold J, Koehler J M, Schmeink A, et al. Variational network quantization. In: Proc. of the ICLR 2017. 2017.
[70] Gong Y, Liu L, Yang M, et al. Compressing deep convolutional networks using vector quantization. arXiv Preprint arXiv: 1412. 6115, 2014.
[71] Wu J, Leng C, Wang Y, et al. Quantized convolutional neural networks for mobile devices. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2016. 48204828.
[72] Choi Y, El-Khamy M, Lee J. Towards the limit of network quantization. arXiv Preprint arXiv: 1612.01543, 2016.
[73] Xu Y, Wang Y, Zhou A, et al. Deep neural network compression with single and multiple level quantization. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. 2018.
[74] Lin Z, Courbariaux M, Memisevic R, et al. Neural networks with few multiplications. arXiv Preprint arXiv: 1510.03009, 2015.
[75] Zhou S, Wu Y, Ni Z, et al. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv Preprint arXiv: 1606.06160, 2016.
[76] Mishra A, Nurvitadhi E, Cook JJ, et al. WRPN: Wide reduced-precision networks. arXiv Preprint arXiv: 1709.01134, 2017.
[77] Köster U, Webb T, Wang X, et al. Flexpoint: An adaptive numerical format for efficient training of deep neural networks. In: Advances in Neural Information Processing Systems. 2017. 17421752.
[78] Wang N, Choi J, Brand D, et al. Training deep neural networks with 8-bit floating point numbers. In: Advances in Neural Information Processing Systems. 2018. 76757684.
[79] Gupta S, Agrawal A, Gopalakrishnan K, et al. Deep learning with limited numerical precision. In: Proc. of the Int’l Conf. on Machine Learning. 2015. 17371746.
[80] Dettmers T. 8-bit approximations for parallelism in deep learning. arXiv Preprint arXiv: 1511.04561, 2015.
[81] Jacob B, Kligys S, Chen B, et al. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 27042713.
[82] Banner R, Hubara I, Hoffer E, et al. Scalable methods for 8-bit training of neural networks. In: Advances in Neural Information Processing Systems. 2018. 51455153.
[83] Wu S, Li G, Chen F, et al. Training and inference with integers in deep neural networks. arXiv Preprint arXiv: 1802.04680, 2018.
[84] Wang P, Hu Q, Zhang Y, et al. Two-step quantization for low-bit neural networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 43764384.
[85] Faraone J, Fraser N, Blott M, et al. SYQ: Learning symmetric quantization for efficient deep neural networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 43004309.
[86] Zhang D, Yang J, Ye D, et al. LQ-nets: Learned quantization for highly accurate and compact deep neural networks. In: Proc. of the European Conf. on Computer Vision (ECCV). 2018. 365382.
[87] Zhou A, Yao A, Guo Y, et al. Incremental network quantization: Towards lossless CNNs with low-precision weights. arXiv Preprint arXiv: 1702.03044, 2017.
[88] Cai Z, He X, Sun J, et al. Deep learning with low precision by half-wave Gaussian quantization. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 59185926.
[89] Leng C, Dou Z, Li H, et al. Extremely low bit neural network: Squeeze the last bit out with ADMM. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. 2018.
[90] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 2011,3(1):1122.
[91] Zhuang B, Shen C, Tan M, et al. Towards effective low-bitwidth convolutional neural networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 79207928.
[92] Zhou A, Yao A, Wang K, et al. Explicit loss-error-aware quantization for low-bit deep neural networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 94269435.
[93] Park E, Yoo S, Vajda P. Value-Aware quantization for training and inference of neural networks. In: Proc. of the European Conf.on Computer Vision (ECCV). 2018. 580595.
[94] Shayer O, Levi D, Fetaya E. Learning discrete weights using the local reparameterization trick. arXiv Preprint arXiv: 1710.07739, \2017.
[95] Louizos C, Reisser M, Blankevoort T, et al. Relaxed quantization for discretized neural networks. arXiv Preprint arXiv: 1810.01875, 2018.