带花树,Edmonds's matching algorithm,一般图最大匹配
看了两篇博客,觉得写得不错,便收藏之。。
首先是第一篇,转自某Final牛
带花树……其实这个算法很容易理解,但是实现起来非常奇葩(至少对我而言)。
比如昨晚找到一篇鄙视带花树的论文,然后介绍了一种O(E)的一般图最大匹配……我以为找到了神论文,然后ACM_DIY众神纷纷表示这个是错的……于是神论文成为了”神论文“……
又比如围观nocow上带花树标程,一看……这显然是裸的匈牙利算法……货不对板啊
当然……如果二分图的匈牙利算法还不会请先围观求二分图最大匹配的匈牙利算法。
实际上任意图求最大匹配也是找增广路,但是由于奇环的出现,找增广路变得困难。
首先明确一点,增广路上是不能有重复出现的点的。

二分图中,匹配边可以看作是有向的,比如定义总是从X集指向Y集。假若定义了起点必须在X集中,那么增广路中出现该匹配边时,必然是按照这个方向的。所以一个点在增广路中的奇偶性是确定的。
而这个图中,从增广路3->1->4->5和2->4->1->6可以看出,对于有奇环的任意图,1和4这两个点在增广路中所在位置的奇偶性不再一定。于是我们考虑处理这些奇环。
定义奇环:包含2k+1个点和k条匹配边的一个环。(如果不是这样,我们找增广路不会走上去)
对于这个奇环,k条匹配覆盖了2k个点,那么显然有一个点未被覆盖。我们拿出这个点来讨论。
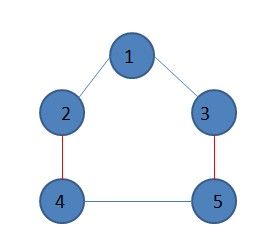
比如图中的1号点就是这个这个特殊的点。除了这个点以外,其它的点都被覆盖了,所以只能向外连非匹配边,而1号点可以向外连匹配边
或非匹配边。
如果1号点没有被外面的点匹配,那么无论从其它的哪个点走进来,都能以1为终点找到增广路。(要么顺时针跑到1,要么逆时针)
同理如果1号点被外面的点匹配了,那么无论从其它的哪个点走进来,都能把这个圈看成一个点,然后从1的那条匹配边穿出去。(要么顺时针,要么逆时针)
于是这个奇环就可以看成一个点,其主要特性由1号点体现(诸如和谁匹配了之流)。
这个合成点就叫做花。这个算法的思想就是不断地把奇环合成点,直至找到增广路(合成了某朵花以后就把整朵花当成一个点)。
考虑用BFS搜索增广路。
围观wiki这个图

由于BFS的性质,我们找到奇环只能是和同层的点,或者下下一层的点。
然后奇环的关键点必然是这棵BFS树里深度最浅的点。然后考虑合成以后,花如何展开对应的路径,使得我们能够增广。
花套花这个东西想起来都纠结>_<。
amber的程序里面并没有把点真的合成,只是弄了一个表示集合的标号:Base,然后邻接矩阵就不用变来变去了。
对于花中连向父亲的是匹配边的点,他的增广路显然是直接顺着父亲走,而如果连向父亲的边是非匹配边的点,那么显然是往后走然后跑过红色的横插边,然后再向上跑回关键点。
注意到如果连向父子的边是匹配边的点原先是不需要Father这个域来描述的,直接用表示匹配的那个域就可以了。但是现在在花中,他的Father这个域就要起作用了,用来向后指向,然后绕过红色横插边然后再跑回关键点。
 实在是太精妙了。
实在是太精妙了。
1 //Problem:http://acm.timus.ru/problem.aspx?space=1&num=1099 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <iostream> 6 #include <algorithm> 7 using namespace std; 8 const int N=250; 9 int n; 10 int head; 11 int tail; 12 int Start; 13 int Finish; 14 int link[N]; //表示哪个点匹配了哪个点 15 int Father[N]; //这个就是增广路的Father……但是用起来太精髓了 16 int Base[N]; //该点属于哪朵花 17 int Q[N]; 18 bool mark[N]; 19 bool map[N][N]; 20 bool InBlossom[N]; 21 bool in_Queue[N]; 22 23 void CreateGraph(){ 24 int x,y; 25 scanf("%d",&n); 26 while (scanf("%d%d",&x,&y)!=EOF) 27 map[x][y]=map[y][x]=1; 28 } 29 30 void BlossomContract(int x,int y){ 31 fill(mark,mark+n+1,false); 32 fill(InBlossom,InBlossom+n+1,false); 33 #define pre Father[link[i]] 34 int lca,i; 35 for (i=x;i;i=pre) {i=Base[i]; mark[i]=true; } 36 for (i=y;i;i=pre) {i=Base[i]; if (mark[i]) {lca=i; break;} } //寻找lca之旅……一定要注意i=Base[i] 37 for (i=x;Base[i]!=lca;i=pre){ 38 if (Base[pre]!=lca) Father[pre]=link[i]; //对于BFS树中的父边是匹配边的点,Father向后跳 39 InBlossom[Base[i]]=true; 40 InBlossom[Base[link[i]]]=true; 41 } 42 for (i=y;Base[i]!=lca;i=pre){ 43 if (Base[pre]!=lca) Father[pre]=link[i]; //同理 44 InBlossom[Base[i]]=true; 45 InBlossom[Base[link[i]]]=true; 46 } 47 #undef pre 48 if (Base[x]!=lca) Father[x]=y; //注意不能从lca这个奇环的关键点跳回来 49 if (Base[y]!=lca) Father[y]=x; 50 for (i=1;i<=n;i++) 51 if (InBlossom[Base[i]]){ 52 Base[i]=lca; 53 if (!in_Queue[i]){ 54 Q[++tail]=i; 55 in_Queue[i]=true; //要注意如果本来连向BFS树中父结点的边是非匹配边的点,可能是没有入队的 56 } 57 } 58 } 59 60 void Change(){ 61 int x,y,z; 62 z=Finish; 63 while (z){ 64 y=Father[z]; 65 x=link[y]; 66 link[y]=z; 67 link[z]=y; 68 z=x; 69 } 70 } 71 72 void FindAugmentPath(){ 73 fill(Father,Father+n+1,0); 74 fill(in_Queue,in_Queue+n+1,false); 75 for (int i=1;i<=n;i++) Base[i]=i; 76 head=0; tail=1; 77 Q[1]=Start; 78 in_Queue[Start]=1; 79 while (head!=tail){ 80 int x=Q[++head]; 81 for (int y=1;y<=n;y++) 82 if (map[x][y] && Base[x]!=Base[y] && link[x]!=y) //无意义的边 83 if ( Start==y || link[y] && Father[link[y]] ) //精髓地用Father表示该点是否 84 BlossomContract(x,y); 85 else if (!Father[y]){ 86 Father[y]=x; 87 if (link[y]){ 88 Q[++tail]=link[y]; 89 in_Queue[link[y]]=true; 90 } 91 else{ 92 Finish=y; 93 Change(); 94 return; 95 } 96 } 97 } 98 } 99 100 void Edmonds(){ 101 memset(link,0,sizeof(link)); 102 for (Start=1;Start<=n;Start++) 103 if (link[Start]==0) 104 FindAugmentPath(); 105 } 106 107 void output(){ 108 fill(mark,mark+n+1,false); 109 int cnt=0; 110 for (int i=1;i<=n;i++) 111 if (link[i]) cnt++; 112 printf("%d\n",cnt); 113 for (int i=1;i<=n;i++) 114 if (!mark[i] && link[i]){ 115 mark[i]=true; 116 mark[link[i]]=true; 117 printf("%d %d\n",i,link[i]); 118 } 119 } 120 121 int main(){ 122 // freopen("input.txt","r",stdin); 123 CreateGraph(); 124 Edmonds(); 125 output(); 126 return 0; 127 }
然后还有一篇,链接请猛戳。。
在北京冬令营的时候,yby提到了“带花树开花”算法来解非二分图的最大匹配。
http://builtinclz.abcz8.com/art/2012/ural1099.cpp
没错,这是用来解决URAL 1099 Work Schedule那题的。时间复杂度是O(N^3)
