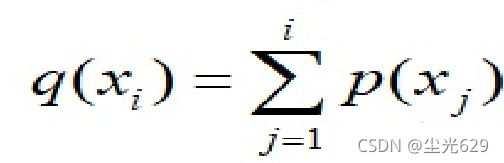仿生学的科技应用——蚁群算法简介

大家好，今天笔者与诸位分享的是智能优化算法中蚁群算法的相关知识。蚁群算法源于Marco Dorigo教授在攻读电子工程博士期间对于群体智能领域孜孜不倦的探索。顾名思义，蚁群算法借鉴了蚂蚁在寻找食物路径上的独到智慧——蚂蚁群体在复杂环境下能够依赖其生物本能找到到达食物来源的最短路径，而这项神奇本领来自于一种名为“信息素”的化学物质。蚂蚁会在其经过的路径上留下可被同类识别的信息素，当蚁群内的其他蚂蚁感知到同伴分泌的信息素后，便会沿着信息素标识的路径爬行，并分泌出更多的信息素，而越短的路径在单位时间内就会有越多的蚂蚁爬过，留下较高浓度的信息素，形成了一种正反馈调节，经过一段时间后，整个蚁群便都会沿着最短路径找到食物了。

在蚂蚁的启发下，教授开辟了解决优化问题（1）的新思路：用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体（2）的所有路径构成待优化问题的解空间，通过设置环境和信息素（为了最大限度地消除非最优解的影响，信息素在这里被设置为随时间演化而逐渐消散），将“蚂蚁路径”在正反馈的作用下集中到最优解上，从而完成优化。

介绍完蚁群算法的背景和相关原理后，我们再来看一下蚁群算法的几个步骤：

一、初始化参数

1. 蚂蚁数量m
2. 信息素常量Q
3. 最大迭代次数t
4. 信息素因子α（反映了蚂蚁运动路径中路径上积累的信息素的量在指导蚁群搜索中的相对重要程度）
5. 启发函数因子β（反映了启发式信息（3）在指导蚁群搜索中的相对重要程度，蚁群寻优过程中先验性、确定性因素作用的强度）
6. 信息素挥发因子ρ（反映了信息素的消失水平，1-ρ则反应了保持水平）

二、构建解空间

1.每只蚂蚁随机选择出发点，之后维护一个路径记忆向量来存放经过点

2.通过轮盘赌算法（4）选择下一个到达的地点

 这里做几点简要说明

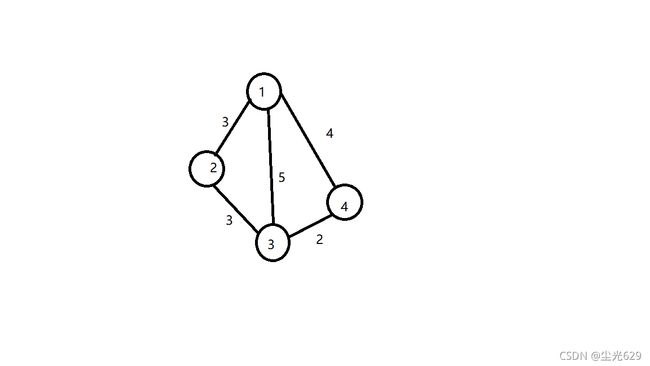
i,j为起点和终点；η表示i,j两点路径距离的倒数；τ表示经过指定时间后的信息素浓度；allowed表示尚未到达过的地点总和。下面通过一张图片来为大家进行说明。

 假设初始时所有路径上的信息素浓度均为1，信息素因子为2，启发因子为3，那么蚂蚁从4点开始，到其他地点的概率为 ps：鉴于某公式编辑器的无理取闹，这里不得已采用手写方式

 产生一个0到1之间的随机数，如果该数小于等于0.11则选择点1，大于则选择点2

三、更新信息素

相关公式(5)如下：

 这里的Lk为总路径长度

四、判断是否终止 

将从数据初始化到所有蚂蚁走完全部地点这一过程称为一次迭代，获取这次迭代中所有的路径信息并加以比较，得出最短路径，再与之前的迭代结果相比较选取更短路径，之后更新信息素，还原数据，进行下一次迭代，直至达到最大迭代次数，这时的总最短路径即为最优解。

介绍完蚁群算法的大致思路后，下面会为大家展示相应的代码。

鉴于笔者还是初学阶段(手动doge)，选取的数据量比较少，并且编写的代码还是会有不少纰漏之处，还望大家海涵。

import os
os.getcwd()
import numpy as np
import matplotlib.pyplot as plt
#导入所需的库和模块

spots=np.array([[18.47,95.10],[16.47,94.64],[20.09,94.54],[14.39,93.37],[25.23,97.24],[22.00,93.05]])
#输入6个地点坐标

def getdist1(spots):
    num=spots.shape[0]
    dist1=np.zeros((6,6))
#生成一个六阶方阵
    for i in range(num):
        for j in range(i,num):
            dist1[i][j] = dist1[j][i] = np.linalg.norm(spots[i] - spots[j])
    return dist1
#计算出六个点之间的欧几里得度量

#初始化数据，字母含义详见步骤一
m=8
Q=1
numspot=spots.shape[0]
t=150
α=1
β=3
ρ=0.2
iter=0 #迭代初始
dist1=getdist1(spots)

etatable=1.0 / (dist1 + np.diag([1e10] * numspot))
# diag(),将一维数组转化为方阵 启发函数矩阵，表示蚂蚁从城市i转移到城市j的期望程度
pheromonetable=np.ones((numspot, numspot)) # 信息素矩阵
pathtable=np.zeros((m, numspot)).astype(int) # 路径记录表
distmat=getdist1(spots) # 城市的距离矩阵
lengthaver=np.zeros(t)  # 迭代50次，存放每次迭代后，路径的平均长度
lengthbest = np.zeros(t)  # 迭代50次，存放每次迭代后，最佳路径长度
pathbest=np.zeros((t, numspot))  # 迭代50次，存放每次迭代后，最佳路径城市的坐标,一共为300

while iter 0).index(True)]
            #通过轮盘赌法选出下一个要经过的地点并求出其概率，再根据随机数所在的区间确定到达的下一个点

            pathtable[i,j]=k
            unvisited.remove(k)
            visited.add(k)
            length[i]+=dist1[visiting][k]
            visiting=k
        length[i]+=dist1[visiting][pathtable[i,0]]
    lengthaver[iter]=length.mean()
    #进行了一次完整的迭代并求出最佳路径

    if iter==0:
        lengthbest[iter]=length.min()
        pathbest[iter]=pathtable[length.argmin()].copy()
    #进行第一次迭代，选择本次最短的路径,返回索引值下标并将其记录
    else:
        if length.min()>lengthbest[iter - 1]:
            lengthbest[iter]=lengthbest[iter - 1]
            pathbest[iter]=pathbest[iter - 1].copy()
        else:
            lengthbest[iter]=length.min()
            pathbest[iter]=pathtable[length.argmin()].copy()

    # 此部分是为了更新信息素
    changepheromonetable=np.zeros((numspot,numspot))
    for i in range(m):  # 更新所有的蚂蚁
        for j in range(numspot - 1):
            changepheromonetable[pathtable[i, j]][pathtable[i, j + 1]] += Q / dist1[pathtable[i, j]][
                pathtable[i, j + 1]]
        changepheromonetable[pathtable[i, j + 1]][pathtable[i, 0]] += Q / dist1[pathtable[i, j + 1]][pathtable[i, 0]]
    pheromonetable=(1-ρ) * pheromonetable + changepheromonetable
   #不断更新信息素并进行计算

    iter+=1  # 迭代次数加1
    print("this iteration end：", iter)
    if (iter - 1) % 20 == 0:
        print("schedule:", iter - 1)
    #达到最大迭代次数，迭代完成

 这里会出现一个小问题，change~开头的语句会警告说遇到被零除的情况，不过不妨碍最终的结果。下面是笔者在编写时拓展的一些知识，为了不影响整体观感放到了最后。

1. 蚁群算法在后来的应用中主要用于处理TSP问题（即旅行商问题），是指一名推销员要拜访多个地点时，如何找到在拜访每个地点一次后再回到起点的最短路径，听起来规则虽然简单，但在地点数目增多后求解却极为复杂，是作为千禧年七大难题之一的NP完全问题的典型例题，由此可见蚁群算法的出现确实具有划时代的意义。不仅于此，蚁群算法还在通讯工程，交通运输等诸多领域取得了非凡的成就，其创始者教授本人也因此在业界名声大噪。
2. 在整个蚂蚁群体中，每一只“蚂蚁”都是平权的，这样可以在问题空间的多点同时开展独立的解搜索，不仅增强了算法的可靠性，也使得算法具备了较强的全局搜索能力。
3. 笔者发现大部分关于蚁群算法的文章都没能够详尽地解释启发式信息的具体作用，主要是一个特定名词“先验性”没有介绍清楚。为此，笔者咨询了一下心理学相关的朋友——先验性最早是由康德提出的，认为某些具有“先验”特性的东西在人的经验之前，比如一个婴幼儿要认识某种事物，会去看，去摸，得到经验后才能去判断，但是他饿了渴了会直接哇哇大哭，这是先天的能力，不需要经验。同理，如果启发式信息的重要程度过大，先验性过强，那么无论是蚂蚁还是旅行商都会表现出过分的“主观臆断”来，缺乏合理性，而过小又会无视信息素，近乎完全随机。
4. 轮盘赌选择法（roulette wheel selection）是最简单也是最常用的选择方法，在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。但实际在进行轮盘赌选择时个体的选择往往不是依据个体的选择概率，而是根据“累积概率”来进行选择。设某一部分x(i)的适应度值表示为f(xi)，该部分被选中的概率为p(xi)，累积概率为q(xi)，对应的计算公式如下：

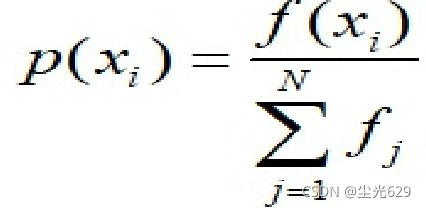
在计算完p(xi)和q(xi)之后随机生成一个取值范围在0到1之间的数组m,并从小到大排列，若q(xi)大于数组m中的元素，则xi被选中，反之则比较下一个直至选出一个个体为止。

5.蚁群算法共分为三种模型，分别为蚁周模型、蚁量模型和蚁密模型，笔者采用的是蚁周模型，在完成一次完整的路径之后，蚂蚁才会释放信息素。

在文章的最后。我要感谢csdn和b站上介绍蚁群算法等相关知识的前辈，在我编撰这篇博客时提供了很大的帮助，也欢迎看到这篇文章的每一位朋友提出自己的意见和建议，我们可以共同努力，共同进步。虽然可能有些晚了，不过还是祝大家1024程序员节快乐。