【算法合集】学习算法第二天(二分与排序篇)
✅个人主页:程序猿追
✅系列专栏:算法合集
✅目前状态:创建Java学习之路(零基础到就业实战)系列,目前更新到JAVAWEB开发
✅作者简介:大家好,我是程序猿追,全栈领域新星创作者,算法爱好者,常在作者周榜排名前30,某不知名的 ACMer
✅推荐一款刷题面试找工作三不误的网站——牛客网
✅个人名言:不积跬步无以至千里,趁年轻,使劲拼,给未来的自己一个交代!
哈喽,大家好,我是程序猿追,通过上一篇算法文的私信,有小伙伴留言说,什么时候更新呀?这不?今天它就来了。
目录
二分查找-I
题解代码
二维数组中的查找
题解代码
寻找峰值
题解代码
数组中的逆序对
题解代码
二分查找-I
描述
请实现无重复数字的升序数组的二分查找
给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1
数据范围:0≤len(nums)≤2×105 , 数组中任意值满足 ∣val∣≤109
进阶:时间复杂度 O(logn) ,空间复杂度 O(1)
示例1
输入:
[-1,0,3,4,6,10,13,14],13返回值:
6说明:
13 出现在nums中并且下标为 6示例2
输入:
[],3返回值:
-1说明:
nums为空,返回-1示例3
输入:
[-1,0,3,4,6,10,13,14],2返回值:
-1说明:
2 不存在nums中因此返回 -1
题解代码
import java.util.*;
public class Solution {
public int search (int[] nums, int target) {
int l = 0;
int r = nums.length - 1;
//从数组首尾开始,直到二者相遇 fast-template
while(l <= r){
//每次检查中点的值
int m = (l + r) / 2;
if(nums[m] == target)
return m;
//进入左的区间
if(nums[m] > target)
r = m - 1;
//进入右区间
else
l = m + 1;
}
//未找到
return -1;}
}二维数组中的查找
描述
在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
数据范围:矩阵的长宽满足 0≤n,m≤500 , 矩阵中的值满足 0≤val≤109
进阶:空间复杂度 O(1),时间复杂度 O(n+m)
示例1
输入:
7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]复制返回值:
true说明:
存在7,返回true示例2
输入:
1,[[2]]返回值:
false示例3
输入:
3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]返回值:
false说明:
不存在3,返回false
题解代码
public class Solution {
public boolean Find(int target, int [][] array) {
//优先判断特殊 fast-template
if(array.length == 0)
return false;
int n = array.length;
if(array[0].length == 0)
return false;
int m = array[0].length;
//从最左下角的元素开始往左或往上
for(int i = n - 1, j = 0; i >= 0 && j < m; ){
//元素较大,往上走
if(array[i][j] > target)
i--;
//元素较小,往右走
else if(array[i][j] < target)
j++;
else
return true;
}
return false;}
}寻找峰值
描述
给定一个长度为n的数组nums,请你找到峰值并返回其索引。数组可能包含多个峰值,在这种情况下,返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] = −∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗?
数据范围:
1≤nums.length≤2×10^5
-2^31<=nums[i]<=2^31 − 1
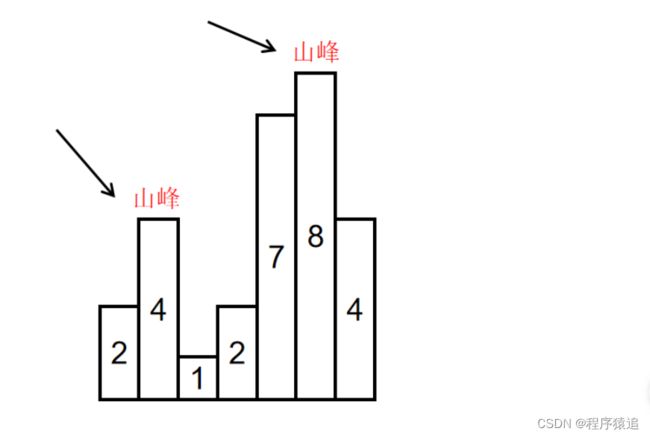
如输入[2,4,1,2,7,8,4]时,会形成两个山峰,一个是索引为1,峰值为4的山峰,另一个是索引为5,峰值为8的山峰,如下图所示:
示例1
输入:
[2,4,1,2,7,8,4]返回值:
1说明:
4和8都是峰值元素,返回4的索引1或者8的索引5都可以示例2
输入:
[1,2,3,1]返回值:
2说明:
3 是峰值元素,返回其索引 2
题解代码
import java.util.*;
public class Solution {
public int findPeakElement (int[] nums) {
int left = 0;
int right = nums.length - 1;
//二分法 fast-template
while(left < right){
int mid = (left + right) / 2;
//右边是往下,不一定有坡峰
if(nums[mid] > nums[mid + 1])
right = mid;
//右边是往上,一定能找到波峰
else
left = mid + 1;
}
//其中一个波峰
return right;}
}数组中的逆序对
描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007
数据范围: 对于 50% 的数据, size≤10^6
对于 100% 的数据, size≤105数组中所有数字的值满足 0≤val≤1000000
要求:空间复杂度 O(n),时间复杂度 O(nlogn)
输入描述:
题目保证输入的数组中没有的相同的数字
示例1
输入:
[1,2,3,4,5,6,7,0]返回值:
7示例2
输入:
[1,2,3]返回值:
0
题解代码
public class Solution {
public int mod = 1000000007;
public int mergeSort(int left, int right, int [] data, int [] temp){
// 停止划分 fast-template
if (left >= right)
return 0;
//取中间
int mid = (left + right) / 2;
//左右划分
int res = mergeSort(left, mid, data, temp) + mergeSort(mid + 1, right, data, temp);
//防止溢出
res %= mod;
int i = left, j = mid + 1;
for (int k = left; k <= right; k++)
temp[k] = data[k];
for (int k = left; k <= right; k++) {
if (i == mid + 1)
data[k] = temp[j++];
else if (j == right + 1 || temp[i] <= temp[j])
data[k] = temp[i++];
//左边比右边大,答案增加
else {
data[k] = temp[j++];
// 统计逆序对
res += mid - i + 1;
}
}
return res % mod;
}
public int InversePairs(int [] array) {
int n = array.length;
int[] res = new int[n];
return mergeSort(0, n - 1, array, res);}
}算法对程序员来说及其重要,语言和开发平台不断变化,但是万变不离其宗的是那些算法和理论,依稀记得我那个玩的很好的一个学长(在大二就拿到了 offer),他告诉我想找一个好的工作,那刷题一定是必不可少的
现在算法刷题平台还是蛮多的,给大家介绍一个我认为与大厂关联最深的平台——牛客网