数学_简述积分原理
一、积分
积分的实际上就是求面积,像正方形、长方形等都有其求面积公式,一些正多边形也可以拆分成几个三角形和矩形的和,但是对于一些不规则的面积求解就存在难度,但实际上也是可以通过分割的方法无限逼近的。
1、用无限分割的方法求面积
可以先将这部分面积用几个矩形分割,假使下面的每一段长都是 0.428

所这个时候计算出的覆盖面积是:
第一块橙色面积: S 1 = 0.428 ∗ ( 0 + 1 ∗ 0.428 ) S_1 = 0.428 * (0 + 1 * 0.428) S1=0.428∗(0+1∗0.428)
第二块橙色面积: S 2 = 0.428 ∗ ( 0 + 2 ∗ 0.428 ) S_2 = 0.428 * (0 + 2 * 0.428) S2=0.428∗(0+2∗0.428)
第三块橙色面积: S 3 = 0.428 ∗ ( 0 + 3 ∗ 0.428 ) S_3 = 0.428 * (0 + 3 * 0.428) S3=0.428∗(0+3∗0.428)
第四块橙色面积: S 4 = 0.428 ∗ ( 0 + 4 ∗ 0.428 ) S_4 = 0.428 * (0 + 4 * 0.428) S4=0.428∗(0+4∗0.428)
第五块橙色面积: S 5 = 0.428 ∗ ( 0 + 5 ∗ 0.428 ) S_5 = 0.428 * (0 + 5 * 0.428) S5=0.428∗(0+5∗0.428)
第六块橙色面积: S 6 = 0.428 ∗ ( 0 + 6 ∗ 0.428 ) S_6 = 0.428 * (0 + 6 * 0.428) S6=0.428∗(0+6∗0.428)
总面积: S = S 1 + S 2 + S 3 + S 4 + S 5 + S 6 = 0.428 ∗ ( 0 + ( 1 + 2 + 3 + 4 + 5 + 6 ) ∗ 0.428 ) = 3.846864 S = S_1 + S_2 +S_3+S_4+S_5+S_6 = 0.428 * (0 + (1+2+3+4+5+6) * 0.428)= 3.846864 S=S1+S2+S3+S4+S5+S6=0.428∗(0+(1+2+3+4+5+6)∗0.428)=3.846864
这个和我们按三角形公式计算: 3 ∗ 3 / 2 = 4.5 3 * 3 / 2 = 4.5 3∗3/2=4.5 还存在很大的差距
当我们分割成 n 个矩形, n 逼近无穷大的时候:
我们一样也是一块一块面积的计算,再汇总,只是 0.428 我们用 dx 代替,
d x = 3 − 0 n dx = \frac{3-0}{n} dx=n3−0
而6 我们用 n代替
那么总面积的公式就是:
S = d x ∗ ( 0 + ( 1 + 2 + . . . + n ) ∗ d x ) = 3 − 0 n ∗ ( 1 + n ) n 2 ∗ 3 − 0 n = 3 ∗ 3 2 ∗ n + 1 n = 4.5 S = dx * (0 + (1+2+...+n) * dx)= \frac{3-0}{n} * \frac{(1+n)n}{2}* \frac{3-0}{n} = \frac{3 * 3}{2}* \frac{n+1}{n}= 4.5 S=dx∗(0+(1+2+...+n)∗dx)=n3−0∗2(1+n)n∗n3−0=23∗3∗nn+1=4.5
用积分表示就是
∫ 0 3 x d x = 3 2 2 = 4.5 \int_0^3 {x} \,{\rm d}x = \frac{3^2}{2}=4.5 ∫03xdx=232=4.5
将3用a 替代:
∫ 0 a x d x = a 2 2 \int_0^a {x} \,{\rm d}x = \frac{a^2}{2} ∫0axdx=2a2
[注:
d:是指 ‘求差’difference,n:逼近无穷大 ( n + 1 ) / n (n + 1) / n (n+1)/n 此时逼近1, ∫ \int ∫: 只是求和sum的s拉长了 ]
2、简单推广
在将3用 b 替代, 0 用 a 替代 ,

那么总面积公式就是
S = d x ∗ ( n ∗ a + ( 1 + 2 + . . . + n ) ∗ d x ) = a ∗ ( b − a ) + b − a n ∗ ( 1 + n ) n 2 ∗ b − a n S = dx * (n*a + (1+2+...+n) * dx) = a * (b-a) + \frac{b-a}{n} * \frac{(1+n)n}{2}* \frac{b-a}{n} S=dx∗(n∗a+(1+2+...+n)∗dx)=a∗(b−a)+nb−a∗2(1+n)n∗nb−a
= a ∗ ( b − a ) + ( b − a ) 2 2 = ( b − a ) ( a + b ) 2 = a * (b-a) + \frac{(b-a)^2}{2} = \frac{(b-a)(a + b)}{2} =a∗(b−a)+2(b−a)2=2(b−a)(a+b)
用积分表示就是
∫ a b x d x = ( b − a ) ( a + b ) 2 \int_a^b {x} \,{\rm d}x =\frac{(b-a)(a + b)}{2} ∫abxdx=2(b−a)(a+b)
3、同类二次 y = x^2
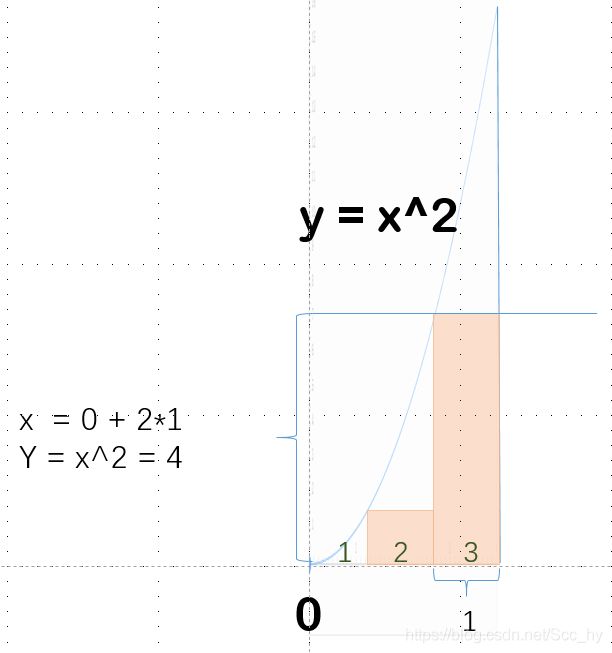
用同样的方法:
第一块橙色面积: S 1 = 1 ∗ ( 0 + ( 1 ∗ 1 ) 2 ) = 1 3 ∗ 1 2 S_1 = 1 * (0 + (1 * 1)^2) = 1^3 * 1^2 S1=1∗(0+(1∗1)2)=13∗12
第二块橙色面积: S 2 = 1 ∗ ( 0 + ( 2 ∗ 1 ) 2 ) = 1 3 ∗ 2 2 S_2 = 1 * (0 + (2 * 1)^2) = 1^3 * 2^2 S2=1∗(0+(2∗1)2)=13∗22
总面积: S = S 1 + S 2 = 1 3 ∗ ( 1 2 + 2 2 ) = 5 S = S_1 + S_2 = 1^3 * (1^2 + 2^2)= 5 S=S1+S2=13∗(12+22)=5
当我们分割成 n 个矩形, n 逼近无穷大的时候:
我们一样也是一块一块面积的计算,再汇总,只是 1 我们用 dx 代替,
d x = 3 − 0 n {\rm dx} = \frac{3-0}{n} dx=n3−0
则面积公式为:
S = ( d x ) 3 ∗ ( 1 2 + 2 2 + . . . + n 2 ) S = (dx)^3* (1^2+2^2+...+n^2) S=(dx)3∗(12+22+...+n2)
1到n的平方和 可以有推导式,建议看百度的直接拆分推导
( 1 2 + 2 2 + . . . + n 2 ) = n 3 3 + n 2 2 + n 6 (1^2+2^2+...+n^2) = \frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6} (12+22+...+n2)=3n3+2n2+6n
所以:
S = 3 3 n 3 ∗ ( n 3 3 + n 2 2 + n 6 ) = 3 3 ∗ ( 1 3 + 1 2 n + 1 6 n 2 ) = 3 3 3 S = \frac{3^3}{n^3}* (\frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6})= 3^3*(\frac{1}{3} +\frac{1}{2n} +\frac{1}{6n^2}) = \frac{3^3}{3} S=n333∗(3n3+2n2+6n)=33∗(31+2n1+6n21)=333
当长度3 用a 代替时:
S = a 3 3 S = \frac{a^3}{3} S=3a3
用积分表示就是
∫ 0 a x 2 d x = a 3 3 \int_0^a {x^2} \,{\rm d}x=\frac{a^3}{3} ∫0ax2dx=3a3
结语
由上述可知求 y = x k y = x^k y=xk 在区间 x = 0 到 x = a x = 0到 x = a x=0到x=a 的积分,必须求 ( 1 k + 2 k + . . . + n k ) (1^k+2^k+...+n^k) (1k+2k+...+nk)。
在1636年的时候,费马曾提出:
n k + 1 k + 1 < 1 k + 2 k + . . . + n k < ( n + 1 ) k k + 1 \frac{n^{k+1}}{k+1}<1^k+2^k+...+n^k<\frac{(n+1)^k}{k+1} k+1nk+1<1k+2k+...+nk<k+1(n+1)k
所以可以计算 y = x k y = x^k y=xk的积分。只要使用不等式和阿基米德夹逼定理,就可以得到:
∫ 0 a x k d x = a k + 1 k + 1 \int_0^a {x^k} \,{\rm d}x=\frac{a^{k+1}}{k+1} ∫0axkdx=k+1ak+1
