Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 论文笔记

Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 论文笔记

论文链接： https://arxiv.org/abs/1911.08287

一、 Problem Statement

Bounding Box的回归分支在目标检测中很重要。目前，$l_n$-norm loss 对获得最优的IoU metric不是很合适，IoU Loss 只有在bounding boxes 有重叠的时候起作用，而且不会提供任何移动梯度给不重叠的bounding boxes，也就是梯度消失。而GIoU Loss改善了IoU Loss的情况，但有以下缺点:

1. GIoU Loss 首先尝试增大预测bounding boxes的大小，使其与target box有重叠。通过IoU term来最大化重叠区域。因此，GIoU Loss 依赖于IoU term，需要更多的迭代去收敛，特别是对于那些水平和垂直的bounding boxes。
2. 其次，作者认为， 对于bounding box regression，一个好的loss 需要考虑三个重要的几何信息:overlap area, central point distance 和 aspect ratio。

详细的图示案例可以查看这篇博客。

所以作者提了两个问题:
4. 是否可以直接最小化normalized distance between predicted box and target box，从而加快收敛速度。
5. 当与目标框有重叠，甚至被包含的时候，怎么样使得回归更加的精准和快速。

二、 Direction

1. 针对GIoU Loss, 提出优化Iou penalty term，解决第一个问题。
2. 提出CIoU Loss, 解决第二个问题。
3. 提出DIoU NMS。

三、 Method

先来回顾以下IoU Loss 和 GIoU 的公式。
首先，IoU的定义如下:
$$IoU=\frac{|B\cap B^{gt}|}{|B\cup B^{gt}|}$$
其中，$B^{gt}=(x^{gt},y^{gt},w^{gt},h^{gt})$是ground-truth，而预测的是相对应的$B$。

基于上面式子，IoU Loss的表达式为:
$$L_{IoU}=1-\frac{|B\cap B^{gt}|}{|B\cup B^{gt}|}$$
所以，IoU Loss 只有在bounding boxes有重叠的时候奏效， 也不能提供任何的移动梯度给不重叠的情况。所以GIoU Loss 就提出来了。
$$L_{GIoU}=1-IoU+\frac{|C-B\cup B^{gt}|}{|C|}$$
这里的$C$是覆盖$B$和$B^{gt}$的框的面积。
相比于IoU Loss, 多了一个penalty term$\frac{|C-B\cup B^{gt}|}{|C|}$。由于这个penalty term，在没有重叠的情况下，预测的bounding box会向ground truth box移动。
而当两个boxes有重叠或者被包含的时候,penalty term通常很小或者为0, 收敛速度慢。
所以作者提出下面的改进方法。

1. Distance-IoU Loss

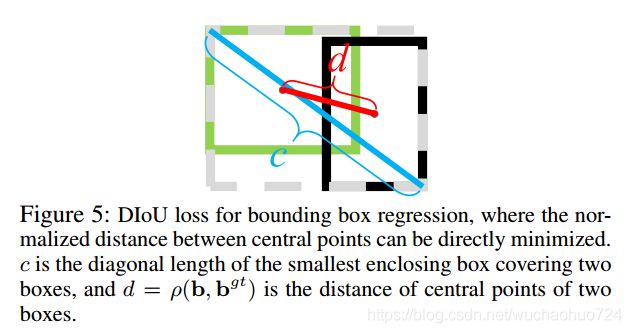
为了优化penalty term，作者提出最小化两个bounding boxes中心点的normalized distance。
$$L_{DIoU}=1-IoU+\frac{{\rho }^2(b,b^{gt})}{c^2}$$
其中，$b,b^{gt}$分别是预测框和ground-truth的中心点，$\rho$是欧几里德距离，$c$是两个框的最小包围框的对角长度。如下图所示:

因此，DIoU Loss是直接最小化两个目标框的中心点距离。

相比于IoU Loss 和 GIoU Loss,DIoU Loss也继承了以下特征:

1. DIoU Loss 对于回归问题仍然是尺度不变的。
2. 当遇到没有重叠的情况下，DIoU提供了移动方向。
3. 当两个框完美匹配的时候，三个loss 接近于0，而两个框离的很远的时候，$L_{GIoU}=L_{DIoU}\to 2$

但DIoU Loss 收敛速度快。

2. Complete IoU Loss

对于第二个问题，当与目标框有重叠，甚至被包含的时候，怎么样使得回归更加的精准和快速。 作者认为，好的 bounding box regression loss应该考虑三个重要的几何信息: overlap area, central point distance 和 aspect ratio。IoU Loss 考虑了overlap area, GIoU Loss 依赖于IoU Loss, 而DIoU Loss考虑了overlap area 和 central point distance。然而对于aspect ratio, 作者提出了下列Loss:

$$L_{CIoU}=1-IoU+\frac{{\rho }^2(b,b^{gt})}{c^2}+\alpha v$$
其中:
$$v=\frac{4}{{\pi }^2}(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h}{)}^2$$

$$\alpha =\frac{v}{(1-IoU)+v}$$

而Loss所对应的梯度为:
$$\frac{\partial v}{\partial w}=\frac{8}{{\pi }^2}(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h})\times \frac{h}{w^2+h^2}$$

$$\frac{\partial v}{\partial h}=-\frac{8}{{\pi }^2}(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h})\times \frac{w}{w^2+h^2}$$

而分母$w^2+h^2$在$h,w\in [0,1]$的情况下通常很小，很可能会产生梯度爆炸。因此为了稳定的收敛，作者简单的将$\frac{1}{w^2+h^2}$置为1。

3. DIoU NMS

原始的NMS中，重叠面积是唯一的一个考量因素，对被包含的情况会产生错误的抑制。因此作者提出了不仅仅考量重叠面积，还需要考虑两个框中心点的距离。定义如下:
$$s_i=\{\begin{array}{c}{s}_i,IoU-R_{DIoU}(M,B_i)<ϵ\\ 0,IoU-R_{DIoU}(M,B_i)\ge ϵ\end{array}$$
其中，$M$是预测的最高置信度的框，$B$是其他预测的框。$s_i$是classification score, $ϵ$是NMS阈值。 $R_{DIoU}(\bullet )$是上面DIoU Loss里面的penalty term。作者认为如果两个框中心点较远，应该是两个目标，不应该被移除。。。

四、 Conclusion

CIoU Loss 对于小目标的AP值比原始的IoU Loss表现较差而DIoU Loss是最好的。作者认为aspect ratio对小目标的regression accuracy作用不大。因为对于回归来说，中心点距离比aspect ratio更重要。而且aspect ratio可能会减弱两个框中心点normalizd distance的影响。而对于中等或者大的目标，CIoU Loss效果更好。

五、 Reference