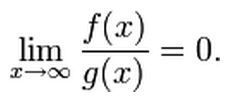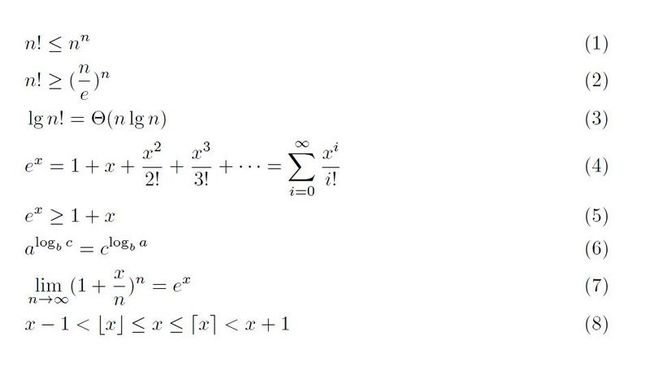漫谈算法（番外篇） 符号标记以及基本数学公式

Keywords：Big O； Little O；Big Omega；Little Omega；Theta；Mathematical Formula。

说到算法，大家最熟悉的恐怕就是这个大欧标记了，即O。什么基于比较的排序算法最好是O(nlgn)了什么的。（注，本系列文章里不区分log和lg，两个符号都是表示以二为底的对数）

更general一点，我们可以写成O(g(n))，这个东西是什么吗，其实他是一个集合，表示所以满足条件的一系列函数，这一系列函数有什么特点呢？那就是g(n)是他们的上界，更准确的说，是一个constant c， c*g(n)是他们的上界。如下图，（截自算法导论）

假设f(n)表示我们quick sort的时间，我们写作f(n) = O(nlgn)，这时候你可能要问了，刚才上面不是说O(nlgn)表示一个集合吗，这么集合里面显然都是函数，那怎么能写 函数 = 函数的集合呢？没错，其实这样写确实不好，但是我们现在已经约定俗成了，这里的等号就表示元素和集合关系的属于的符号。

现在来看一下Big O的formal的定义。

O(g(n)) = {f(n) : 存在一个正常数c，和一个 N0， 对于所有的N>N0， 0<= f(n) <= c*g(n)}

其实结合上面的图和这个定义，Big O的意思还是很明显的。他是f(n)的一个upper bound。

同理，我们可以定义 Big Omega 和 Theta。

Omega(g(n)) = {f(n): 存在一个正常数c，和一个 N0， 对于所有的N>N0， 0<= c*g(n) <= f(n) }

当然，这是我们f(n)的一个lower bound。

Theta(g(n)) = {f(n): 存在正常数c1和c2，和一个 N0， 对于所有的N>N0， c1*g(n) <= f(n) <= c2*g(n)}

下面是算法导论里面完整的图。

下面给一下Litter O 和 Litter Omega的概念。

通过上面的定义我们可以发现，在Big O，Big Omega和Theta的定义中，我们都出现了“=”，当然，类比当我们数字的比较，我们有大于等于，小于等于，同样，我们也有大于，小于。

当然对于这个等号，我们可以说是一个tight的bound，比如2n^2 = O(n^2)，这个bound就是asymptotically tight的，但是对于2n = O(n^2)来说，这个就不是tight的。所以，这时我们的Little O就孕育而生了。用算法导论里面的原话就是： We use o-notation(Litter O) to denote an upper bound that is not asymptotically tight.

下面来看Little O的formal的定义。

o(g(n)) = {f(n): 对于任意的正常数c，存在一个N0，对于所有的N>N0, 0<= f(n) < c*g(n)}

同样，我们可以定义Little Omega。

w(g(n)) = {f(n): 对于任意的正常数c，存在一个N0，对于所有的N>N0, 0<= c*g(n) <=f(n)}

============================================华丽的分割线==================================

对于这些标记，其实我们还可以从growth rate和极限的方面来考虑。

比如对于little O， it means that g(x) grows much faster than f(x), or similarly, the growth off(x) is nothing compared to that of g(x).（偷懒一下，直接从wikipedia上抄下来）

其余的大家自己也应该都可以琢磨出来。(*^__^*) 嘻嘻……

最后给几个常用且简单的数学公式，权当remind了。

========================================================================================

本作品采用知识共享署名 2.5 中国大陆许可协议进行许可。 本博客采用知识共享署名 2.5 中国大陆许可协议进行许可。本博客版权归作者所有，欢迎转载，但未经作者同意不得随机删除文章任何内容，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。如您有任何疑问或者授权方面的协商，请给我留言。