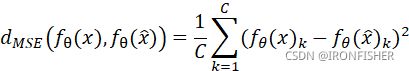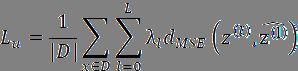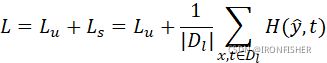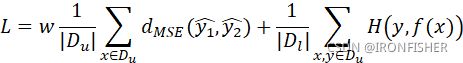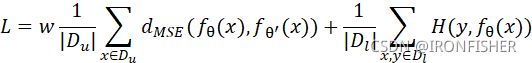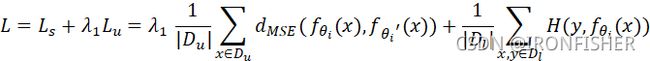半监督学习笔记（二）：一致性正则化

Introduction

原文链接

https://arxiv.org/abs/2006.05278v2https://arxiv.org/abs/2006.05278v2

昨天的更新讲了一下半监督学习的Overview部分，简要的复习一下：

半监督学习的概念：大部分数据没有标注，少部分数据有标注，然后半监督学习要对这些数据执行良好的分类任务。

半监督学习的方法：一致性正则化，代理变量，生成模型，基于图的方法。

半监督学习的基本假设：平滑性假设、聚类假设、流形假设

半监督学习的相关问题：主动学习、迁移学习和域适应、弱监督学习、从噪声中学习。

半监督学习算法的衡量：共享信息、高质量监督基线、与迁移学习比较、考虑类分布的不匹配、改变标记数据的数量、用较小的验证集。

今天学习第二章：一致性正则化(Consitency Regularization)

首先要说明，什么是正则化？

首先，我们要肯定一个事实：神经网络存在着欠拟合和过拟合的事实。欠拟合，就是模型不能良好的拟合函数的特征，而过拟合，就是函数对模型拟合的太好了。导致给予了过多的关注在每个数据的细节方面，而忽略了数据的整体特征。而正则化，就是为了解决这个问题的。那么一致性是什么意思呢？让我们回想一下聚类假设：假设这两个点在同一类（或者距离十分的接近），他们的输出也会接近。一致性就是为了使得训练的函数fθ有如下性质：任意给定两个输入和 ，假设他们的欧式距离足够近，那么他们的输出和能够相近。所以组合起来，一致性正则化，就是为了让函数能有这样的性质。

那么，用于度量这个一致性正则化效果的指标有哪些呢？对于训练神经网络而言，在损失项上加一个L2-norm即可，但这是对于模型中的参数值的。对于半监督学习而言，也有L2-norm，但这求的是两个输入,以及他们的输出和之间的距离：

除了MSE，还有其他的距离，比如Kullback-Leiber divergence(KL)和JenSen-Shannon divergence。

那接下来，我们就来介绍一些一致性正则化模型.

一致性正则化模型

2.1 Ladder Networks.

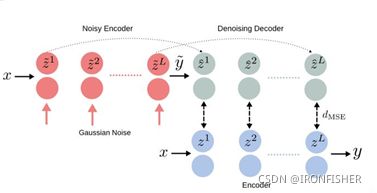
这是一个最简单的一致性正则化模型，核心思路很简单：如果需要网络对噪声不敏感，那不如训练的时候就直接加上噪声！然后把噪声项放到损失函数里面去。核心架构如下：

原理也很简单，假设神经网络是一个编码层，那么Ladder Networks就加入了解码层，编码层分成两部分，一部分是干净的编码层，x输入后直接输出y，另一部分是x输入后，在批次归一化时中加入噪声，然后输出被污染后的输出，然后再进入解码层，还原出在编码层中的每一个输出，能还原的越好，就说明网络编码的越好，损失也就越低。这就是半监督学习的损失函数计算，最后公式如下：

 

其中，第一个求和与平均是对该迷你批次中的每一个x代到后面表达式的计算值进行求平均，第二个求和是对每一个输入，对在decoder和无污染模型的每一层输出计算平方损失函数，再乘以一个系数，这就对不同层数的重要性进行了区分。

那么这只是半监督学习-一致性正则化中的损失函数计算，整体的损失当然还要有给定的，因此最后的计算结果为：

这种编码结构可以在卷积神经网络中很好的应用，通常在卷积神经网络的最后一层是全连接层，正好可以通过这种方式来代替，而前面的特征提取部分则不用改动。

然而，这种方法对计算量要求十分的大，每一次迭代中，大概需要三倍的计算量。那么，接下来让我们看看2.0版本是怎么样的吧！

2.2 Pi-Model

在神经网络的学习中可以知道，其实在神经网络中加入dropout层可以很好的防止过拟合，因为这能减少各个神经元之间的相互依赖性。加入了dropout层之后，在每一次minibatch迭代中都随机的Unable一些神经元，在多次迭代的训练中还能起到集成学习的作用，这样能大大的提高网络预测的准确性。因此dropout也是一个正则化的好方法，那么对于无监督学习而言，同时，对数据进行增强（对于图像数据而言，可以有仿射变换或者裁剪）也是一个好方法。那么pi-model就是这两个方法的一个应用。

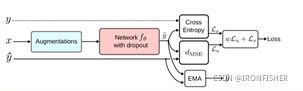
算法流程如下：

首先还是一个输入及其标签，经过增强后产生两个输出和，经过一个带有dropout层的神经网络之后输出两个值y1和y2,当然，这两个值在形式上是等价的，因此，只需要取一个和标签y1求交叉熵（对于分类问题而言），然后对这两个值本身取求MSE，再乘上一个权重，最后相加，就成了最终的输出。公式如下：

 其中，w是一个权重函数。在训练初期时，因为模型很不稳定，因此无监督学习的误差不是很有用，可能会造成随机预测的结果。所以在初期会很小，大概经过20%的次数迭代之后，会到达一个最大值λ。

但这种模型仍然存在着问题，主要为：网络每次只考虑了单个迷你批次的输入，而没有考虑所有数据的信息。从采样的角度来看，采样得到的数据集是对真实分布的一种采样，从一般情况来看，采样频率至少要大于等于奈奎斯特率才能还原真实分布，但多数情况我们是没有办法达成的，而minibatch更是对采样得到的数据集的一种估计，他与真实的数据分布的差距自然会更大。而在minibatch的训练中，只有多个minibatch的共同训练，相互影响，才能使得对真实数据的分布估计的更加准确。因此，单单考虑一个minibatch是不够的，所以说，对于无监督损失的衡量，就诞生了时间集成方法。

2.3 时间集成（Temporal Ensembling）

关于时间集成方法，它对每一个无监督的输出，它都计算了其指数的加权平均,计算公式如下：

从直观上看，每一个的更新都是对之前的数据的值与当前值的加权平均，这样模型就很好的记住了之前的输出就能相互学习。

做个比喻，当然就是温故而知新了，当我们在复习备考时，一次minibatch就相当于做一套套题，梯度下降就相当于订正这张试卷，但是对于每一次新的minibatch，我们就不再复习之前的错误，因此时间久了我们就会忘掉前面做的卷子，这样效率就很差。指数平滑法就是利用了这种“复习”的思路，当前的卷子要订正，之前的错题也要整理。

算法流程图如下：

α就是一个动量项，α越小，之前的信息对网络的影响就越小，当α=0时，时间集成模型退化为pi模型。一个输入经过增强和有dropout层的神经网络，分别与之前的输出，标签计算平方损失函数和交叉熵，最后带上权值相加成为最后的loss。 

 当然，光这样是不够的。在这里我们很容易能关注到一个问题：在初始化的时候，=0，但是此时输出不为0，在初始几次迭代中，这样计算出来的MSE值会很大，同时因为网络没有训练好，所以说还是按照老规矩，公式更新如下：

T是训练迭代次数。这是什么意思呢？在开始训练的时候，时间集成模型会退化至pi-model。这样的训练方法也有两个好处：一个是只需要一次前向传播，就可以计算出最后的结果，这大大的减少了计算时间（在深层网络中，一次前向传播的时间开销是很大的），另外该通过指数加权平均法也很好的防止了模型的不一致性。但是这样也有缺点：这需要有大量的内存来保存所有训练实力的预测集，对于大数据集的情况来看，这样对训练的要求也是很高的。

Pi-model和时间集成模型都采取了集成学习的思想。然后也采取了teacher-student的训练思路，不过是自己当老师，自己当学生，也就是有监察机制（想象这是一个政府部门的话，就是加了纪委），能比较好的解决抽样与分布的问题。但是，这也造成了一些问题：由于加权的原因，假设α值设的很大，那么新的新学到的信息需要完全被模型考虑到，需要经过很长的时间。而α值设的很小，之前的信息又不会被考虑的那么充分，那么导致一次的误差只会在一次minibatch训练中得到更新。

而且这个模型也有问题，因为在每一次训练中，都是“自己教自己”，用政府来类比，内部的纪委是不够的，它还要接受群众来监督。而自己教自己的结果是什么呢？假设在某一次训练中，无监督的损失的权重超过了有监督的损失，那模型就会被阻止学习新的信息，比如预测相同的目标。转而只把精力投入在无监督损失的优化当中。因此，对于模型预测的目标还是需要进行优化，方法如下：

1. 仔细的选择噪声，而不是仅仅选择加性或乘性噪声。
2. 仔细的选择导师模型，这个导师模型要对生成的学习目标负责，而不是简单的用学生模型来“自己教自己”。

为了实现这些目标，Mean teachers就出现了。

2.4 Mean teachers

 Mean teachers，顾名思义，就是“平均值教师”。这是什么意思呢？就是对模型也做一次指数加权平均！通过EMA之后生成了，这样模型就会更加稳定，然后再对加入一个噪声。因为是通过加权平均得到的，因此跟相比会更加稳定和可靠，也是对于真实的映射fθtrue的更好的估计。所以，对加入噪声，所得到的输出也会更加稳定和可靠。也能更好的与的输出求平方损失，最后进行反向传播。

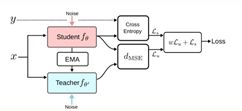
上图就是Mean teachers算法的流程，从整体设计思路上来看，同样是一个集成学习的进阶版。模型参数θ的更新公式如下：

上式就是一个简单的指数加权的公式，模型的损失函数计算如下

当然上面的模型还是有一些问题。随着训练次数的不断增加，每一次参数的更新也在不断的减小，可能也就前20%参数变化的最大，后面可能基本没怎么变。再利用指数加权平均的方法，那么teacher-model最终会收敛至student-model。所以说，如何解决这个问题呢？

2.5 Dual Students

为解决以上问题，双学生模型应运而生！所谓双学生模型，就是两个网络初始化的策略不同，参数不同。就相当于大家的目标都是高考的话，之前的模型都是一个学生在自嗨，现在就变成了两个学生在相互竞争，这两个学生的初始状态（比如天赋、智商）等，就是由不同的初始化策略得到的。在训练的过程中，每个学生都把自己对题目x做出的答案y交给对方。判断哪个学生更加好的策略，我们应采取如下方法：

是权值，第一个是一致性正则化的损失，两个模型对迷你批次中每一个输入求输出，再求这两个输出之间的平方损失函数，再对每一个输入的平方损失函数求平均。第二个表达式就是对于预测标签的损失。

1.给学生正常的输入x和带扰动的输入，模型应该有相同的输出：

2.这两个输出都是十分的可靠的，他们都应该远离决策边界。对于分类问题来说，可以通过观察最后softmax后的输出来比较。

对于两个模型，他们的损失函数计算公式如下：

当然，去考试的时候两个学生都应该答对。正确的卷子千篇一律，错误的卷子各不相同。因此，在算法中，我们也希望模型的输出都相接近。在每一次迭代中，我们只选择更加不稳定的模型去更新。

——————————————————————————————————————————

码不动了，后面还有五个模型没有更新，之后再慢慢看吧。同时对前面的每一个模型也没有理解透彻，还需要反复推敲再回来更新。