卷积神经网络初步(零):从原始汤到细胞
前言
生物界将生命的起源看作是一场必然的巧合。
曾几何时,地表尚处一片汪洋之中。剧烈的板壳运动可谓此起彼伏遥相应和。当是时,无论从何等的角度,那片汪洋也无法被称作生命的摇篮。灼热的水体不时沸腾,火山中喷发出的硫质使海水变得浑浊,连沸腾的水蒸气也染上了火山灰的颜色。然而就在这一片地狱景象中,生命的最初形式正悄然诞生——依附于海底火山口的多孔岩柱内的细小孔隙,地球上的第一批有机物就这样在不知不觉中形成。
从无到有往往是最难的一步。在此之后,出于某种冥冥之中的本能,岁月变迁中,有机物们形成自发地形成了简单的细胞器。在数万年的时间里,随着地壳渐渐趋于平稳,海底的火山一座座逐渐熄灭坍塌,活下来的本能促使生命进化成了某种更加强韧的形式——细胞。生命们为了追逐营养自发聚集到了一起形成了更加复杂的整体,在之后粗糙的整体又渐渐分化,为了不同的功能把自己特化,甚至交出自己的生命只为整体的更好生存。最终诞生了我们目前所能见到的一切生命。
将一项技术与整个生命相比较或许有些不知天高地远。但其实,深度学习领域的进化又何尝不是一次必然的巧合,一场为了一个简单目的不停进化的旅程?
0_一碗原始汤——感知机模型
20世纪20年代,曾有人提出一种名为原始汤的理论。认为在45亿年前,在地球的海洋中就产生了存在有机分子的“原始汤”,这些有机分子是闪电等能源对原始大气中的甲烷、氨和氢等的化学作用而形成的。虽然后人在一次次的实验中逐渐对这个理论提出了质疑,但仍未可否认的是,这个理论为后世的生命起源理论提供了宝贵的前置知识。
感知机是20世纪50年代末美国科学家罗森布拉特发现的一种网络模型。该模型由两层神经元所组成。如图所示。假设我们需要学习的是一组形式为y = f(wx+b)的对应关系,有输入向量(x1,x2,x3),y为最终的输出信号。我们为w赋初值为(w1、w2、w3),将向量X的加权和输入一层感知机,感知机中y‘=wx+b 若不等于y,则回过头来更新w和b。
这个时候让我们稍稍回顾我们文章的题目:卷积神经网络。因为在这里,一个卷积神经网络的里重要的组成已经呼之欲出:
-
激活函数(Activation Function)
-
对卷积神经网络的有所了解的同学,一定对这个名词不陌生,再进一步,或许也了解过卷积神经网络中应用最广泛的ReLU激活函数。

-
但首先,所谓激活函数,激活的是什么呢?
-
让我们再次回到感知机模型上。我们向感知机中输入了y = wx+b,那我们如何能够知道这个值是否可以作为输出值呢?下式是一个简单的判断函数,激活函数的工作与之相似。当我们向神经元中输入y = wx+b时,激活函数会判断这个值是否符合神经元的输出条件,若符合则输出,若不符则返回继续训练,更新w和b的值。
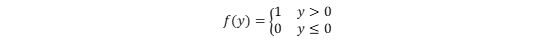
*所以,激活函数所激活的可以简单理解为当前神经元的输出功能,也可以是下一层神经元或者输出层的输入功能。
有了激活函数的知识,让我们再去看感知机的训练过程。不符合时我们要更新w和b的值,那要如何更新呢?感知机有自己的更新方法。我们以w1为例:
w1(新) = w1(旧)-Lr(w1x1+b-y)x1,其中Lr是学习率。
在机器学习、统计学或者概率学等学科中,将单个预测值与真值之间的差称为损失值,也即误差值,上文中为(w1x1+b-y)。对于感知机这种简单模型来说,由于其模型简单,承担的任务简单,损失值这种简单的插值能够承担其要求。但跳出感知机来看,对于复杂模型而言,损失值实在是个过于粗糙的衡量方式。因此我们往往会引入损失函数来达成目的。
-
损失函数(Loss Function)
- 一言以弊之,损失函数是对误差(损失值)进行操作以量化误差(损失值)的负面结果。对于现代网络而言,损失函数往往为非线性。
- 由于本文是这个系列的开篇,主要是以讲述深度学习发展历程为主线,梳理在卷积神经网络之前出现的网络结构以及对现代网络模型的重要组件的出现进行简单讲解。由上文,损失函数并非深度学习领域所独创,其应用场景也远非深度学习所能覆盖。故我们不对损失函数的原理进行详细讲解,只以一句话捎带过。后续将会对损失函数做出专门的讲解文章,请耐心等待,我会尽快更新的。
通过以上的讲解,我们应该对感知机模型有了一个大概的认识。那么我们留一个作业,给定一个由n个点组成的二维点集,给定其对应的i个类别以及y=ax+b的关联形式,是否可以对另一组点进行分类呢?
1_岩洞中的是整个人类——BP神经网络
各位有思考上一章节最后的问题吗?如果你稍加思考,答案或许不难得出:
可以。
感知机是一个线性模型。这意味着单个感知机神经元所能输出的值只有两个。正式一点说,感知机学习的目标是求得一个能够将训练数据集正实例点和负实例点完全正确分开的分离超平面。如果是非线性可分的数据,则最后无法获得超平面。

如果要进行如问题所述的多类别分类(通常简称为多分类),则需要通过对多个感知机的输出进行综合,即在二维中建立多个超平面进行划分。
有一些复杂,但是还是不难理解是吗?那我们改一下问法:
给定一个由n个点组成的二维点集,给定其对应的i个类别以及y=ax^2+b的关联形式,是否可以对另一组点进行分类呢?
答案还是可以吗?
1969年,“AI之父”马文·明斯基和LOGO语言的创始人西蒙·派珀特共同编写了一本书籍《感知机》。在这本书中,他们证明了单层感知机模型无法解决线性不可分(异或)问题。
感知机的时代在不知不觉间悄然落幕。
正如我们复杂却健全的身体里已然找不到生命最原始的模样,对感知机来说,虽然其在各种领域早可以算作不复存在(要是有谁现在还在用感知机做科研或者工作,记得叫我去观摩),但现代神经网络的鼻祖正悄然诞生。1986年,深度学习之父杰弗里·辛顿提出了反向传播算法(Back Propagation,BP),正式将神经网络由简单引向了复杂。
-
反向传播
-
若我们把从左到右当作前向,则数值在类似输入层、神经元、输出层这样的方向的传播就被称作前向传播。
-
有前向传播,自然便会有反向传播。下面我们再把感知机的幕布拉开一角,把反向传播过程与感知机的训练组合起来,来看反向传播的基本工作原理。
-
我们说以初始的权值(w1,w2,w3)和b形成的y’,很可能并不能满足神经元的激活函数要求,无法输出。我们只能反过头来更新w和b。首先我们要计算误差:1/2(y’-y)^2。这里的y指的是真值。对于(x1,x2,x3)中的每一个值,都要计算误差,并求和得到总误差E。
-
下一步我们计算每一个权值对总误差的影响因子k,并以此得出对每一个权值的修正值。
影响因子以偏导形式计算。
**E1 = 1/2[(w1x1+b)-y]^2 -
E2 = 1/2[(w2x2+b)-y]^2
-
E3 = 1/2[(w3x3+b)-y]^2
-
E = E1+E2+E3**
-
以k1为例,k1 = (±)dE/dw1(正误差为正,负误差为负),则更新后的w1为w1(±)Lr*k1(正误差为负,负误差为正),Lr即学习率。
-
以上就是反向传播在每一个神经元中的基本过程。
是不是还是不明白为什么BP算法的出现对于多层神经网络的重要性?我们将单层感知机罗列,变成多层感知机看看。

我们复习一下前面的知识,感知机模型本质是一个线性的二分模型。因此对于多层的感知机来说,由于层与层之间都是全连接的,不论叠加多少层,感知机的输出仍然是线性的。这意味着即使叠加多层也无法用感知机来解决非线性任务。 前面我们说过,感知机在计算y = ax+b后,还要经过一步激活函数才能向前传递,这是不是说明,如果我们将激活函数替换成一个非线性函数,感知机就能够解决非线性问题呢?
历史给出的答案是:Yes, use Sigmoid.
-
Sigmoid
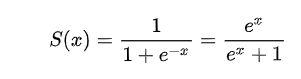
- 我们先来看看非线性激活函数的基本要求:1)函数形式要简单,节省计算时间; 2)函数要能将输入处理到(0,1)的区间上。
- 上式便是Sigmoid激活函数,神经网络历史上第一个广泛应用的非线性激活函数。它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1。并且其导数求解容易,因为其导函数可以用自身来表示。
这个时候我们使用感知机的权重更新方法来更新我们新的网络,就会发现一个巨大的问题:时间复杂度。若激活函数为3次函数,时间复杂度甚至能够到达O(n^3)。这对于模型的训练来说无疑是个灾难。
相比之下,反向传播算法在时间复杂度上则只有O(n)。
-
梯度下降算法
-
上文中我们声称损失值的精度不够进行权重更新,因此要使用损失函数来替代。
-
若使用损失值来衡量模型训练程度,那么损失值降至0或许是直觉中最佳的方式,但我们也知道物极必反,对于某一些数据的完全表征往往意味着对其他数据表征较差。其原因亦不难理解,我们所选择的样本无法完全代表数据的情况,能完全代表数据情况的通常只有全部数据。
-
如果把损失值看作一个函数在某点的值,那寻找到这个函数的极小值点就意味着寻找到了训练的终点(仅单一极点情况)。但我们显然无法根据单一值判断损失值本属于什么函数,因此根据经验选取一些可能的函数式就成了极为可行的措施。
-
是不是觉得耳熟?这些函数式就是损失函数。
-
到这里,权重更新的过程就转变成了寻找或接近损失函数极值的过程。极值的寻找依赖一阶偏导数的求取,进一步说明是依赖梯度。
-
梯度表征的是,在变量空间的某一点处,函数沿梯度方向具有最大的变化率。那么训练时,我们自然是沿着负梯度方向去减小函数值,以此达到我们的优化目标。这种使用梯度的极值寻找方法就是所谓的梯度下降算法。
到这里,现代的神经网络构架已初具轮廓,只欠最后一步。
2_再见,岩洞——深度学习
历史的钟摆巡回往复,指针一次次刻下或清晰或模糊的节点,我们将迎来完全意义上的现代神经网络。
在开始之前,我想问大家一个问题,我们前面讲述的种种网络构成中,哪一个是对网络的发展推动最大的呢?又或者,哪一种总是在关键节点出现,引领历史迈出大大的一步呢?
答案暂且按下不表,我们先回到2006年,看看在当年困扰着反向传播算法的两个问题:
-
梯度消失和梯度爆炸
- 二者可以统称为梯度不稳定问题。梯度消失指的是,当网络层数足够深的时候,靠近输入的层比靠近输出的层梯度变化更小,权值更新更慢,极端情况下前层的梯度会陷入停滞;梯度爆炸则相反,靠近输入的层比靠近输出的层梯度变化更大,权值更新更快。
造成这个问题的元凶和问题的答案相同。大家猜到了吗?
是Sigmoid激活函数。
我们先来看看函数以及对应导数的图像。

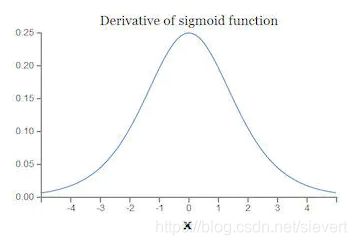
可以看到,虽然Sigmoid能够将足够大和足够小的值抹平为0和1,但由于其导数的值域为(0,0.25),当层数增多时,不断相乘的小数最终使得函数的值无限趋近于0,导致了梯度消失。同样的,当权值过大时,函数的输出大于1,梯度爆炸最终也会发生。
要理解清楚这个问题,我们还是得举个例子。让我们简单回顾一下在深度学习出现之前,要实现非线性问题,一个神经网络需要具备哪些构成呢?
我们尝试一个典型的多分类问题。
假设我们的初始样本是一组n个形式为(x1,x2,y)的三维点集,其中y值共有k个。我们需要学习x与y间的对应关系,并对另一组x值的y进行预测。
-
- 建立输入层。将(x1,x2,y)的点集传入。
-
- 建立感知机神经元。设y = w1x1+w2x2+b。赋初值进行训练。
-
- 激活函数(激活层)。使用非线性激活函数已将线性的感知机输出处理为非线性。
-
- 有k个y值,则建立k个感知机神经元+激活函数(即隐藏层)的组合。
-
- 对隐藏层中的每个神经元都进行训练。按照反向传播方法进行权重更新。
-
- 建立输出层。将激活层的输出与样本的y值作比较,距离最近的值作为最终的输出值。
-
- 若无法得到较为可信的结果,尝试加深网络,加入更多的隐藏层。而后重复5-6步。
对于区区3、5层的网络来说,或许上述过程不会出现什么问题,但当问题需要我们构建几十上百层网络才能解决的时候,寻找合适的初始权重就成了一个极大的难题。甚至对于某些问题来说,寻找这样一个数值是不可能的完成的任务。
神经网络难道真的逃不出这个窠臼了吗?
时间来到2006年,杰弗里·辛顿在Reducing the dimensionality of data with neural networks一文中提出了他的解决方案。即:在使用感知机神经元进行训练之前,先将输入层放入一个深度自解码网络中寻找权重的初值,而后再将权重作为感知机神经元中权重的初值。文章以二值图片为输入,将多层限制玻尔兹曼机作为深度自解码网络,取得了不错的效果。
这套解决方案似乎解决了梯度不稳定的难题。但其实仔细思考便会发现,是否对于所有输入类型都能寻找到像多层限制玻尔兹曼机这样合适的深度自解码网络?况且,方法也并没有触及核心。导致梯度不稳定的并不是不合理的初始权值,不如说也正是因为激活函数的不合理才导致我们如此难寻找到一个合适的初始权值。最关键的方法,还是要对激活函数进行更新。
但神经网络终究还是喘了一口大气,活了过来。还是在上文中,杰弗里·辛顿首次提出将种种网络归纳到一个名称下,这便是日后受到无数人追捧,明明属于机器学习大类却反而渐渐与之并驾齐驱的一门科学————
深度学习。一门从细微毫末中摸索而出,并将在未来的某天生长为参天巨木的科学,从那一刻,正式诞生了