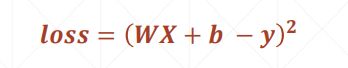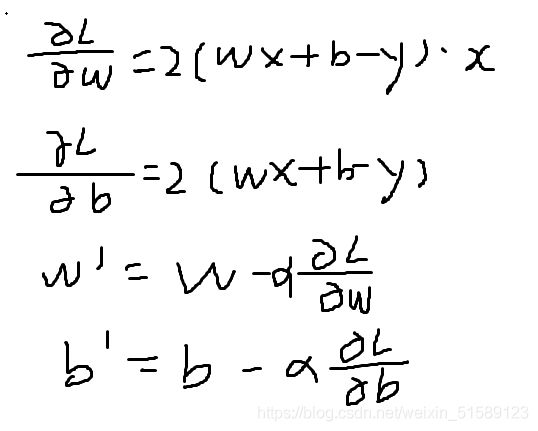pytorch的功能+线性回归、逻辑回归和分类的区别+回归问题实战+非线性转换+手写数字识别案例
目录
一、pytorch能做什么?
2、自动求导
3、常用网络层
二、线性回归、逻辑回归和分类的区别
三、回归问题实战
1、定义损失函数compute_error
2、定义梯度下降法step_gradient
3、迭代优化gradient_descent
4、输入数据
代码段
四、激活函数,非线性转换
五、手写数字识别案例
一、pytorch能做什么?
这里本来要比较在Cpu和cuda上跑代码的区别,但是我们没钱没显卡,带不动cuda
import torch
import time
import torchvision
print(torchvision.__version__)
print(torch.__version__)
#1.8.1+cpu
a = torch.randn(10000, 1000)
#1万行,1千列的矩阵
b = torch.randn(1000, 2000)
#1千行2千列的矩阵
#print(torch.cuda.is_available())
t0 = time.time()
c = torch.matmul(a, b)
#矩阵 a 和 b进行运算
t1 = time.time()
print(t1 - t0)
#0.18988704681396484
2、自动求导
#自动求导功能
import torch
from torch import autograd
x = torch.tensor(1.)
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)
y = a**2 * x + b * x + c
#函数为y
print("before:", a.grad, b.grad, c.grad)
#运行之前 y对a,b,c的偏导
grads = autograd.grad(y, [a, b, c])
#求y对a,b,c的偏导
print("after:", grads[0], grads[1], grads[2])
'''
before: None None None
求导之前是没有值得
after: tensor(2.) tensor(1.) tensor(1.)
y对a,b,c求偏导之后的值分别为2,1,1
'''
3、常用网络层
二、线性回归、逻辑回归和分类的区别
梯度下降法在深度学习部分已经学习过了,不多做介绍了,嘿嘿
linear Regression——我们要估计连续函数的值;
logistic Regression——在上述linear regression的基础上增加了一个激活函数,把y的空间压缩到0-1的范围,0-1可以表示一个概率
classification——所有的可能性概率之和为1
三、回归问题实战
1、定义损失函数compute_error
2、定义梯度下降法step_gradient
3、迭代优化gradient_descent
输入初始w和初始b
4、输入数据
代码段
import numpy as np
def compute_error(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (w * x + b)) ** 2
return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2/N) * (y - (w_current * x) +b_current)
#损失值对b进行求偏导之后,在对b_current进行更新,倒数的累加跟除以n抵消
w_gradient += -(2/N) * x * (y - (w_current * x) +b_current)
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
def gradient_descent(points, starting_b, starting_w, learning_rate, num_iteration):
b = starting_b
w = starting_w
for i in range(num_iteration):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def run():
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0
initial_w = 0
num_iteration = 1000
print("gradient_desent at b = {0}, w= {1}, error={2}".format(initial_b, initial_w, compute_error(initial_b, initial_w, points)))
print("Running···")
[b, w] = gradient_descent(points, initial_b, initial_w, learning_rate, num_iteration)
print("After{0}iterations b={1}, w={2}, error={3}".format(num_iteration, b, w, compute_error(b, w, points) ))
if __name__ == '__main__':
run()
'''
gradient_desent at b = 0, w= 0, error=5565.107834483211
Running···
After1000iterations b=0.08989889221785105, w=1.4812542263671995, error=112.64530033200117
'''
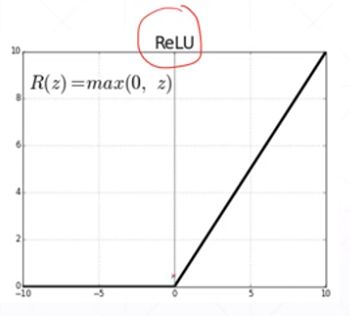
四、激活函数,非线性转换
考虑Non-linear Factor
加入激活函数之后pred既有线性表达能力,还有非线性的表达能力
五、手写数字识别案例
需要四步:
(1)load data
(2)build model
(3)train
(4)test
import torch
from torch import nn
from torch.nn import functional as F
from torch import optim
import torchvision
from matplotlib import pyplot as plt
from utils import plot_image, plot_curve, one_hot
batch_size = 512
# step1. load dataset
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('mnist_data', train=True, download=True, #如果我们没有这个文件,自动从网络上下载
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(), #将数据转换为tensor格式
torchvision.transforms.Normalize( #正则化,是像素在0-1之间均匀分布
(0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=False)
# 一次加载多少次图片
x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), x.max())
#torch.Size([512, 1, 28, 28]) torch.Size([512]) tensor(-0.4242) tensor(2.8215)
#一共拿到了512张图片,1个通道,28行,28列,label一共有512个
plot_image(x, y, "image sample")
#创建网络
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
#要建三层*
self.fc1 = nn.Linear(28*28, 256)
self.fc2 = nn.Linear(256, 64)
self.fc3 = nn.Linear(64, 10)
def forward(self, x):
#x:[b,1,28,28]
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
optimzer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []
for epoch in range(3):
for batch_idx, (x, y) in enumerate(train_loader):
#x:[b,1,28,28], y:[512]
#[b, feature]
x = x.view(x.size(0), 28*28)
# => [b, 10]
out = net(x)
y_onehot = one_hot(y)
#loss = mse(out, y_onehot)
loss = F.mse_loss(out, y_onehot)
optimzer.zero_grad()
loss.backward()
optimzer.step()
train_loss.append(loss.item())
if batch_idx % 10 == 0:
print(epoch, batch_idx, loss.item())
plot_curve(train_loss)
#we got optimal [w1, b1, w2, b2, w3, b3]
total_correct = 0
for x, y in test_loader:
x = x.view(x.size(0), 28*28)
out = net(x)
# out: [b, 10] => pred: [b]
pred = out.argmax(dim=1)
correct = pred.eq(y).sum().float().item()
total_correct += correct
total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)
x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')
#test acc: 0.888