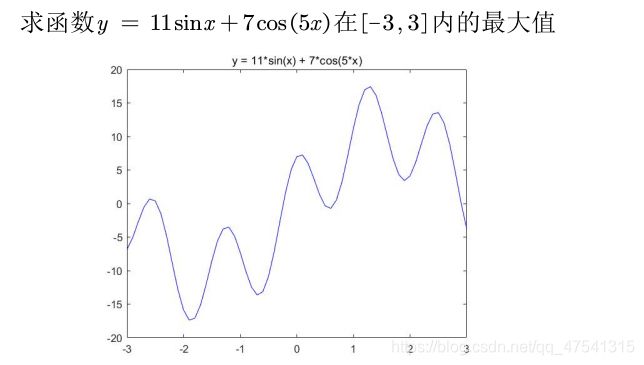
matlab-day3

参考清风数学建模资料粒子群章节

今日学习算法：

粒子群算法

定义：它的核心思想是利用群体中的个体对信息的共享使

整个群体的运动在问题求解空间中产生从无序到有序

的演化过程，从而获得问题的可行解。

自己理解的流程图：

 

理解概念：

Ø粒子：优化问题的候选解

Ø位置：候选解所在的位置

Ø速度：候选解移动的速度

Ø适应度：评价粒子优劣的值，一般设置为目标函数值

Ø个体最佳位置：单个粒子迄今为止找到的最佳位置

Ø群体最佳位置：所有粒子迄今为止找到的最佳位置

核心公式：

  

 

参数说明：

c1 ： 个体学习因子， 也称为个体加速因子。

c2 ：社会学习因子， 也称为社会加速因子 。

（在最初提出粒子群算法的论文中指出，个体学习因子和社会学习因子取2比较合适。）

r1,r2：[0,1]上随机数。

w ：称为惯性权重， 也称为惯性系数。

（查略文献得到的结论：惯性权重取0.9‐1.2是比较合适的，一般取0.9就行。）

例子：

 

具体符号说明：

 

设置粒子群算法的参数

n = 10; % 粒子数量

narvs = 1; % 变量个数(函数中有几个自变量)

c1 = 2; % 每个粒子的个体学习因子

c2 = 2; % 每个粒子的社会学习因子

w = 0.9; % 惯性权重

K = 50; % 迭代的次数

vmax = 1.2; % 粒子的最大速度

x_lb = -3; % x的下界

x_ub = 3; % x的上界

注释！！！：

(1) 增加粒子数量会增加我们找到更好结果的可

能性，但会增加运算的时间。

(2) c1,c2,w这三个量有很多改进空间，未来我再

来专门讲怎么去调整。

(3) 迭代的次数K越大越好吗？不一定哦，如果现

在已经找到最优解了，再增加迭代次数是没

有意义的。

(4) 这里出现了粒子的最大速度，是为了保证下

一步的位置离当前位置别太远，一般取自变

量可行域的10%至20%(不同文献看法不同)。

(5) X的下界和上界是保证粒子不会飞出定义域

初始化粒子的位置和速度

x = zeros(n,narvs);

for i = 1: narvs

% 随机初始化粒子所在的位置在定义域内

x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);

end

% 随机初始化粒子的速度，设置为[-vmax,vmax]

v = -vmax + 2*vmax .* rand(n,narvs);

计算适应度

fit = zeros(n,1); % 初始化这n个粒子的适应度全为0

for i = 1:n % 循环整个粒子群，计算每一个粒子的适应度

fit(i) = Obj_fun1(x(i,:)); % 调用Obj_fun1函数来计算适应度

（这里写成x(i,:)主要是为了和以后遇到的多元函数互通）

end

pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）

ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标

gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

function y = Obj_fun1(x)

y = 11*sin(x) + 7*cos(5*x);

end

注释！！！：

（1）这里的适应度实际上就是

我们的目标函数值。

（2）这里可以直接计算出pbest

和gbest，在后面将用于计算粒子

的速度以更新粒子的位置。

循环体：更新粒子速度和位置

for d = 1:K % 开始迭代，一共迭代K次

for i = 1:n % 依次更新第i个粒子的速度与位置

% 更新第i个粒子的速度

v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));

% 如果粒子的速度超过了最大速度限制，就对其进行调整

for j = 1: narvs

if v(i,j) < -vmax(j)

v(i,j) = -vmax(j);

elseif v(i,j) > vmax(j)

v(i,j) = vmax(j);

end

end

x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置

% 如果粒子的位置超出了定义域，就对其进行调整

for j = 1: narvs

if x(i,j) < x_lb(j)

x(i,j) = x_lb(j);

elseif x(i,j) > x_ub(j)

x(i,j) = x_ub(j);

end

end

子程序：

重新计算适应度并找到最优粒子

fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度

% 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度

if fit(i) > Obj_fun1(pbest(i,:))

pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置

end

% 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度

if Obj_fun1(pbest(i,:)) > Obj_fun1(gbest)

gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置

end

end

end

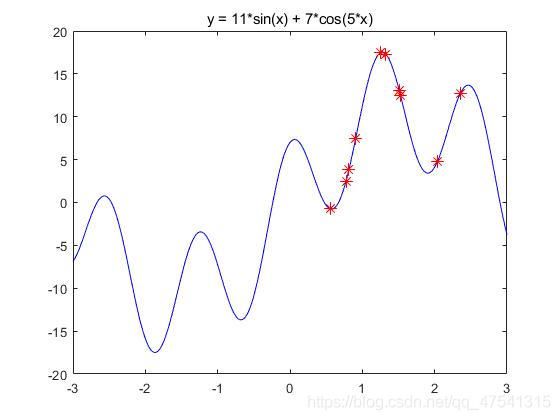
运算结果：

最佳的位置是：

    1.2754

此时最优值是：

   17.4928

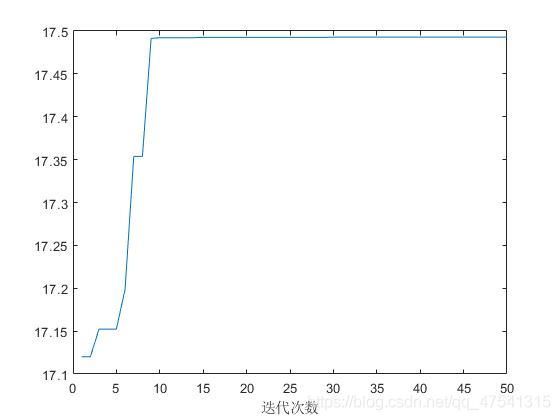
迭代图：

 

具体代码：

main

%% 粒子群算法PSO
clear; clc
%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 50;  % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界

%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs);  % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）

%% 计算适应度
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun1(x(i,:));   % 调用Obj_fun1函数来计算适应度（这里写成x(i,:)主要是为了和以后遇到的多元函数互通）
end
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1);  % 找到适应度最大的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun1(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) > Obj_fun1(pbest(i,:))   % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) > Obj_fun1(gbest)  % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun1(gbest);  % 更新第d次迭代得到的最佳的适应度
%     pause(0.1)  % 暂停0.1s
%     h.XData = x;  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
%     h.YData = fit; % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
end

figure(2)
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun1(gbest))

Obj_fun1

function y = Obj_fun1(x)
    y = 11*sin(x) + 7*cos(5*x);
    %    y = -(11*sin(x) + 7*cos(5*x));  % 如果调用fmincon函数，则需要添加负号改为求最小值
end