【大画数据结构】第一话 —— 动态顺序表的增删改查

---

什么是线性表

在学习 顺序表 之前，我们先要了解一下 线性表。

线性表，从名字上你就能感觉到，是具有像线一样的性质的表。

举个例子：

一个班级的小朋友，一个跟着一个排着队，有一个打头，有一个收尾，当中的小朋友每一个都知道他前面一个是谁，他后面一个是谁，这样如同有一根线把他们串联起来了。就可以称之为 线性表。

线性表（List）：零个或多个数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串…

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以 数组 和 链式结构 的形式存储。

今天我们将要学习的是线性表的两种物理结构的第一种：顺序存储结构。

什么是顺序表

顺序表 就是：线性表的顺序存储结构，指的是 用一段地址连续的存储单元依次存储线性表的数据元素。

说白了，就是在内存中找了块地儿，通过占位的形式，把一定内存空间给占了，然后把 相同数据类型的数据元素依次存放在这块空地中。

既然线性表的每个数据元素的类型都相同，所以可以用 C 语言的一维数组来实现顺序存储结构，即把第一个数据元素存到数组下标为 0 的位置中，接着把线性表相邻的元素存储在数组中相邻的位置。

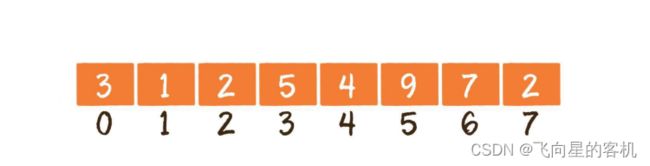
我们知道内存是由⼀个个连续的内存单元组成的，每⼀个内存单元都有⾃⼰的地址。在这些内存单元中，有些被其他数据占⽤了，有些是空闲的。

数组中的每⼀个元素，都存储在⼩⼩的内存单元中，并且元素之间紧密排列，既不能打乱元素的存储顺序，也不能跳过某个存储单元进⾏存储。

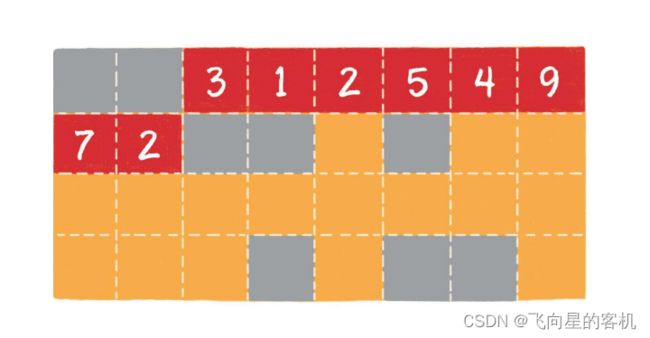
在上图中，橙⾊ 的格⼦代表 空闲 的存储单元，灰⾊ 的格⼦代表 已占⽤ 的存储单元，⽽ 红⾊ 的连续格⼦代表 数组在内存中的位置。

总结：

顺序表就是数组，但是再数组的基础上，它还要求数据是连续存储的，不能跳跃间隔。

顺序表的分类

既然顺序表也是用 数组 来存储的，那么它和 数组 的区别在哪里呢？
 
（1）普通数组的长度是固定的，而顺序表的长度可以动态增长；
 
（2）普通数组的数据存放可以不连续，而顺序表要求插入的数据在内存中是连续的；

我们来先看长度固定的顺序表，也就是 静态顺序表

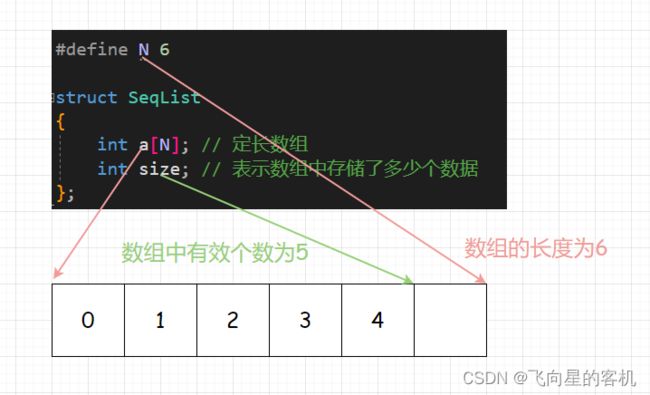
静态顺序表 的特点：如果存满了就不让插入，现在N 是 6，假设我要存 10 个数呢？所以 N 给小了不够用，N 给大了就存在浪费；

我们再来看下 动态顺序表；

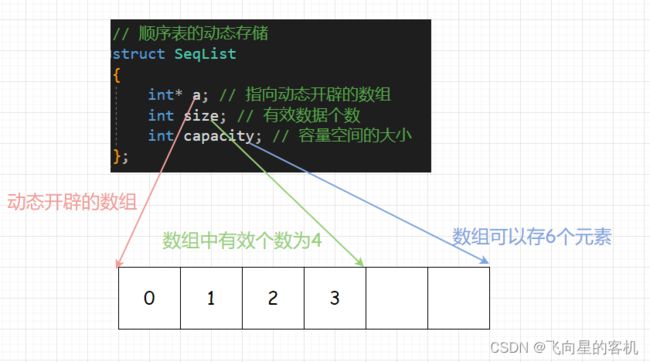
a： 是一个指针，指向动态开辟的这块儿空间；

size： 表示数组中存储了多少个数据；

capacity： 表示数组实际能存数据的空间容量是多大；

1. 初始化顺序表

首先，我们要创建一个 顺序表 类型，该顺序表类型包括了 顺序表的起始位置、记录 顺序表内有效数据个数（size），以及记录 当前顺序表的容量（capacity）。

typedef int SLDataType;

typedef struct SeqList
{
	// 要用指针a 去指向动态开辟的那一块儿空间
	SLDataType* a; // 声明了一个指向顺序表的指针，称它为 "顺序表指针"
	int size; // 记录当前顺序表内元素个数
	int capacity; // 记录当前顺序表的最大容量（容量个数）
}SeqList;

然后，我们需要一个初始化函数，对顺序表进行初始化。

//初始化顺序表
void SeqListInit(SeqList* ps) {
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

2. 销毁顺序表

因为我们的 顺序表 是使用 动态内存开辟 的，所以使用完以后，一定要释放，防止内存泄漏。

//顺序表销毁
void SeqListDestroy(SeqList* ps) {
	free(ps->a);
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

3. 打印顺序表

这个很简单，直接用 循环 依次打印 顺序表 内的元素个数就好了。

//打印顺序表
void SeqListPrint(SeqList* ps) {
	int i = 0;
	for (i = 0; i < ps->size; ++i) {
		printf("%d ", ps->a[i]);
	}
	printf("\n");
}

4. 插入数据

在 顺序表 中插入数据的方法有三种，分别是：
 
（1）在 顺序表 头部插入数据；
 
（2）在 顺序表 尾部插入数据；
 
（3）在 顺序表 任意 下标（数组的下标是从 0 开始的） 位置插入数据；

动图演示

但是在插入数据之前，我们来思考一个问题：

代码中的成员变量 size 是数组实际元素的数量。如果插⼊元素在数组尾部，传⼊的下标参数 index 等于 size；
 
如果插⼊元素在数组中间或头部，则 index ⼩于 size。
 
如果传⼊的下标参数 index ⼤于 size 或 ⼩于 0，则认为是⾮法输⼊，会直接抛出异常。
 
可是，如果数组不断插⼊新的元素，元素数量超过了数组的最⼤⻓度，数组岂不是要 “撑爆” 了？
 
这就是接下来要讲的情况 —— 扩容顺序表。

扩容顺序表

为什么要扩容呢？

首先，我们每次在 顺序表 里面增加数据时，都应该先检查 顺序表内元素个数是否已达到顺序表容量上限，什么意思呢？

假如现在有⼀个⻓度为 6 的数组，已经装满了元素，这时还想插⼊⼀个新元素，如图所示

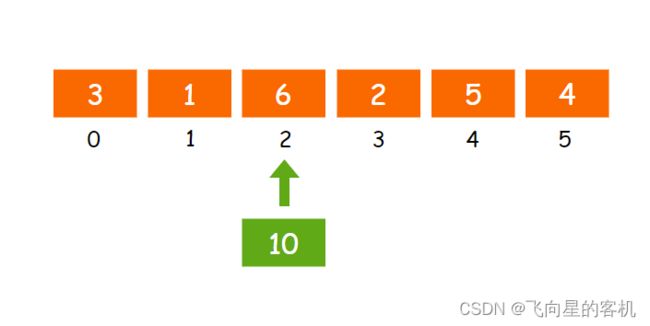
这就涉及数组的扩容了。我们可以使用 realloc 对数组进行动态扩容，把旧数组在其原有的容量上，扩充 2 倍，这样就实现了数组的动态扩容。

为什么要使用 realloc，而不使用 malloc 呢？

因为：若传入 realloc 的指针为空指针（NULL），则 realloc 函数的作用等同于 malloc 函数。

代码示例

//插入数据之前，先扩容顺序表
void SeqListCheckCapacity(SeqList* ps) {
	// /当 size 和 capacity 相等的时候，就进行扩容
	if (ps->size == ps->capacity) {
		int newcapacity = (ps->capacity == 0) ? (4) : (ps->capacity * 2);
		SLDataType* tmp = (SLDataType*)realloc(ps->a, newcapacity * sizeof(SLDataType));
		if (tmp == NULL) {
			printf("realloc fail\n"); // 开辟就退出来
			exit(-1); // 如果失败了，就直接终止程序；正常是0；
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
}

假设把 capacity 的初始值设置为 0 个：

(ps->capacity == 0) ? (4) : (ps->capacity * 2)：则 capacity 第一次进行判断等于 0，那么直接就开 4 个；

当 4 个空间用完了以后，capacity 第二次进来不等于 0，那么就乘以 2 倍，从 4 个扩容到 8 个；

头插

假设有下面一个 顺序表，我想要在 头部，也就是 下标为 0 的起始位置插入一个数字 8，该如何实现呢？

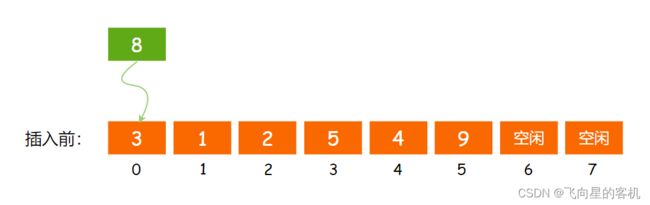
很简单，只需要先将顺序表 原有的数据 从后往前 依次向后挪动一位，最后再将数字 8 插入表头，如图所示

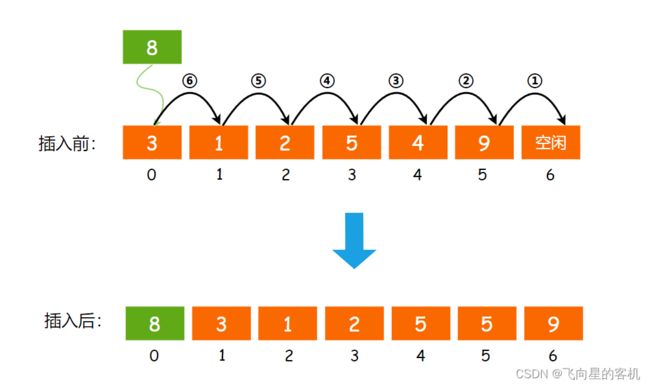
但是我们还要考虑一个点，就是如果没有多余的空间呢？也就是 元素个数（size）和 数据容量（capacity）相等了，如图所示

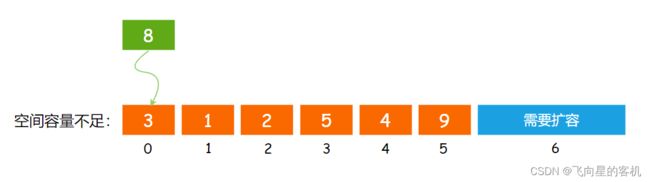
这种情况就不能向后挪动，所以在挪动之前要先检查 顺序表 的容量是否足够，不够就需要进行扩容

代码示例

//头插
void SeqListPushFront(SeqList* ps, SLDataType x) {
	assert(ps);
	SeqListCheckCapacity(ps); // 检查容量
	int end = ps->size - 1;
	while (end >= 0) {
		ps->a[end + 1] = ps->a[end]; // 将数据 从后往前 依次 向后挪动
		--end;
	}
	ps->a[0] = x;
	ps->size++; // 插入完以后，顺序表元素个数加一
}

注意： 挪动数据的时候应 从后向前 依次挪动，若从前向后挪动，会导致后一个数据被覆盖。

尾插

尾插 相对于 头插 就比较简单了.

假设有下面一个 顺序表，我想要在 尾部，也就是 下标为 6 的 结束位置 插入一个数字 8，该如何实现呢？如图所示

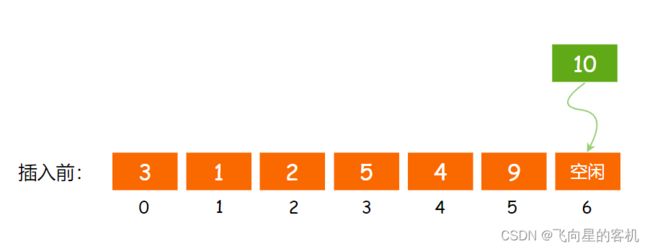
很简单，首先 检查容量是否足够，如果不够，先扩容；如果够，直接在 顺序表尾部 插入数据即可，如图所示

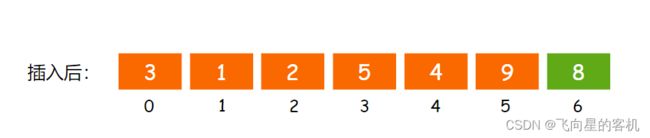
代码示例

//尾插
void SeqListPushBack(SeqList* ps, SLDataType x) {
	assert(ps);
	SeqListCheckCapacity(ps); // 检查容量
	ps->a[ps->size] = x;
	ps->size++; // 插入完以后，顺序表元素个数加一
}

指定下标位置插入

在 顺序表 里，如果要 中间插入，稍微复杂一些。

由于数组的每⼀个元素都有其固定下标，所以不得不⾸先把插⼊位置及后⾯的元素向后移动，腾出地⽅，再把要插⼊的元素放到对应的数组位置上

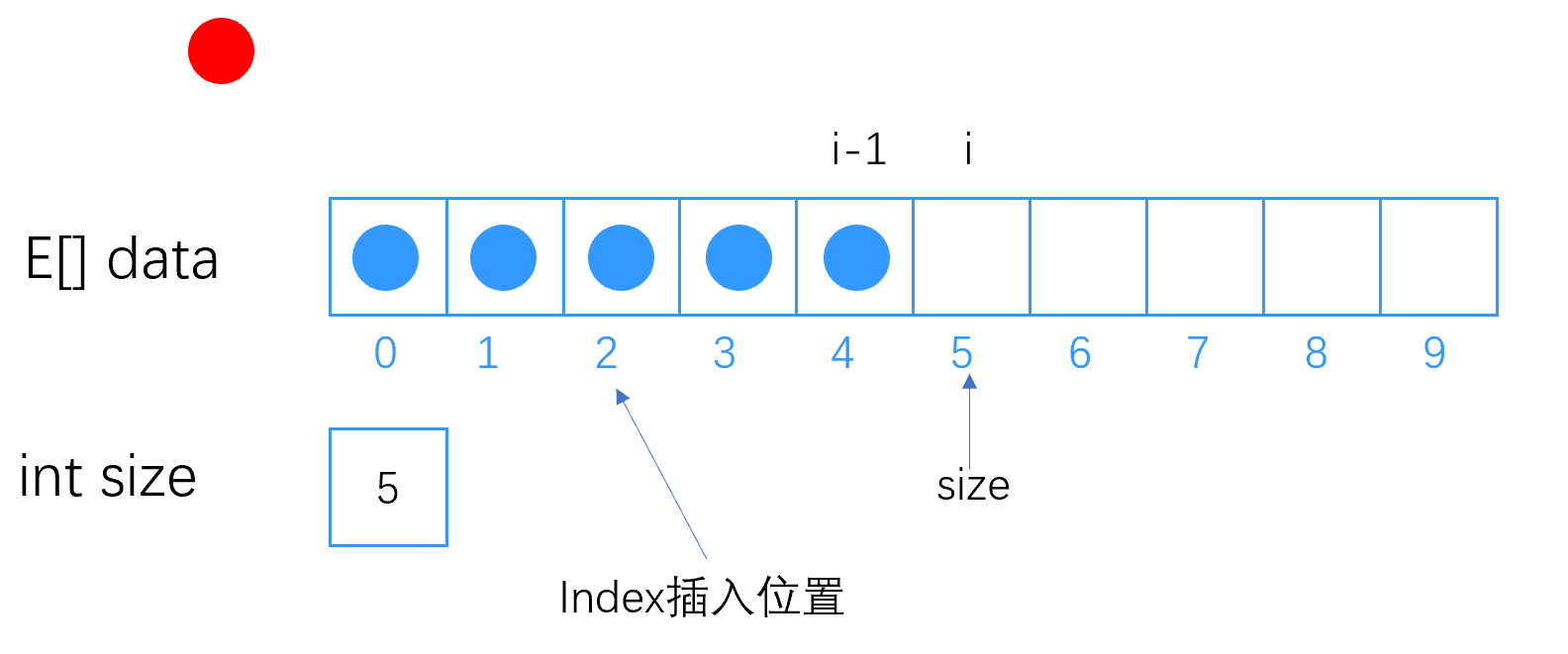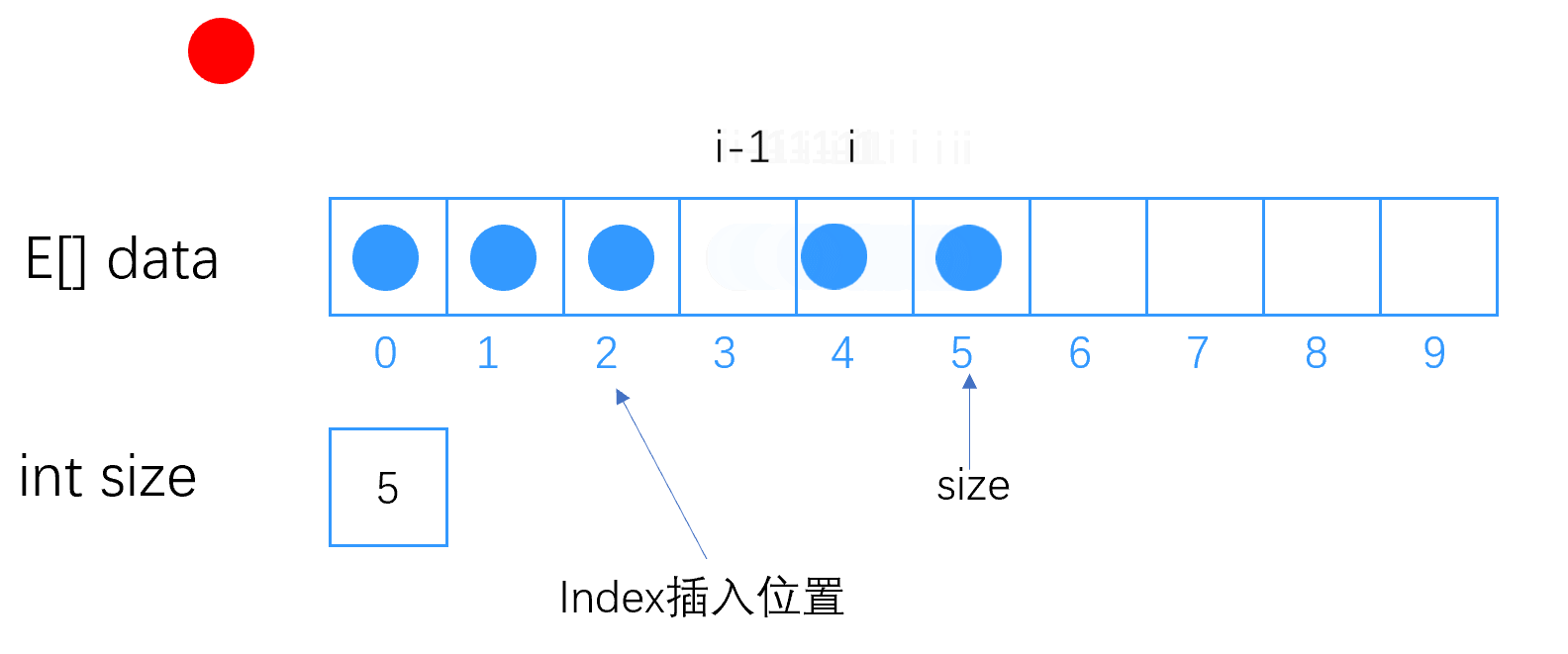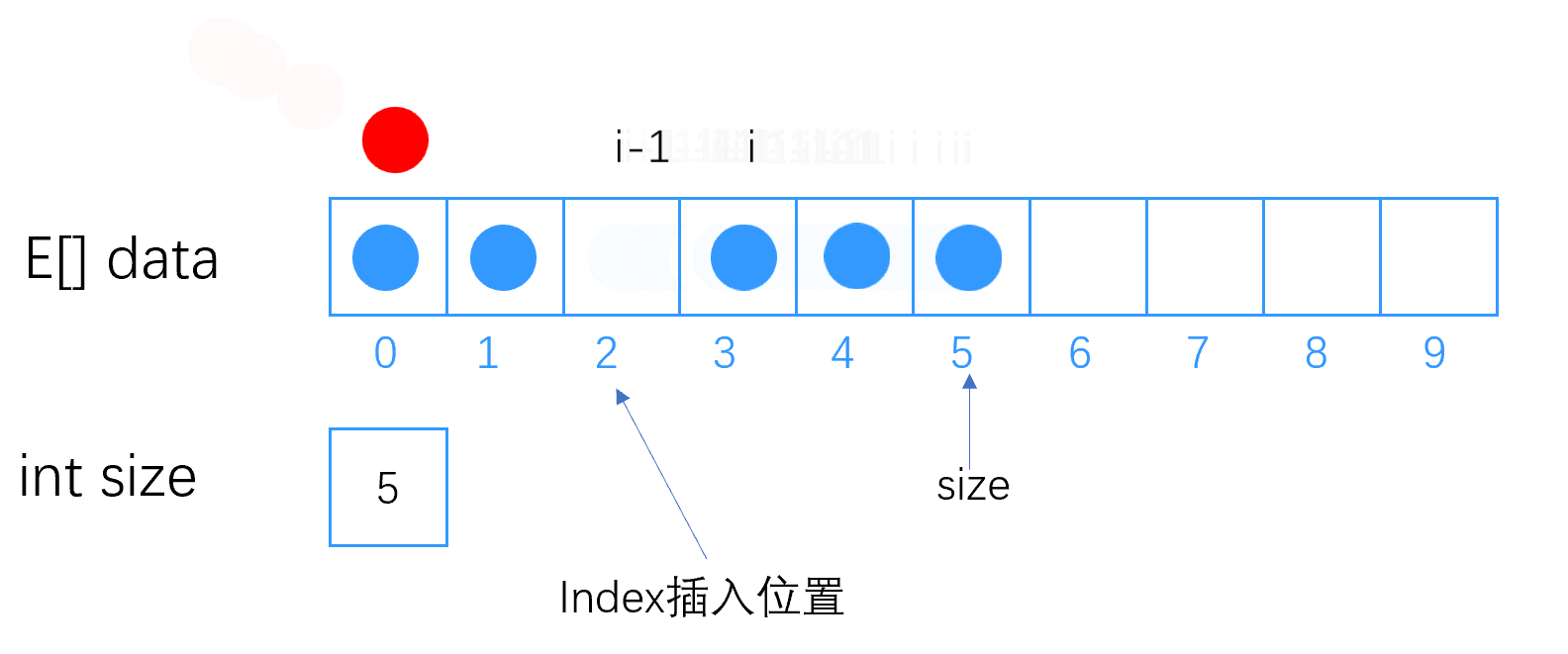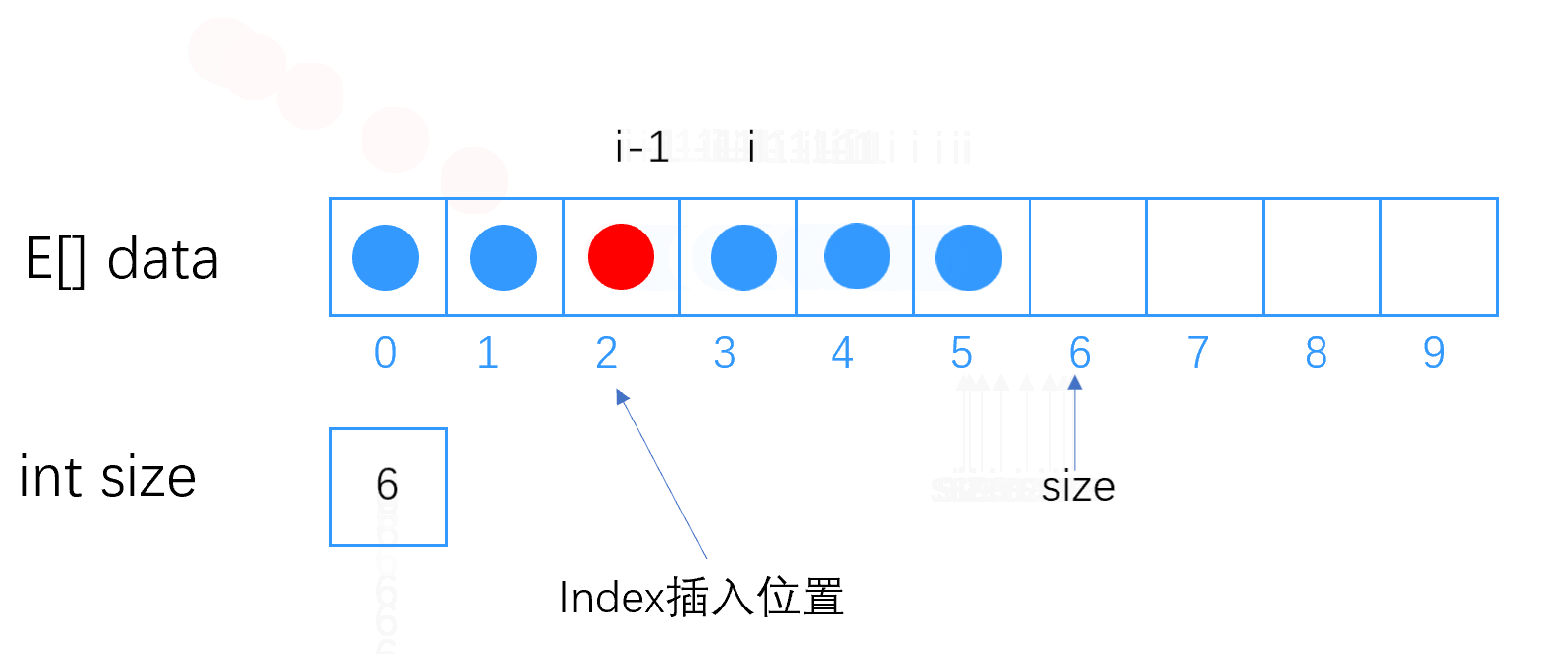
假设我们要把数字 10 插入到 下标（pos） 为 2 的位置，如图所示

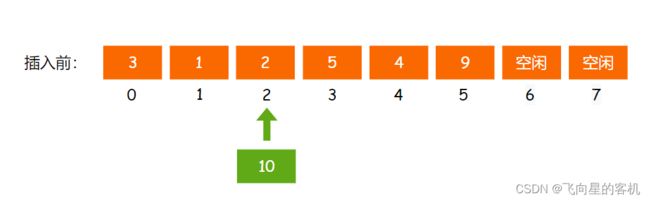
首先从该 下标 位置开始（包括该位置的元素），把其后的元素依次 向后挪动一位 ，如图所示

最后将元素 10 插入到下标 2 的位置，如图所示

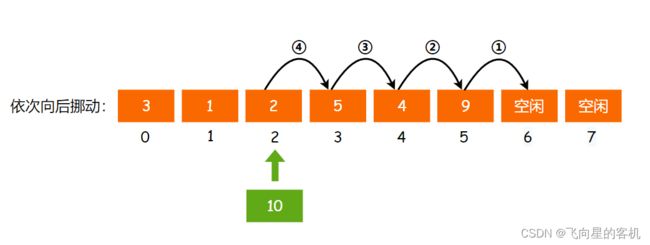
注意：插入前还是先判断顺序表尾部是否足够的空间，没有的话，需要扩容

代码示例

//顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, int pos, SLDataType x) {
	assert(pos >= 0 && pos <= ps->size); // 检查输入下标的合法性
	SeqListCheckCapacity(ps); // 检查容量
	int end = ps->size - 1;
	while (end >= pos) {
		ps->a[end + 1] = ps->a[end]; // 从pos下标位置开始，其后的数据依次向后挪动
		--end;
	}
	ps->a[pos] = x; // 再pos位置插入x
	ps->size++; // 顺序表元素个数加一
}

代码优化

我们可以发现：

头插 实际上就是在顺序表 下标为 0 的位置插入数据；

尾插 实际上就是在顺序表 下标为 ps->size 的位置插入数据；

那么就意味着我们可以统一使用上面的 SeqListInsert 函数来实现头插和尾插。

代码示例

// 头插
void SeqListPushFront(SeqList* ps, SLDataType x)
{
	SeqListInsert(ps, 0, x); // 在下标为0的位置插入数据
}

// 尾插
void SeqListPushBack(SeqList* ps, SLDataType x)
{
	SeqListInsert(ps, ps->size, x); // 在下标为 ps->size 的位置插入数据
}

5. 删除数据

数组的删除操作和插⼊操作的过程相反：
 
如果删除的元素位于顺序表头部，其后的元素都需要向前挪动 1 位。
 
如果删除的元素位于顺序表中间，其后的元素都需要向前挪动 1 位。
 
如果删除的元素位于顺序表尾部，直接将顺序表的元素个数减 1 位。

头删

要删除顺序表头部的数据，我们可以从下标为 1 的位置开始，依次将数据 向前覆盖 即可，如图所示

代码示例

//头删
void SeqListPopFront(SeqList* ps) {
	assert(ps);
	assert(ps->size > 0); // 保证顺序表不为空
	int begin = 1;
	while (begin < ps->size) {
		ps->a[begin-1] = ps->a[begin]; // 将数据依次向前覆盖
		++begin;
	}
	ps->size--; // 顺序表元素个数减一
}

尾删

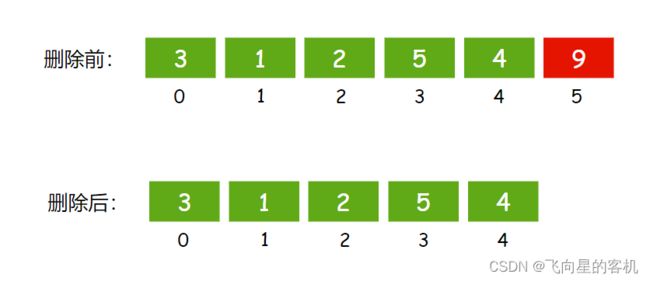
从顺序表 尾部 删除数据的话，就更简单了，因为我们的顺序表是动态内存开辟的，所以直接将 顺序表的元素个数减一 即可。如图所示

代码示例

//尾删
void SeqListPopBack(SeqList* ps) {
	assert(ps);
	assert(ps->size > 0); // 如果条件为真，那么就没事；如果条件为假，那么就终止掉程序
	ps->size--; // 顺序表元素个数减一
}

指定下标位置删除

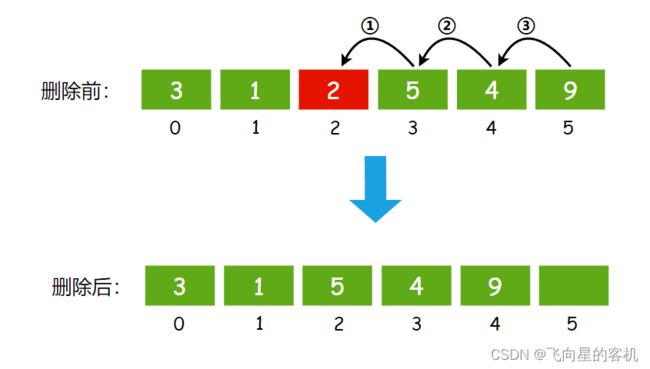
如果删除的元素位于数组中间，其后的元素依次 向前覆盖 即可。如图所示

代码示例

//顺序表删除在pos位置的值
void SeqListErase(SeqList* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos < ps->size); // 保证顺序表不为空
	int begin = pos + 1;
	while (begin < ps->size) {
		ps->a[begin - 1] = ps->a[begin]; // 从pos下标位置开始，其后的数据从前往后依次向前覆盖
		++begin;
	}
	ps->size--;
}

代码优化

同 头插 一样，我们可以发现：

头删 实际上就是在顺序表 下标为 0 的位置删除数据；

尾删 实际上就是在顺序表 下标为 ps->size 的位置删除数据；

那么就意味着我们可以统一使用上面的 SeqListErase 函数来实现头删和尾删。

代码示例

//头删
void SeqListPopFront(SeqList* ps)
{
	SeqListErase(ps, 0); // 删除下标为0的位置的数据
}

//尾删
void SeqListPopBack(SeqList* ps)
{
	SeqListErase(ps, ps->size - 1); // 删除下标为ps->size - 1的位置的数据
}

6. 查找数据

假设我们要查找顺序表内的某个数，怎么办呢？

很简单，直接遍历一次顺序表即可，若找到了目标数据，则停止遍历，并返回该数据的下标；找不到，就返回 -1。

代码示例

//顺序表查找
int SeqListFind(SeqList* ps, SLDataType x) {
	// 遍历顺序表进行查找
	for (int i = 0; i < ps->size; ++i) {
		if (ps->a[i] == x) {
			return i; // 找到该数据，返回下标
		}
	}
	return -1; // 未找到，返回-1
}

7. 修改数据

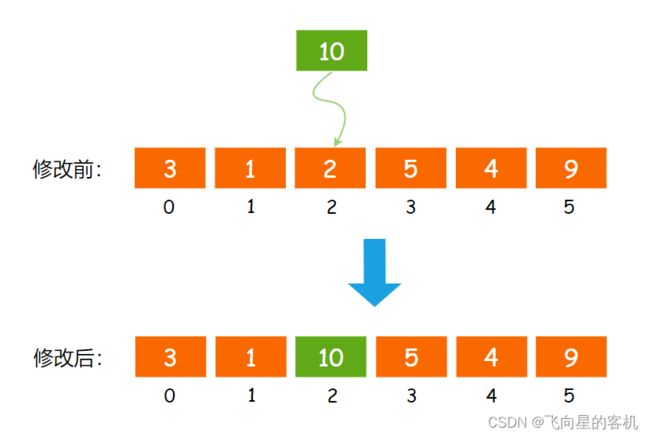
假设我们要对顺序表内的某个元素进行修改呢？

也很简单，直接对该位置的数据进行再次赋值即可，如图所示

代码示例

//顺序表修改在pos位置的数据
void SeqListModify(SeqList* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos < ps->size);//检查输入下标的合法性
	ps->a[pos] = x; // 直接修改数据
}

8. 总结

那么顺序表的 插⼊和 删除 操作，时间复杂度分别是多少？

插入： 数组扩容的时间复杂度是 $O(n)$，插⼊并移动元素的时间复杂度也是 $O(n)$，综合起来插⼊操作的时间复杂度是 $O(n)$ 。
 
删除： ⾄于删除操作，只涉及元素的移动，时间复杂度也是 $O(n)$。

9. 接口函数贴图

最后附上一张完整的 顺序表 的 接口函数图